[개념] 신호처리 및 푸리에 변환

원본 게시글: https://velog.io/@euisuk-chung/신호처리-및-푸리에-변환

신호처리란?

신호처리(Signal Processing)는 신호를 분석하고 변환하며 해석하는 기술과 방법을 연구하는 학문입니다. 신호는 시간에 따라 변화하는 물리량이나 데이터로, 음성, 영상, 전기 신호, 생체 신호 등 다양한 형태로 존재할 수 있습니다. 신호처리의 목적은 이러한 신호로부터 유용한 정보를 추출하거나 신호를 변형하여 특정 목적을 달성하는 것입니다.

신호처리의 목적

1. 신호 분석 (Signal Analysis):

   • 신호의 특성을 분석하고 이해합니다. 예를 들어, 음성 신호의 주파수 성분을 분석하여 음성 인식을 수행하거나, ECG 신호를 분석하여 심장 상태를 평가합니다.

2. 신호 변환 (Signal Transformation):

   • 신호를 다른 형태로 변환하여 보다 쉽게 분석하거나, 원하는 정보만 추출할 수 있도록 합니다. 예를 들어, 시간 도메인 신호를 주파수 도메인으로 변환하는 푸리에 변환이 있습니다.

3. 신호 복원 (Signal Reconstruction):

   • 손상된 신호를 복원하거나, 노이즈가 포함된 신호에서 원래의 신호를 재구성합니다. 예를 들어, 잡음이 포함된 음성 신호에서 잡음을 제거하고 원래의 음성을 복원합니다.

4. 신호 압축 (Signal Compression):

   • 신호의 데이터 양을 줄여 저장 공간을 절약하거나 전송 속도를 높입니다. 예를 들어, JPEG나 MP3와 같은 데이터 압축 기술이 있습니다.

5. 신호 필터링 (Signal Filtering):

   • 원치 않는 성분이나 노이즈를 제거하여 신호를 정제합니다. 예를 들어, ECG 신호에서 고주파 노이즈를 제거하여 심장 박동 패턴을 명확히 합니다.

신호처리의 응용 분야

신호처리는 다양한 분야에 걸쳐 널리 응용됩니다. 주요 응용 분야는 다음과 같습니다:

1. 통신 (Telecommunications):

   • 데이터 전송, 압축, 오류 수정 등을 통해 효율적인 정보 전달을 보장합니다. 예를 들어, 휴대폰 통화, 인터넷 데이터 전송 등이 포함됩니다.

2. 의료 (Medical):

   • 의료 영상 처리, 생체 신호 분석 등을 통해 진단과 치료를 지원합니다. 예를 들어, MRI 이미지 처리, ECG 신호 분석 등이 있습니다.

3. 오디오 및 음성 처리 (Audio and Speech Processing):

   • 음성 인식, 음성 합성, 음악 신호 처리 등을 포함합니다. 예를 들어, 스마트폰의 음성 인식 기능, 음악 스트리밍 서비스 등이 있습니다.

4. 영상 및 비디오 처리 (Image and Video Processing):

   • 이미지 필터링, 얼굴 인식, 비디오 압축 등을 포함합니다. 예를 들어, 디지털 카메라의 이미지 개선, CCTV 영상 분석 등이 있습니다.

5. 레이다 및 센서 시스템 (Radar and Sensor Systems):

   • 레이다 신호 분석, 센서 데이터 처리 등을 통해 환경 감지 및 제어를 수행합니다. 예를 들어, 자동차의 자율 주행 시스템, 기상 레이다 등이 있습니다.

푸리에 변환

푸리에 변환(Fourier Transform)은 신호를 여러 개의 정현파(sinusoidal waves)로 분해하는 수학적 (변환, transformation) 기법입니다. 이를 이해하기 위해 기본적인 신호 처리와 파형에 대한 용어를 먼저 간단하게 소개하겠습니다.

용어 정리

1. 신호 (Signal)

• 푸리에 변환에도 마찬가지로 신호가 들어오 됩니다. 신호는 시간에 따라 변하는 데이터입니다. 예를 들어, 음성 신호, 온도 변화 데이터, 주식 가격 등이 있습니다.

2. 정현파 (Sinusoidal Wave)

• 정현파는 사인 함수나 코사인 함수로 표현되는 파형으로, 주기적이고 규칙적인 형태를 가집니다. 이는 수학적으로는 아래와 같이 표현될 수 있습니다.:

f(t)=A⋅sin⁡(2πft+ϕ) f(t) = A \cdot \sin(2\pi ft + \phi) f(t)=A⋅sin(2πft+ϕ) 

• A는 진폭(Amplitude)으로, 파형의 최대 높이입니다.
• f는 주파수(Frequency)로, 파형이 1초에 몇 번 진동하는지를 나타냅니다.
• t는 시간(Time)입니다.
• ϕ\phiϕ는 위상(Phase)으로, 파형이 시간 축을 기준으로 얼마나 이동했는지를 나타냅니다.

푸리에 변환의 원리

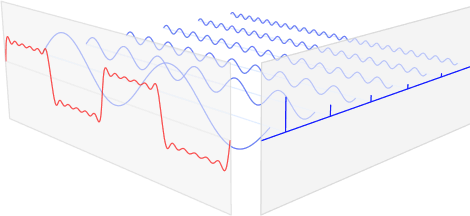
그림 1. 푸리에 변환 (출처: 위키피디아)

1. 신호의 분해

푸리에 변환은 복잡한 신호를 다양한 주파수를 가지는 여러 개의 정현파로 분해합니다. 이 과정은 다음과 같은 원리를 따릅니다:

• 임의의 주기적인 신호는 여러 개의 정현파의 합으로 표현될 수 있습니다.
• 각 정현파는 특정 주파수, 진폭, 위상을 가집니다.

2. 수학적 표현

푸리에 변환은 시간 도메인에서 주파수 도메인으로 변환하는 수학적 도구입니다. 이를 통해 신호를 구성하는 각 주파수 성분의 크기와 위상을 얻을 수 있습니다.

• 주어진 시간 신호 x(t)x(t)x(t)에 대해 푸리에 변환은 다음과 같이 정의됩니다:

X(f)=∫−∞∞x(t)⋅e−j2πft dt X(f) = \int_{-\infty}^{\infty} x(t) \cdot e^{-j2\pi ft} \, dt X(f)=∫−∞∞​x(t)⋅e−j2πftdt 

• x(f)x(f)x(f)는 주파수 fff에서의 푸리에 변환 결과입니다.
• x(t)x(t)x(t)는 시간 도메인의 신호입니다.
• e−j2πfte^{-j2\pi ft}e−j2πft 는 복소수 지수 함수로, 사인과 코사인을 포함합니다.

이 수식은 신호 x(t)x(t)x(t)를 주파수 성분 fff 로 분해하는 과정입니다. X(f)X(f)X(f) 는 복소수로, 그 크기는 해당 주파수 성분의 진폭을, 위상은 해당 주파수 성분의 위상을 나타냅니다.

• 입력신호 X(f)X(f)X(f)가 e−j2πfte^{-j2πft}e−j2πft들의 합(적분)으로 표현(분해)된다는 의미와 동일하게 됩니다.

💡 (참고) e−j2πfte^{-j2πft}e−j2πft가 뭡니까??

✍️ 오일러 공식(Euler’s formula)은 복소지수함수를 삼각함수로 변환할 수 있도록 합니다. 이러한 오일러 공식을 활용하면, X(f)=∫−∞∞x(t)⋅e−j2πft dt X(f) = \int_{-\infty}^{\infty} x(t) \cdot e^{-j2\pi ft} \, dt X(f)=∫−∞∞​x(t)⋅e−j2πftdt  의 실수부가 cos(2πux), 허수부가 sin(2πux)인 주기함수임을 알 수 있습니다.

💡 (참고) 오일러 공식은 어떻게 정의합니까?

✍️ ejθ=cos⁡(θ)+jsin⁡(θ)e^{j \theta}=\cos (\theta)+j \sin (\theta)ejθ=cos(θ)+jsin(θ)

• eee는 자연상수, j는 허수단위로, j2=−1j^2=-1j2=−1을 만족하고, θ\thetaθ는 각도를 의미함
• 따라서 위의 오일러공식에서 실수부, 허수부는 각각 cos(θ)cos(\theta)cos(θ), sin(θ)sin(\theta)sin(θ)를 의미함

푸리에 변환에서의 오일러 공식 적용하면?

• 푸리에 변환에서 신호 x(t)x(t)x(t) 의 주파수 성분을 구할 때 사용하는 식은 다음과 같습니다:

X(f)=∫−∞∞x(t)⋅ej2πftdtX(f)=\int_{-\infty}^{\infty} x(t) \cdot e^{j 2 \pi f t} d tX(f)=∫−∞∞​x(t)⋅ej2πftdt

• 여기서 ej2πfte^{j 2 \pi f t}ej2πft 를 오일러 공식을 이용해 풀면 다음과 같이 됩니다:

ej2πft=cos⁡(2πft)−jsin⁡(2πft)e^{j 2 \pi f t}=\cos (2 \pi f t)-j \sin (2 \pi f t)ej2πft=cos(2πft)−jsin(2πft)

• 따라서, 푸리에 변환 식을 다시 쓰면:

X(f)=∫−∞∞x(t)⋅(cos⁡(2πft)−jsin⁡(2πft))dtX(f)=\int_{-\infty}^{\infty} x(t) \cdot(\cos (2 \pi f t)-j \sin (2 \pi f t)) d tX(f)=∫−∞∞​x(t)⋅(cos(2πft)−jsin(2πft))dt

이를 각각 실수부와 허수부로 나누어 표현할 수 있습니다:

• 실수부: ∫∞∞x(t)⋅cos⁡(2πft)dt\int_{\infty}^{\infty} x(t) \cdot \cos (2 \pi f t) d t∫∞∞​x(t)⋅cos(2πft)dt
• 허수부: −j∫∞∞x(t)⋅sin⁡(2πft)dt-j \int_{\infty}^{\infty} x(t) \cdot \sin (2 \pi f t) d t−j∫∞∞​x(t)⋅sin(2πft)dt

이제 이를 통해 푸리에 변환이 어떻게 동작하는지 직관적으로 이해할 수 있습니다:

1. 실수부 계산: 신호 x(t)x(t)x(t) 와 코사인 함수 cos⁡(2πft)\cos (2 \pi f t)cos(2πft) 의 내적(inner product)을 계산합니다. 이는 신호의 주파수 성분이 코사인 함수와 얼마나 일치하는지를 나타냅니다.
2. 허수부 계산: 신호 x(t)x(t)x(t) 와 사인 함수 sin⁡(2πft)\sin (2 \pi f t)sin(2πft) 의 내적을 계산하고, 이를 음 수로 만듭니다. 이는 신호의 주파수 성분이 사인 함수와 얼마나 일치하는지를 나타냅니다.

푸리에 변환 X(f)X(f)X(f) 는 이러한 실수부와 허수부를 합쳐서 표현됩니다. 이는 주어진 주파수 fff 에서 신호가 가지는 주파수 성분의 진폭와 위상을 나타냅니다.

3. 진폭과 위상 구하기

푸리에 변환의 복소수 표현

푸리에 변환의 결과 X(f)X(f)X(f) 는 일반적으로 복소수로 표현됩니다:

X(f)=A(f)ejϕ(f)X(f)=A(f) e^{j \phi(f)}X(f)=A(f)ejϕ(f)

여기서:

• A(f)A(f)A(f) 는 주파수 fff 에서의 진폭(Amplitude)입니다.
• ϕ(f)\phi(f)ϕ(f) 는 주파수 fff 에서의 위상(Phase)입니다.
• jjj 는 허수 단위로, j2=−1j^2=-1j2=−1 입니다.

복소수를 실수부와 허수부로 나누어 표현하면:

X(f)=Re⁡(X(f))+j⋅Im⁡(X(f))X(f)=\operatorname{Re}(X(f))+j \cdot \operatorname{Im}(X(f))X(f)=Re(X(f))+j⋅Im(X(f))

여기서:

• Re⁡(X(f))\operatorname{Re}(X(f))Re(X(f)) 는 실수부(Real part)입니다.
• Im⁡(X(f))\operatorname{Im}(X(f))Im(X(f)) 는 허수부(Imaginary part)입니다.

진폭과 위상 구하기

복소수 X(f)X(f)X(f) 에서 진폭과 위상을 구하는 방법은 다음과 같습니다:

1. 진폭(Amplitude)

진폭은 복소수 X(f)X(f)X(f) 의 크기(Magnitude)로, 피타고라스 정리를 사용하여 실수부 와 허수부로부터 계산할 수 있습니다:

2. 위상(Phase)

위상은 복소수 X(f)X(f)X(f) 의 각도(Angle)로, 아크탄젠트 함수(arc tangent function)를 사용하여 실수부와 허수부로부터 계산할 수 있습니다:

ϕ(f)=arg⁡(X(f))=tan⁡1(lm⁡(X(f))Rc⁡(X(f)))\phi(f)=\arg (X(f))=\tan ^1\left(\frac{\operatorname{lm}(X(f))}{\operatorname{Rc}(X(f))}\right)ϕ(f)=arg(X(f))=tan1(Rc(X(f))lm(X(f))​)

💡 (참고) 신호는 여러개의 정현파가 섞여있다고 하지 않았나요?

✍️ 네! 맞습니다. 여러 개의 정현파들이 섞인 신호는 다음과 같이 표현할 수 있습니다:

x(t)=A1cos⁡(2πf1t+ϕ1)+A2cos⁡(2πf2t+ϕ2)+…x(t)=A_1 \cos \left(2 \pi f_1 t+\phi_1\right)+A_2 \cos \left(2 \pi f_2 t+\phi_2\right)+\ldotsx(t)=A1​cos(2πf1​t+ϕ1​)+A2​cos(2πf2​t+ϕ2​)+…

• A1,A2,…A_1, A_2, \ldotsA1​,A2​,… 는 각 정현파의 진폭(Amplitude)입니다.
• f1,f2,…f_1, f_2, \ldotsf1​,f2​,… 는 각 정현파의 주파수(Frequency)입니다.
• ϕ1,ϕ2,…\phi_1, \phi_2, \ldotsϕ1​,ϕ2​,… 는 각 정현파의 위상(Phase)입니다.

4. 역 푸리에 변환 (Inverse Fourier Transform)

역 푸리에 변환은 주파수 도메인에서 시간 도메인으로 신호를 복원하는 과정입니다. 푸리에 변환이 신호를 주파수 성분으로 분해했다면, 역 푸리에 변환은 이 주파수 성분들을 다시 합쳐 원래의 시간 도메인 신호를 복원합니다.

• 수학적으로는 다음과 같이 표현됩니다:

x(t)=∫−∞∞X(f)⋅ej2πft dfx(t) = \int_{-\infty}^{\infty} X(f) \cdot e^{j2\pi ft} \, dfx(t)=∫−∞∞​X(f)⋅ej2πftdf

주파수 성분의 합성

역 푸리에 변환의 수식 x(t)=∫∞∞X(f)⋅ej2πftdfx(t)=\int_{\infty}^{\infty} X(f) \cdot e^{j 2 \pi f t} d fx(t)=∫∞∞​X(f)⋅ej2πftdf 는 각 주파수 성분 X(f)X(f)X(f) 와 해당 주파수의 정현파 ej2πfte^{j 2 \pi f t}ej2πft 의 곱을 적분하여 합치는 과정입니다.

이는 다음 과 같이 설명할 수 있습니다:

1. 각 주파수 성분 X(f)X(f)X(f):

   X(f)X(f)X(f) 는 주파수 fff 에서의 신호의 주파수 성분으로, 크기(진폭) ∣X(f)∣

   X(f)

   ∣X(f)∣ 와 위상 arg⁡(X(f))\arg (X(f))arg(X(f)) 로 구성됩니다.

2. 정현파 ej2πfte^{j 2 \pi f t}ej2πft :

   오일러 공식을 사용하여 ej2πfte^{j 2 \pi f t}ej2πft 는 코사인 함수와 사인 함수의 결합으로 표현됩니다:

ej2πft=cos⁡(2πft)+jsin⁡(2πft)e^{j 2 \pi f t}=\cos (2 \pi f t)+j \sin (2 \pi f t)ej2πft=cos(2πft)+jsin(2πft)

1. 곱셈:

   각 주파수 성분 X(f)X(f)X(f) 와 해당 주파수의 정현파 ej2πfte^{j 2 \pi f t}ej2πft 를 곱합니다. 이는 신호의 주파수 성분을 시간 도메인의 정현파로 변환하는 과정입니다.

2. 적분과 합성:

   모든 주파수 성분 fff 에 대해 이러한 곱셈을 적분하여 합치면, 원 래의 시간 도메인 신호 x(t)x(t)x(t) 가 복원될니다.

요약

1. 분해와 복원:

• 푸리에 변환은 시간 도메인 신호를 주파수 성분으로 분해하여 각 성분의 크기와 위상을 구합니다.
• 역 푸리에 변환은 이러한 주파수 성분들을 다시 시간 도메인으로 변환하 여 합치는 과정입니다.

1. 합성 과정:

• 각 주파수 성분 X(f)X(f)X(f) 는 해당 주파수의 정현파 ej2πfte^{j 2 \pi f t}ej2πft 와 곱해집니다.
• 이 곱셈은 각 주파수 성분이 원래 신호에 얼마나 기여하는지를 나타냅니 다.
• 모든 주파수 성분을 적분하여 합치면, 원래 신호가 복원됩니다.

예시 (Python 코드)

• 다음은 간단한 사인파 신호에 대해 푸리에 변환을 수행하는 Python 코드입니다:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np
import matplotlib.pyplot as plt

# 시간 도메인의 신호 생성
t = np.linspace(0, 1, 500)
x = np.sin(2 * np.pi * 1 * t)  # 1Hz 사인파

# 푸리에 변환 수행
X = np.fft.fft(x)
frequencies = np.fft.fftfreq(len(X), d=t[1] - t[0])

# 주파수 도메인의 신호 시각화
plt.figure(figsize=(12, 6))
plt.subplot(121)
plt.plot(t, x)
plt.title('Time Domain Signal')
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')

plt.subplot(122)
plt.stem(frequencies, np.abs(X), 'b', markerfmt=" ", basefmt="-b")
plt.title('Frequency Domain Signal')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Magnitude')

plt.tight_layout()
plt.show()

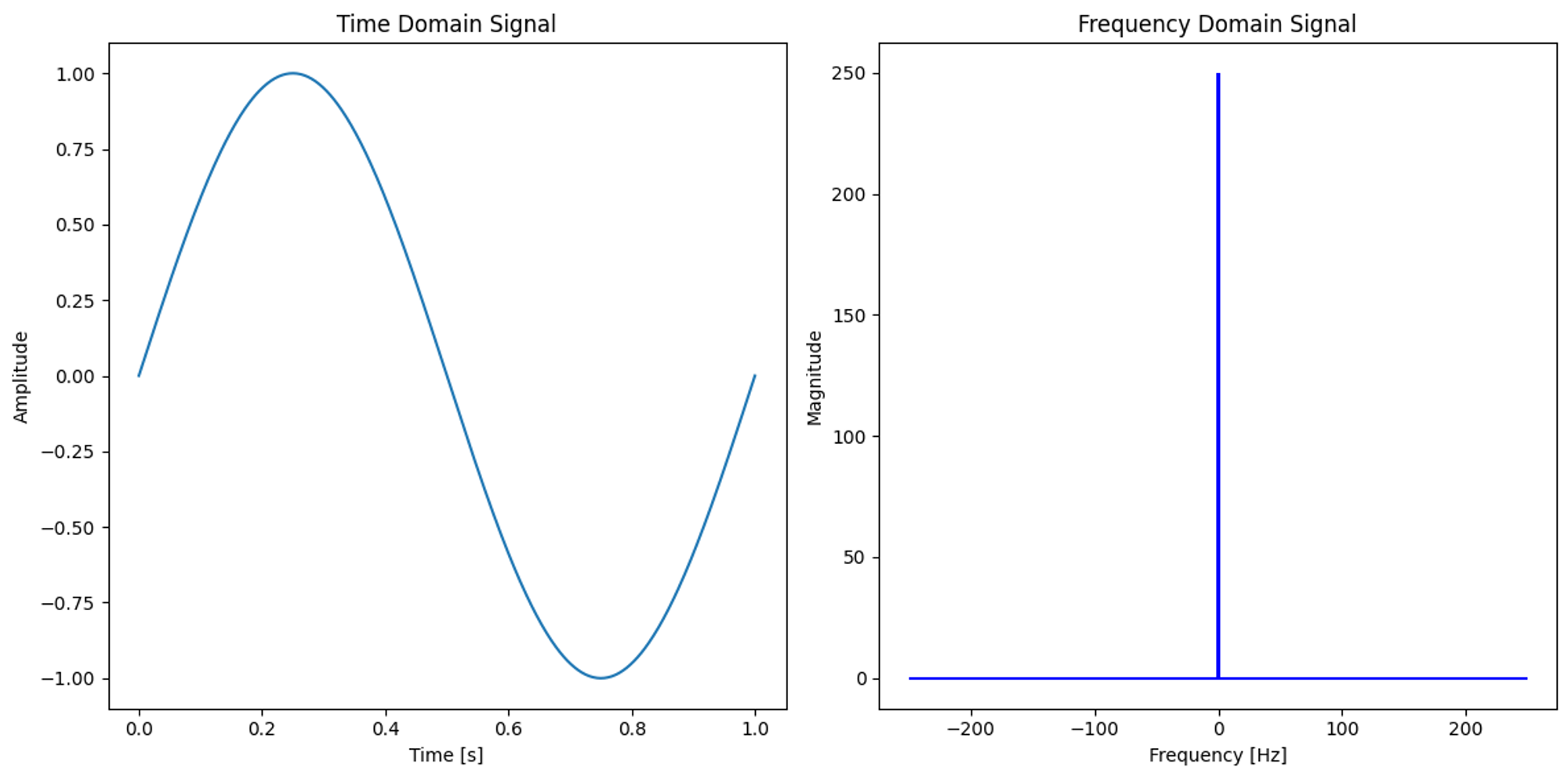
이 코드에서는 1Hz 사인파 신호를 생성하고, 이를 푸리에 변환하여 주파수 도메인에서 시각화합니다. 아래 그림을 확인해보시면, 주파수 도메인에서는 1Hz에서의 진폭이 크게 나타나는 것을 확인할 수 있습니다.

오늘도 제 포스트를 읽어주셔서 감사합니다 🥰

좋은 하루 ^~^

• Previous
  [꿀팁] Notion 단축키📖 (북마크 추천!!)
• Next
  [꿀팁] Confluence 단축키📖 (북마크 추천!!)