[머신러닝] 로지스틱 회귀 모델 (Logistic Regression)

1. 개요

안녕하세요! 이번 글에서는 머신러닝의 주요 개념인 로지스틱 회귀(Logistic Regression) 모델과 오즈 비(Odds Ratio)에 대해서 쉽게 정리해보았습니다. ~~친구에게 제대로 멋지게 설명하고 싶었는데, 뭔가 다시 한번 정리가 필요할 것 같더라고요 ㅎㅎ ^^7~~

로지스틱 회귀 모델은 범주형 데이터를 예측할 때 사용하는 통계적 방법으로, 특히 이진 분류 문제에서 많이 활용됩니다.
예를 들어, 특정 음식 소비 습관이 건강에 미치는 영향을 분석할 때 사용할 수 있습니다.

(참고) 본 블로그 포스트의 이미지 자료는 고려대학교 DMQA 김성범 교수님의 수업자료를 바탕으로 제작되었습니다.

💡 이진 분류 문제(Binary Classification Task) 란?

이진 분류는 집합 의 요소를 두 그룹(각각 클래스 라고 함) 중 하나로 분류하는 작업입니다. 일반적인 이진 분류 문제는 다음과 같습니다.

EX-1. 환자가 특정 질병을 앓고 있는지 아닌지를 판단하기 위한 건강검진.

EX-2. 정보 검색에서 페이지가 검색 결과 집합에 있어야 하는지 아닌지의 여부를 결정.

이 글에서는 오즈 비의 개념과 해석 방법을 먼저 설명한 후, 로지스틱 회귀 모델이 오즈 비를 활용하는 방식을 설명하겠습니다.

실험 데이터를 분석할 때 오즈 비를 응용하는 방법을 이해하는 데 많은 도움이 되길 바랍니다. 😜

2. 오즈 비(Odds Ratio)와 해석 방법

오즈 비(Odds Ratio, OR)는 두 그룹 간 특정 사건이 발생할 가능성을 비교하는 지표입니다.

연구에서 흔히 사용되는 오즈 비 해석 방법을 예제로 설명해보겠습니다.

예제: 음식 소비와 비만 간의 관계 분석

예를 들어 어떤 연구에서 고기 소비와 비만 간의 관계를 분석한다고 생각해봅시다.

연구자들은 200명의 참가자(N=200)를 대상으로 고기 소비량에 따라 두 그룹으로 나누었습니다.

그룹	비만 발생 (A)	비만 없음 (B)
고기 소비량 적음	30	70
고기 소비량 많음	50	50

이 데이터를 이용하여 오즈 비를 계산할 수 있습니다.

💡 잠깐! 오즈(Odds)란?

오즈(Odds)는 특정 사건이 발생할 확률을 발생하지 않을 확률로 나눈 값입니다. (뒤에서 더 자세하게 살펴보겠습니다)

발생할 확률발생하지 않을 확률\frac{\text{발생할 확률}}{\text{발생하지 않을 확률}}발생하지 않을 확률발생할 확률

고기 소비량이 적은 그룹에서 비만이 발생할 오즈(Odds):
- 비만 발생(A)을 사건(event)으로 보고, 비만이 발생할 확률과 발생하지 않을 확률의 비율을 계산합니다.

Odds Low Cosume =3070=0.43\text{Odds}_{\text{ Low Cosume }} = \frac{30}{70} = 0.43Odds Low Cosume =7030=0.43

고기 소비량이 많은 그룹에서 비만이 발생할 오즈(Odds):
- 비만 발생(A)을 사건(event)으로 보고, 비만이 발생할 확률과 발생하지 않을 확률의 비율을 계산합니다.

Odds High Cosume =5050=1\text{Odds}_{\text{ High Cosume }} = \frac{50}{50} = 1Odds High Cosume =5050=1

두 그룹의 오즈 비 계산:

OR=Odds High Cosume Odds Low Cosume=10.43≈2.33OR = \frac{\text{Odds}_{\text{ High Cosume }}}{\text{Odds}_{\text{ Low Cosume}}} = \frac{1}{0.43} \approx 2.33OR=Odds Low CosumeOdds High Cosume =0.431≈2.33

즉, 고기를 많이 소비하는 사람이 적게 소비하는 사람보다 비만이 발생할 확률이 약 2.33배 높다고 해석할 수 있습니다.

오즈 비(Odds Ratio, OR)

오즈 비(Odds Ratio, OR)는 두 개의 오즈(Odds)를 비교한 비율입니다. 이는 위아래의 순서에 따라 해석이 달라질 수 있습니다.

📌 오즈 비 계산에서 위아래 순서의 의미

오즈 비는 일반적으로 비교하고자 하는 그룹의 오즈를 분자로, 기준 그룹의 오즈를 분모로 놓고 계산합니다.

OR=Odds 비교 그룹Odds 기준 그룹OR = \frac{\text{Odds}_{\text{ 비교 그룹}}}{\text{Odds}_{\text{ 기준 그룹}}}OR=Odds 기준 그룹Odds 비교 그룹

OR > 1 : 비교 그룹에서 사건 발생 가능성이 기준 그룹보다 높음
OR < 1 : 비교 그룹에서 사건 발생 가능성이 기준 그룹보다 낮음
OR = 1 : 두 그룹 간 사건 발생 가능성에 차이가 없음

📌 현재 예제에서 적용

현재 예제에서는 고기 소비량이 많은 그룹을 비교 그룹, 고기 소비량이 적은 그룹을 기준 그룹으로 설정하였습니다.

OR=Odds고기 많이 소비Odds고기 적게 소비=1.00.43≈2.33OR = \frac{\text{Odds}_{\text{고기 많이 소비}}}{\text{Odds}_{\text{고기 적게 소비}}} = \frac{1.0}{0.43} \approx 2.33OR=Odds고기 적게 소비Odds고기 많이 소비=0.431.0≈2.33

즉, 고기를 많이 소비하는 그룹이 고기를 적게 소비하는 그룹보다 비만 발생 가능성이 2.33배 높다고 해석합니다.

🤔 만약 위아래를 바꾼다면?

만약 고기 소비량이 적은 그룹을 비교 그룹으로 하고 고기 소비량이 많은 그룹을 기준 그룹으로 놓는다면 다음과 같이 계산됩니다.

OR=Odds고기 적게 소비Odds고기 많이 소비=0.431.0≈0.43OR = \frac{\text{Odds}_{\text{고기 적게 소비}}}{\text{Odds}_{\text{고기 많이 소비}}} = \frac{0.43}{1.0} \approx 0.43OR=Odds고기 많이 소비Odds고기 적게 소비=1.00.43≈0.43

이 경우, 고기를 적게 소비하는 그룹이 고기를 많이 소비하는 그룹보다 비만 발생 가능성이 0.43배(즉, 낮다)라는 의미로 해석됩니다.

오즈 비의 크기는 동일하지만, 분모와 분자의 순서에 따라 해석이 달라질 수 있으므로, 연구 목적에 맞게 순서를 정하는 것이 중요합니다.
- 일반적으로 관심 있는 변수(예: 특정 행동을 했을 때의 효과)가 있는 그룹을 분자로 놓고 계산하는 것이 직관적입니다.

3. 로지스틱 회귀 모델의 필요성

일반적인 선형 회귀 모델은 종속 변수(Y)가 연속형일 때 유용합니다.

하지만 현실에서는 0과 1로 구분되는 이진 변수(binary variable)가 더 자주 등장합니다.

예를 들어:

A가 질병이 발생할 여부(확률)
B가 상품을 구매할 여부(확률)
C가 시험을 통과할 여부(확률)

이처럼 결과 값이 두 개의 범주(0 또는 1)로 나뉠 때, 선형 회귀 모델을 적용하면 예측값이 0보다 작거나 1보다 커지는 문제가 발생합니다.

따라서 이를 해결하기 위해 시그모이드 함수(Sigmoid Function)를 이용하여 예측값을 0과 1 사이로 변환하는 로지스틱 회귀 모델을 사용합니다.

💡 시그모이드 함수(Sigmoid Function) 란?

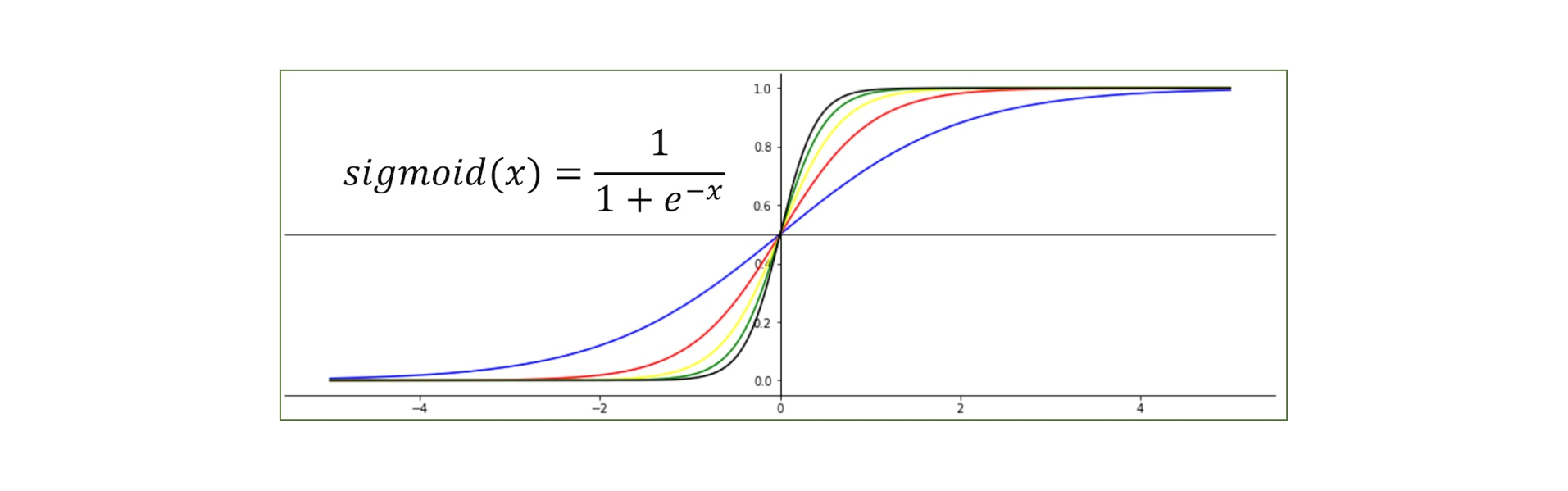
시그모이드 함수는 S자 형태의 곡선을 가지며, 실수 값을 0과 1 사이로 변환하는 비선형 함수입니다.

주어진 입력 x에 대해 다음과 같이 정의됩니다.

sigmoid(x)=11+e−xsigmoid(x) = \frac{1}{1 + e^{-x}}sigmoid(x)=1+e−x1

4. 로지스틱 회귀 모델의 정의

로지스틱 회귀는 시그모이드 함수를 이용해 특정 입력 (XXX)에 대한 확률을 계산하는 모델입니다.

단순히 하나의 (xxx) 값이 아니라, 여러 개의 독립 변수( featuresfeaturesfeatures )들을 고려합니다.

일반적으로 로지스틱 회귀 모델은 선형 회귀 식을 시그모이드 함수에 적용하여 확률을 계산하는 방식으로 정의됩니다.

π(X)=11+e−(β0+β1X1+β2X2+⋯+βnXn)\pi(X) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_n X_n)}}π(X)=1+e−(β0+β1X1+β2X2+⋯+βnXn)1

여기서:

β0\beta_0β0 (절편, bias term)
β1,β2,…,βn\beta_1, \beta_2, …, \beta_nβ1,β2,…,βn (각 변수 X1,X2,…,XnX_1, X_2, …, X_nX1,X2,…,Xn 에 대한 회귀 계수)
X1,X2,…,XnX_1, X_2, …, X_nX1,X2,…,Xn (입력 변수들)

즉, 로지스틱 회귀는 단순히 시그모이드 함수에 선형 결합된 독립 변수들을 대입한 것이라고 볼 수 있습니다.

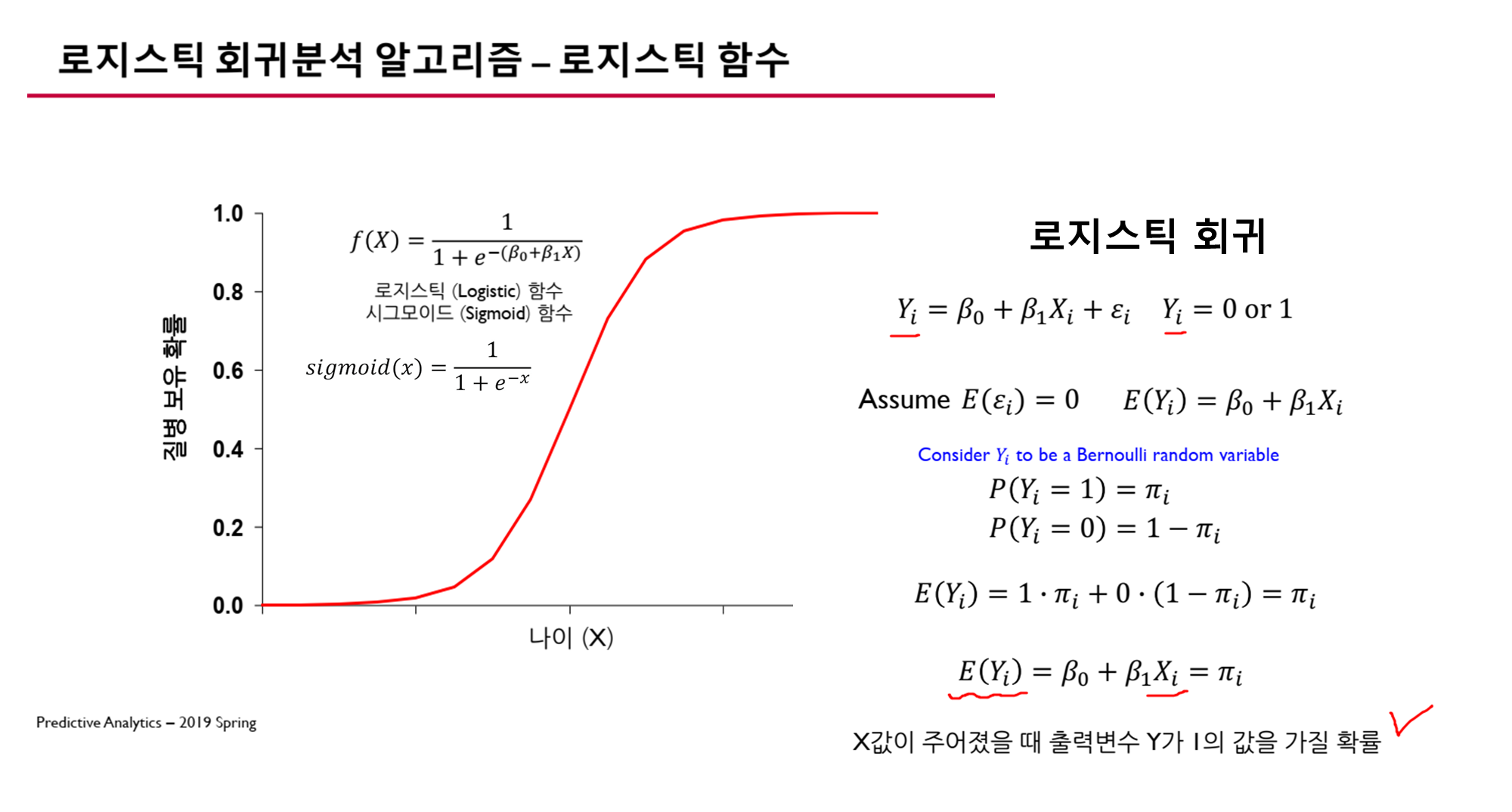
💡 설명의 편의를 위해 하나의 입력변수 X 만 가지고 있는 로지스틱 회귀 모델을 예로 들어 설명하겠습니다.

이는 아래와 같은 수식으로 표현됩니다.

π(X)=11+e−(β0+β1X)\pi(X) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 X)}}π(X)=1+e−(β0+β1X)1

여기서 (π(X)\pi(X)π(X))는 특정 변수가 주어졌을 때 결과가 1이 될 확률을 의미합니다.

📌 Odds(승산):

특정 사건이 발생할 확률과 발생하지 않을 확률의 비율

Odds=π(X)1−π(X)Odds = \frac{\pi(X)}{1 - \pi(X)}Odds=1−π(X)π(X)
- Odds값을 도출하면, 아래와 같은 값이 나옵니다.
Odds=eβ0+β1XOdds = e^{\beta_0 + \beta_1 X}Odds=eβ0+β1X

📌 Logit 변환(Logit Transformation):

Odds에 로그를 취하면 선형 관계로 변환됨

log(Odds)=log(π(X)1−π(X))=log⁡(eβ0+β1X)log(Odds) = log \left( \frac{\pi(X)}{1 - \pi(X)} \right) = \log \left( e^{\beta_0 + \beta_1 X} \right)log(Odds)=log(1−π(X)π(X))=log(eβ0+β1X)
- 로그의 성질을 이용하면,
log⁡(Odds)=β0+β1X\log(Odds) = \beta_0 + \beta_1 Xlog(Odds)=β0+β1X

이를 통해 로지스틱 회귀 모델은 기존 선형 회귀와 비슷한 구조를 가지면서도, 결과값을 확률로 해석할 수 있습니다.

즉, 로지스틱 회귀 모델은 결국 log(Odds)를 선형식으로 표현한 모델입니다.
- 따라서, 우리가 추정하는 회귀 계수(β0,β1\beta_0, \beta_1β0,β1)는 log(Odds)와의 관계를 나타내며, 이를 통해 특정 변수의 변화가 오즈에 미치는 영향을 분석할 수 있습니다. ( log⁡(Odds)=β0+β1X\log(Odds) = \beta_0 + \beta_1 Xlog(Odds)=β0+β1X )

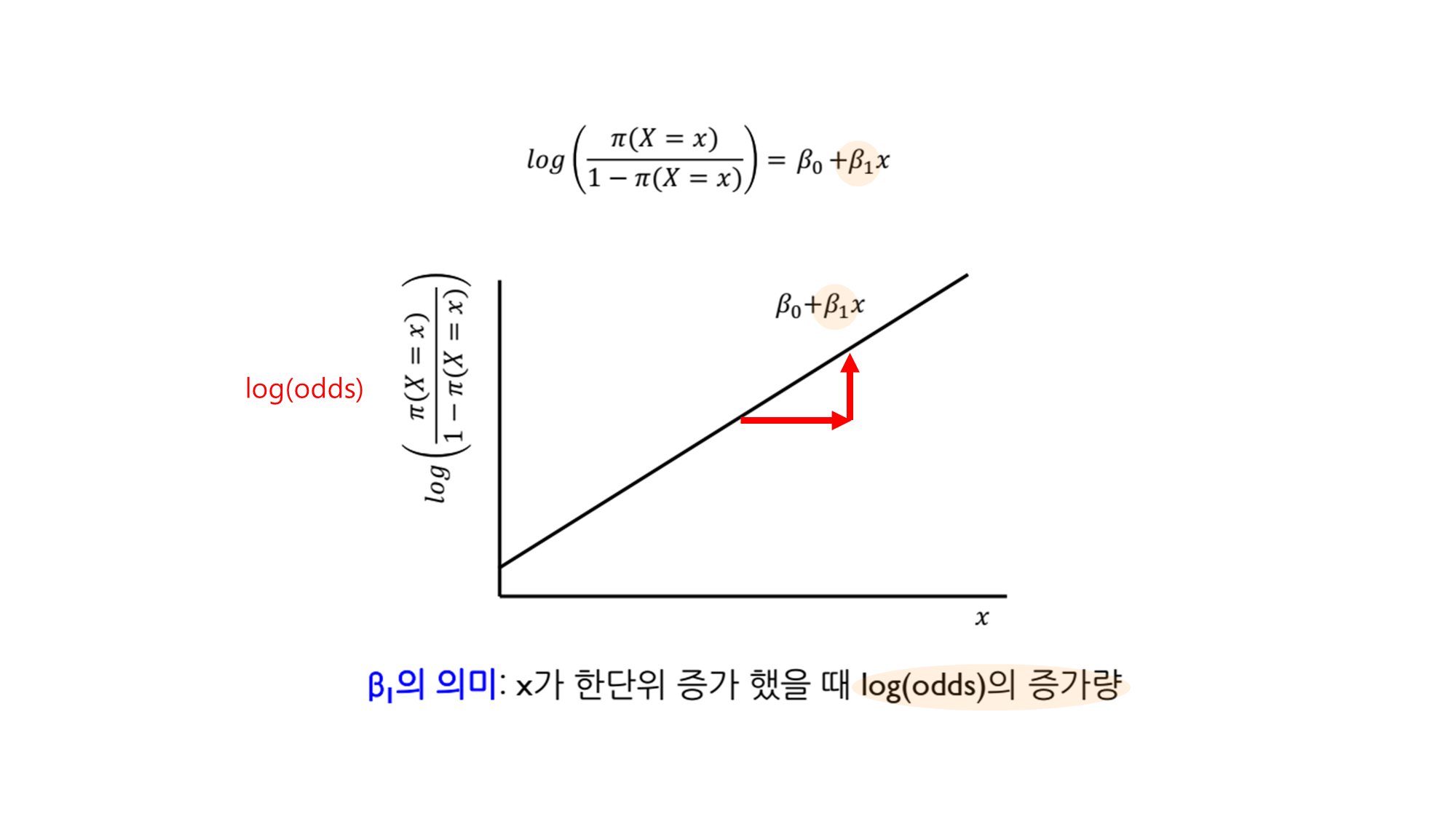
❓ 어? 그렇다면 X의 계수인 β1\beta_1β1에 뭔가 숨겨진 의미가 있을 거 같은데?

β1\beta_1β1의 의미: x가 한단위 증가했을 때 log(odds)의 증가량

이를 지수 함수 형태로 변환하면, X가 한 단위 증가할 때 오즈(odds)가 얼마나 변화하는지를 알 수 있습니다.

eβ1=odds when X+1odds when Xe^{\beta_1} = \frac{\text{odds when } X+1}{\text{odds when } X}eβ1=odds when Xodds when X+1

즉, β1\beta_1β1 값이 0.50.50.5라면 X가 111 증가할 때 odds가 e0.5≈1.65e^{0.5} \approx 1.65e0.5≈1.65배 증가한다는 의미입니다.

만약 회귀계수가 여러개라면, 각각의 회귀 계수(β1,β2,…,βn\beta_1, \beta_2, …, \beta_nβ1,β2,…,βn)는 각 독립 변수들이 종속 변수에 미치는 개별적인 영향을 나타냅니다.

log⁡(Odds)=β0+β1X1+β2X2+⋯+βnXn\log(Odds) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_n X_nlog(Odds)=β0+β1X1+β2X2+⋯+βnXn

여기서 βi\beta_iβi는 해당 변수 XiX_iXi가 한 단위 증가할 때 log(odds)가 변하는 양을 의미합니다.

만약 β2=0.7\beta_2 = 0.7β2=0.7이라면, X2X_2X2가 1 증가할 때 odds는 e0.7≈2.01e^{0.7} \approx 2.01e0.7≈2.01배 증가한다는 뜻입니다.

반면 β3=−0.5\beta_3 = -0.5β3=−0.5라면, X3X_3X3가 1 증가할 때 odds는 e−0.5≈0.61e^{-0.5} \approx 0.61e−0.5≈0.61배 감소한다는 뜻입니다.

이를 통해 각 독립 변수들이 결과 변수에 미치는 영향을 개별적으로 해석할 수 있습니다.

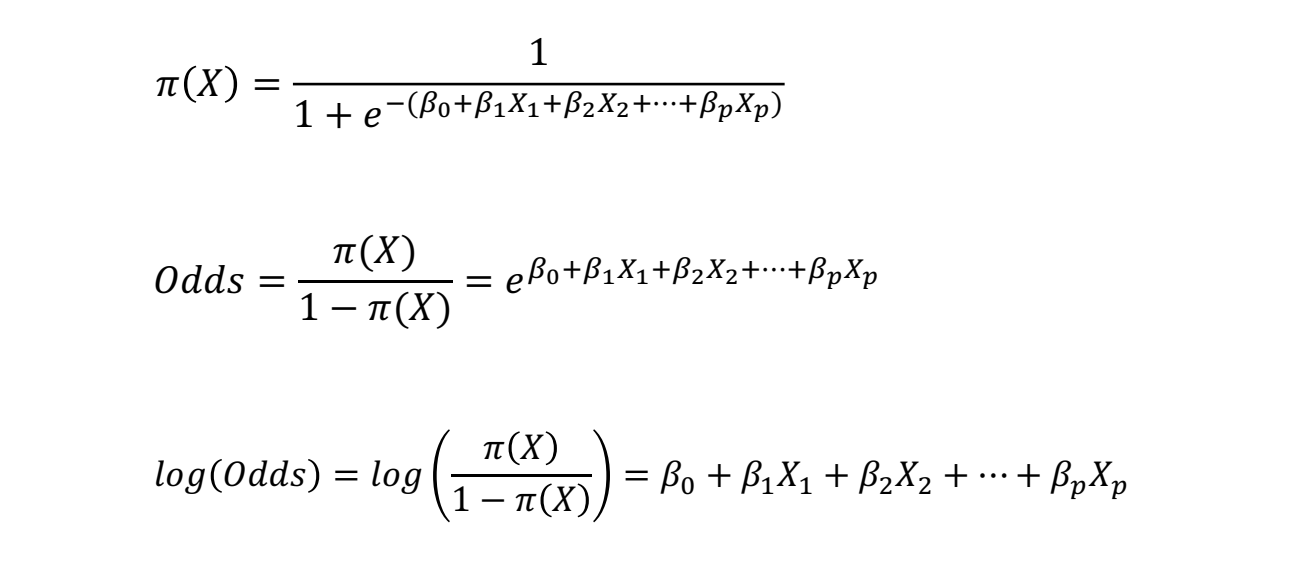
Equation. 로지스틱 함수, 오즈(승산), 로짓변환(Logistic 회귀모델)

항목	시그모이드 함수	로지스틱 함수	로지스틱 회귀
정의	활성화 함수로 사용되는 함수	S자 모양의 수학적 함수	이진 분류를 위한 통계 모델
수식	11+e−x\frac{1}{1 + e^{-x}}1+e−x1	11+e−(β0+βx)\frac{1}{1 + e^{-(\beta_0 + \beta x)}}1+e−(β0+βx)1	log⁡(Odds)=β0+β1X\log(Odds) = \beta_0 + \beta_1 Xlog(Odds)=β0+β1X
주요 사용처	신경망의 비선형 변환	확률 모델링	분류 문제 (예: 스팸/비스팸)
맥락	딥러닝 및 활성화 함수	수학적 개념	통계/머신러닝 모델
관계	로지스틱 함수와 수식 동일	로지스틱 회귀의 기반이 됨	시그모이드 함수를 활용

Table. 시그모이드 함수 / 로지스틱 함수 / 로지스틱 회귀

5. 로지스틱 회귀 모델의 파라미터 추정 방법

5.1. 로지스틱 회귀의 목적

로지스틱 회귀(Logistic Regression)는 이진 분류(Binary Classification) 문제를 해결하기 위한 선형 모델입니다.
- 출력 값 yyy는 0 또는 1이며, 입력 데이터 xxx에 대한 조건부 확률은 시그모이드(Sigmoid) 함수로 표현됩니다.

π(xi)=P(yi=1∣xi)=eβ0+β1Xi1+⋯+βpXip1+eβ0+β1Xi1+⋯+βpXip\pi(x_i) = P(y_i = 1

x_i) = \frac{e^{\beta_0 + \beta_1 X_{i1} + \dots + \beta_p X_{ip}}}{1 + e^{\beta_0 + \beta_1 X_{i1} + \dots + \beta_p X_{ip}}}π(xi)=P(yi=1∣xi)=1+eβ0+β1Xi1+⋯+βpXipeβ0+β1Xi1+⋯+βpXip

즉, 모델은 입력 xix_ixi가 주어졌을 때 yi=1y_i = 1yi=1일 확률을 예측합니다.

5.2. 최대 우도 추정(MLE, Maximum Likelihood Estimation)

MLE의 목표는 주어진 데이터에 대해 가장 가능성이 높은 모델 파라미터 β\betaβ를 찾는 것입니다.

각 데이터 포인트 (xi,yi)(x_i, y_i)(xi,yi)에 대한 확률은 다음과 같이 정의됩니다.

yi=1y_i = 1yi=1일 확률: P(yi=1)=π(xi)P(y_i = 1) = \pi(x_i)P(yi=1)=π(xi)
yi=0y_i = 0yi=0일 확률: P(yi=0)=1−π(xi)P(y_i = 0) = 1 - \pi(x_i)P(yi=0)=1−π(xi)

전체 데이터 샘플 nnn개에 대한 우도 함수(Likelihood Function) L(β)L(\beta)L(β)는 개별 확률의 곱으로 표현됩니다.

L(β)=∏i=1nπ(xi)yi(1−π(xi))1−yiL(\beta) = \prod_{i=1}^{n} \pi(x_i)^{y_i} (1 - \pi(x_i))^{1 - y_i}L(β)=i=1∏nπ(xi)yi(1−π(xi))1−yi

이 우도 함수 L(β)L(\beta)L(β)를 최대로 만드는 β\betaβ를 찾는 것이 MLE의 목표입니다.

5.3. 로그 가능도(Log-Likelihood) 함수

우도 함수는 곱 형태이므로 최적화를 쉽게 하기 위해 로그를 취합니다.

ln⁡L(β)=∑i=1n(yiln⁡π(xi)+(1−yi)ln⁡(1−π(xi)))\ln L(\beta) = \sum_{i=1}^{n} \left( y_i \ln \pi(x_i) + (1 - y_i) \ln(1 - \pi(x_i)) \right)lnL(β)=i=1∑n(yilnπ(xi)+(1−yi)ln(1−π(xi)))

이 로그 가능도 함수(ln⁡L\ln LlnL)를 최대화하면 최적의 β\betaβ를 찾을 수 있습니다.

❓ (참고) 로그 가능도(Log-Likelihood) 함수 자세하게 살펴보기

로그 가능도(Log-Likelihood) 함수는 우도 함수에 로그를 취한 형태입니다.

ln⁡L=∑i(yiln⁡π(xi)+(1−yi)ln⁡(1−π(xi)))\ln L = \sum_i \left( y_i \ln \pi(x_i) + (1 - y_i) \ln(1 - \pi(x_i)) \right)lnL=i∑(yilnπ(xi)+(1−yi)ln(1−π(xi)))

이제 시그모이드 함수 π(xi)\pi(x_i)π(xi)를 대입합니다.

π(xi)=eβ0+β1X1+⋯+βpXp1+eβ0+β1X1+⋯+βpXp\pi(x_i) = \frac{e^{\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p}}{1 + e^{\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p}}π(xi)=1+eβ0+β1X1+⋯+βpXpeβ0+β1X1+⋯+βpXp

이를 ln⁡π(xi)\ln \pi(x_i)lnπ(xi)와 ln⁡(1−π(xi))\ln(1 - \pi(x_i))ln(1−π(xi))에 적용하면:

ln⁡π(xi)=ln⁡(eβ0+β1X1+⋯+βpXp1+eβ0+β1X1+⋯+βpXp)\ln \pi(x_i) = \ln \left( \frac{e^{\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p}}{1 + e^{\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p}} \right)lnπ(xi)=ln(1+eβ0+β1X1+⋯+βpXpeβ0+β1X1+⋯+βpXp)

=(β0+β1X1+⋯+βpXp)−ln⁡(1+eβ0+β1X1+⋯+βpXp)= (\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p) - \ln(1 + e^{\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p})=(β0+β1X1+⋯+βpXp)−ln(1+eβ0+β1X1+⋯+βpXp)

ln⁡(1−π(xi))=ln⁡(11+eβ0+β1X1+⋯+βpXp)\ln(1 - \pi(x_i)) = \ln \left( \frac{1}{1 + e^{\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p}} \right)ln(1−π(xi))=ln(1+eβ0+β1X1+⋯+βpXp1)

=−ln⁡(1+eβ0+β1X1+⋯+βpXp)= -\ln(1 + e^{\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p})=−ln(1+eβ0+β1X1+⋯+βpXp)

이제 이를 로그 가능도 함수에 대입하면:

ln⁡L=∑iyi((β0+β1X1+⋯+βpXp)−ln⁡(1+eβ0+β1X1+⋯+βpXp))\ln L = \sum_i y_i \left( (\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p) - \ln(1 + e^{\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p}) \right)lnL=i∑yi((β0+β1X1+⋯+βpXp)−ln(1+eβ0+β1X1+⋯+βpXp))

+∑i(1−yi)(−ln⁡(1+eβ0+β1X1+⋯+βpXp))+ \sum_i (1 - y_i) \left( -\ln(1 + e^{\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p}) \right)+i∑(1−yi)(−ln(1+eβ0+β1X1+⋯+βpXp))

이를 전개하면:

∑iyi(β0+β1X1+⋯+βpXp)−∑iyiln⁡(1+eβ0+β1X1+⋯+βpXp)\sum_i y_i (\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p) - \sum_i y_i \ln(1 + e^{\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p})i∑yi(β0+β1X1+⋯+βpXp)−i∑yiln(1+eβ0+β1X1+⋯+βpXp)

−∑i(1−yi)ln⁡(1+eβ0+β1X1+⋯+βpXp)- \sum_i (1 - y_i) \ln(1 + e^{\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p})−i∑(1−yi)ln(1+eβ0+β1X1+⋯+βpXp)

이제 두 번째, 세 번째 항을 합치면:

∑iyi(β0+β1X1+⋯+βpXp)−∑iln⁡(1+eβ0+β1X1+⋯+βpXp)\sum_i y_i (\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p) - \sum_i \ln(1 + e^{\beta_0 + \beta_1 X_1 + \dots + \beta_p X_p})i∑yi(β0+β1X1+⋯+βpXp)−i∑ln(1+eβ0+β1X1+⋯+βpXp)

위 로그-우도함수(log likelihood function)가 최대가 되는 파라미터 β를 찾는 것이 목적
로그-우도함수(log likelihood function)는 파라미터β에 대해 비선형이므로 선형회귀
모델과 같이 명시적인 해가 존재하지 않음 (이를 “No closed-form solution exists”이라고 함)

따라서, 우리는 아래 5.4. 로지스틱 회귀의 손실 함수 (Cost Function)와 같은 최적화 접근으로 이를 도출하고자 함.

5.4. 로지스틱 회귀의 손실 함수 (Cost Function)

머신러닝에서는 최적화 문제를 최소화(Minimization) 형태로 바꾸는 것이 일반적입니다.
- 이를 위해 로그 가능도 함수의 부호를 반전시켜서 Negative Log-Likelihood (NLL)을 정의합니다.
- 최적화 과정에서 우리는 우도를 최대화하는 대신 손실을 최소화하는 문제로 변환합니다.

J(β)=−ln⁡L(β)J(\beta) = -\ln L(\beta)J(β)=−lnL(β)

📖 (정리) 즉, 최대 우도 추정(MLE)에서는 ln(𝐿)ln(𝐿)ln(L)을 최대로 만드는 것이 목표지만, 머신러닝에서는 일반적으로 손실(loss) 함수를 최소화하는 방식으로 최적화합니다.

이를 위해 Negative Log-Likelihood (NLL), 즉 음의 로그 가능도를 사용합니다.

max⁡βln⁡L(β)⇒min⁡β−ln⁡L(β)\max_{\beta} \ln L(\beta) \quad \Rightarrow \quad \min_{\beta} -\ln L(\beta)βmaxlnL(β)⇒βmin−lnL(β)

J(β)=−∑i=1n(yiln⁡π(xi)+(1−yi)ln⁡(1−π(xi)))J(\beta) = - \sum_{i=1}^{n} \left( y_i \ln \pi(x_i) + (1 - y_i) \ln(1 - \pi(x_i)) \right)J(β)=−i=1∑n(yilnπ(xi)+(1−yi)ln(1−π(xi)))

이 식은 Binary Cross-Entropy (BCE) 손실 함수와 동일합니다.

J(β)=−1n∑i=1n(yiln⁡π(xi)+(1−yi)ln⁡(1−π(xi)))J(\beta) = -\frac{1}{n} \sum_{i=1}^{n} \left( y_i \ln \pi(x_i) + (1 - y_i) \ln(1 - \pi(x_i)) \right)J(β)=−n1i=1∑n(yilnπ(xi)+(1−yi)ln(1−π(xi)))

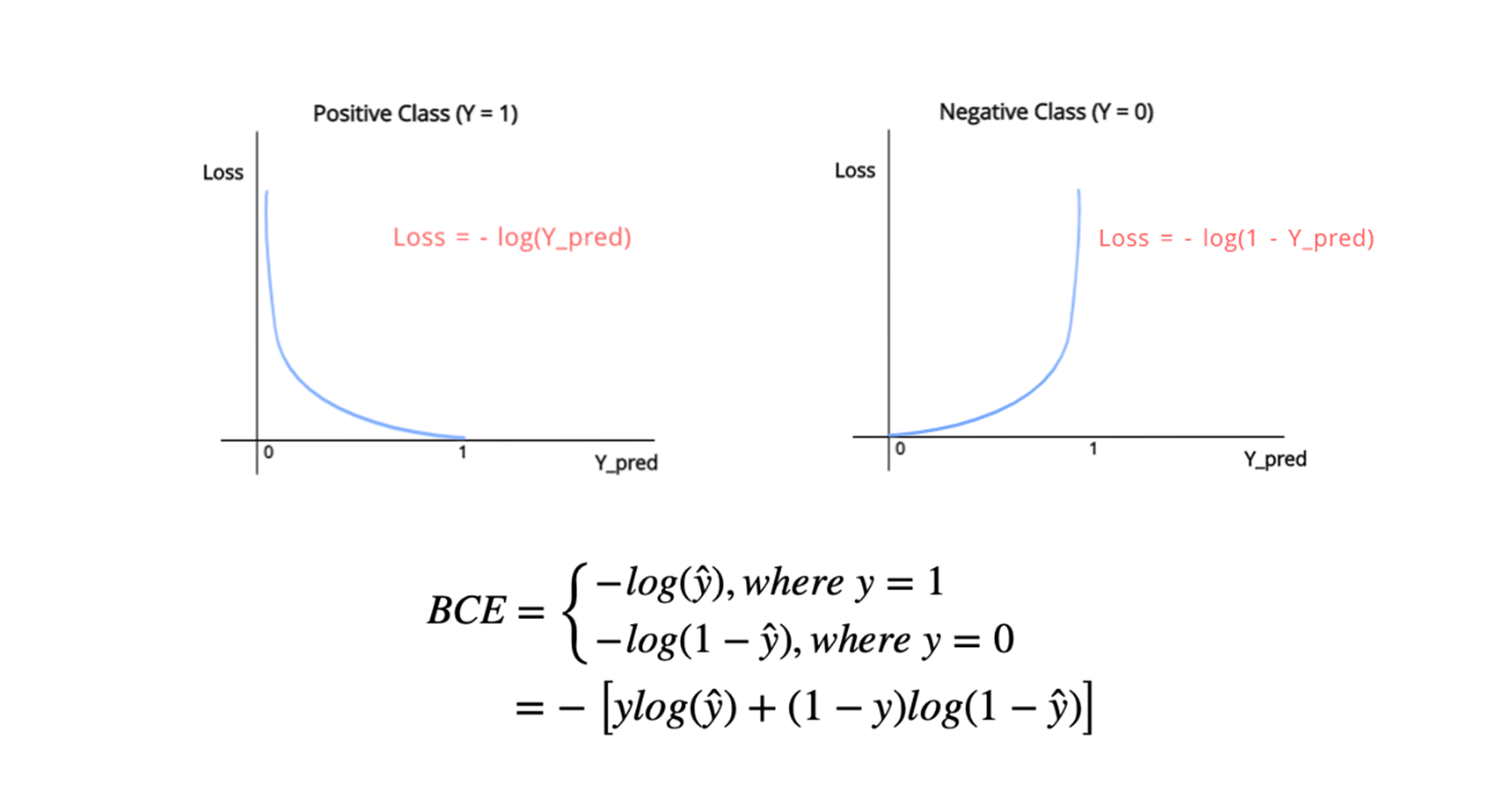
참고 : Binary Cross-Entropy (BCE) 손실 함수

즉, 로지스틱 회귀의 MLE 문제는 결국 Cross-Entropy 손실을 최소화하는 문제와 같아집니다.

5.5. argmax 관점에서 해석

MLE의 목표는 로그 가능도 ln⁡L(β)\ln L(\beta)lnL(β)를 최대화하는 β\betaβ를 찾는 것입니다.

β^=arg⁡max⁡βln⁡L(β)\hat{\beta} = \arg\max_{\beta} \ln L(\beta)β^=argβmaxlnL(β)

하지만 머신러닝에서는 손실 함수(Cost Function)를 최소화하는 문제로 변환합니다.

β^=arg⁡min⁡βJ(β)=arg⁡min⁡β−ln⁡L(β)\hat{\beta} = \arg\min_{\beta} J(\beta) = \arg\min_{\beta} -\ln L(\beta)β^=argβminJ(β)=argβmin−lnL(β)

즉, 로그 가능도를 최대화하는 것과 Negative Log-Likelihood를 최소화하는 것은 동등한 문제입니다.

5.6. 최종 정리

개념	목적	표현식
최대 우도 추정 (MLE)	우도를 최대화하는 β\betaβ 찾기	L(β)=∏i=1nπ(xi)yi(1−π(xi))1−yiL(\beta) = \prod_{i=1}^{n} \pi(x_i)^{y_i} (1 - \pi(x_i))^{1 - y_i}L(β)=∏i=1nπ(xi)yi(1−π(xi))1−yi
로그 가능도 (Log-Likelihood)	우도의 로그를 취해 최대화	ln⁡L=∑i=1n(yiln⁡π(xi)+(1−yi)ln⁡(1−π(xi)))\ln L = \sum_{i=1}^{n} \left( y_i \ln \pi(x_i) + (1 - y_i) \ln(1 - \pi(x_i)) \right)lnL=∑i=1n(yilnπ(xi)+(1−yi)ln(1−π(xi)))
Negative Log-Likelihood (NLL)	로그 가능도의 부호를 바꿔 최소화	J(β)=−ln⁡L(β)=−∑i=1n(yiln⁡π(xi)+(1−yi)ln⁡(1−π(xi)))J(\beta) = -\ln L(\beta) = -\sum_{i=1}^{n} \left( y_i \ln \pi(x_i) + (1 - y_i) \ln(1 - \pi(x_i)) \right)J(β)=−lnL(β)=−∑i=1n(yilnπ(xi)+(1−yi)ln(1−π(xi)))
Binary Cross-Entropy (BCE) 손실 함수	로지스틱 회귀에서 최적화하는 표준 손실 함수	J(β)=−1n∑i=1n(yiln⁡π(xi)+(1−yi)ln⁡(1−π(xi)))J(\beta) = -\frac{1}{n} \sum_{i=1}^{n} \left( y_i \ln \pi(x_i) + (1 - y_i) \ln(1 - \pi(x_i)) \right)J(β)=−n1∑i=1n(yilnπ(xi)+(1−yi)ln(1−π(xi)))

즉, MLE에서 로그 가능도를 최대화하는 문제는 결국 Cross-Entropy 손실을 최소화하는 문제와 같아집니다.

이는 우리가 흔히 로지스틱 회귀의 손실 함수(Binary Cross-Entropy, BCE)를 사용하는 이유입니다.

6. 로지스틱 회귀모델 결과 해석

로지스틱 회귀모델을 생성한 후 나오는 결과 테이블의 결과를 해석하는 방법을 설명합니다.

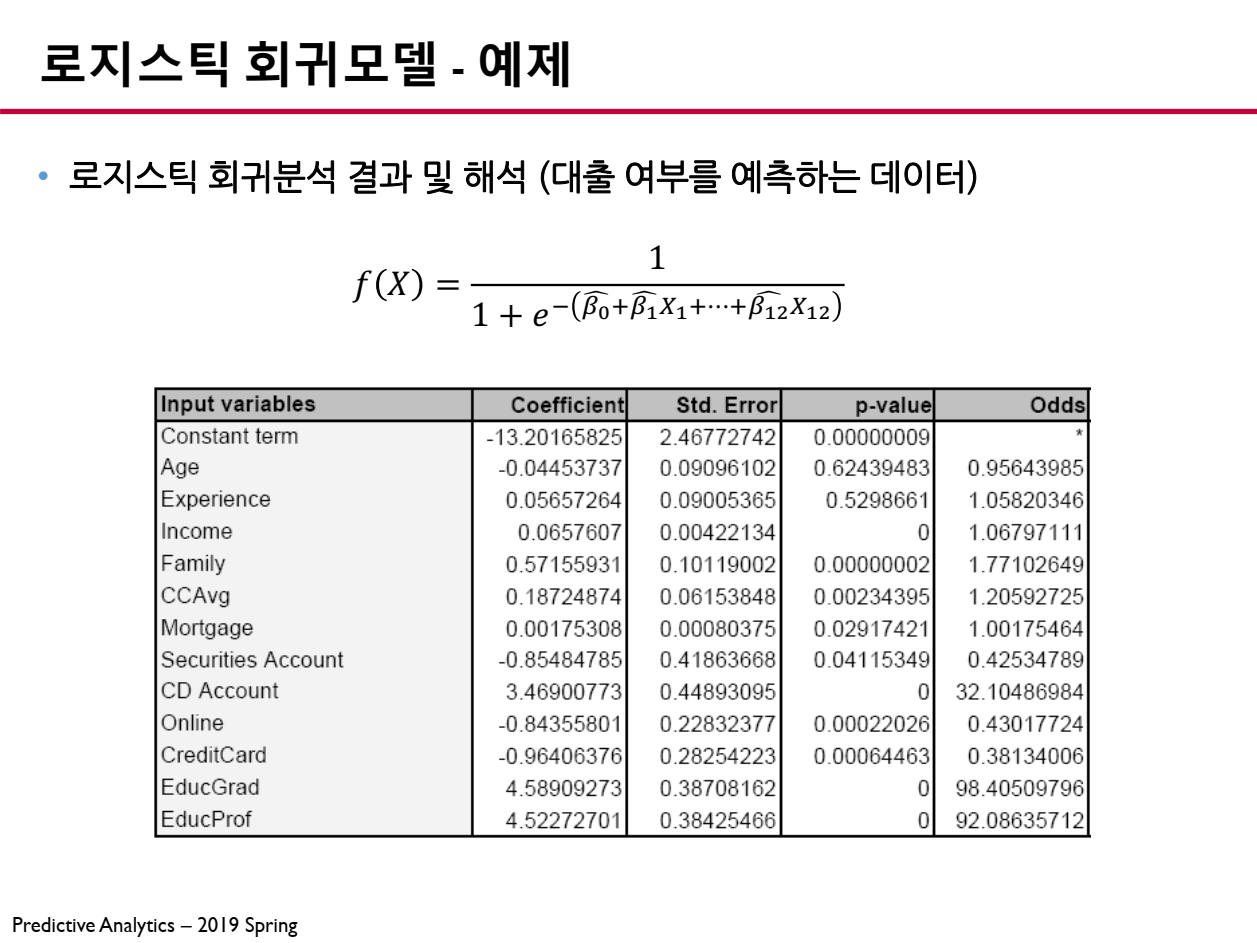
6.1 추정된 파라미터 (Coefficient)

로지스틱 회귀모델에서 파라미터 (Coefficient, β\betaβ)는 테이블의 결과에서 로그 오즈(Log-Odds) 변화량을 나타냅니다.

log⁡(π(x)1−π(x))=β0+β1X1+⋯+βpXp\log \left( \frac{\pi(x)}{1 - \pi(x)} \right) = \beta_0 + \beta_1 X_1 + \dots + \beta_p X_plog(1−π(x)π(x))=β0+β1X1+⋯+βpXp

β>0\beta > 0β>0 : 해당 변수가 증가할 때 성공 확률이 증가
β<0\beta < 0β<0 : 해당 변수가 증가할 때 성공 확률이 감소

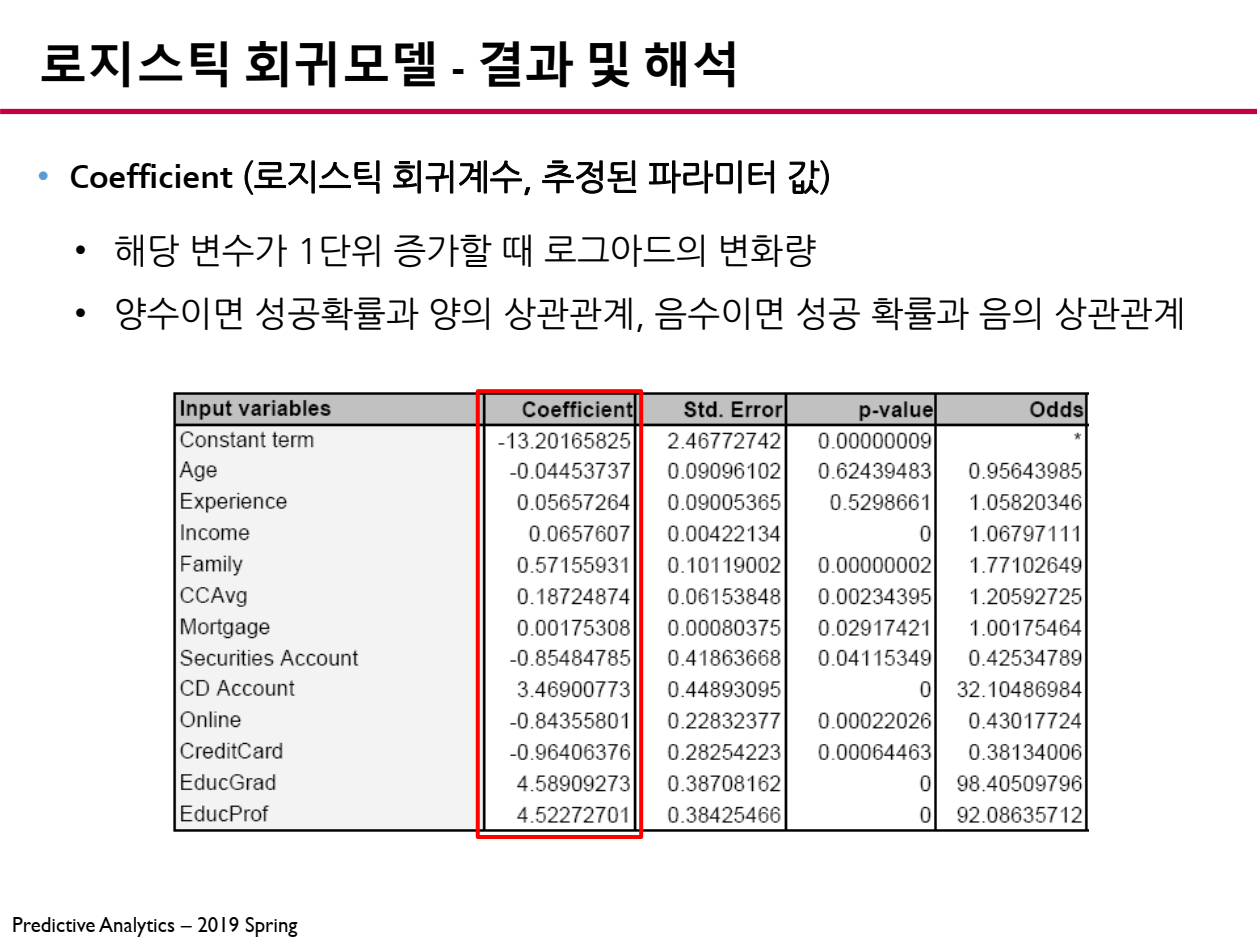
따라서, 회귀계수가 증가하면 성공 확률이 증가하고, 회귀계수가 음수면 성공 확률이 감소하는 것을 의미합니다.

6.2 파라미터 표준편차 (Standard Error)

추정된 파라미터의 표준편차 (Standard Error, SE)는 해당 파라미터가 얼마나 신뢰할 수 있는지를 나타냅니다.

Std. Error가 작을수록 : 파라미터 결과의 신뢰성이 높음
Std. Error가 크면 : 파라미터 결과의 신뢰성이 낮음

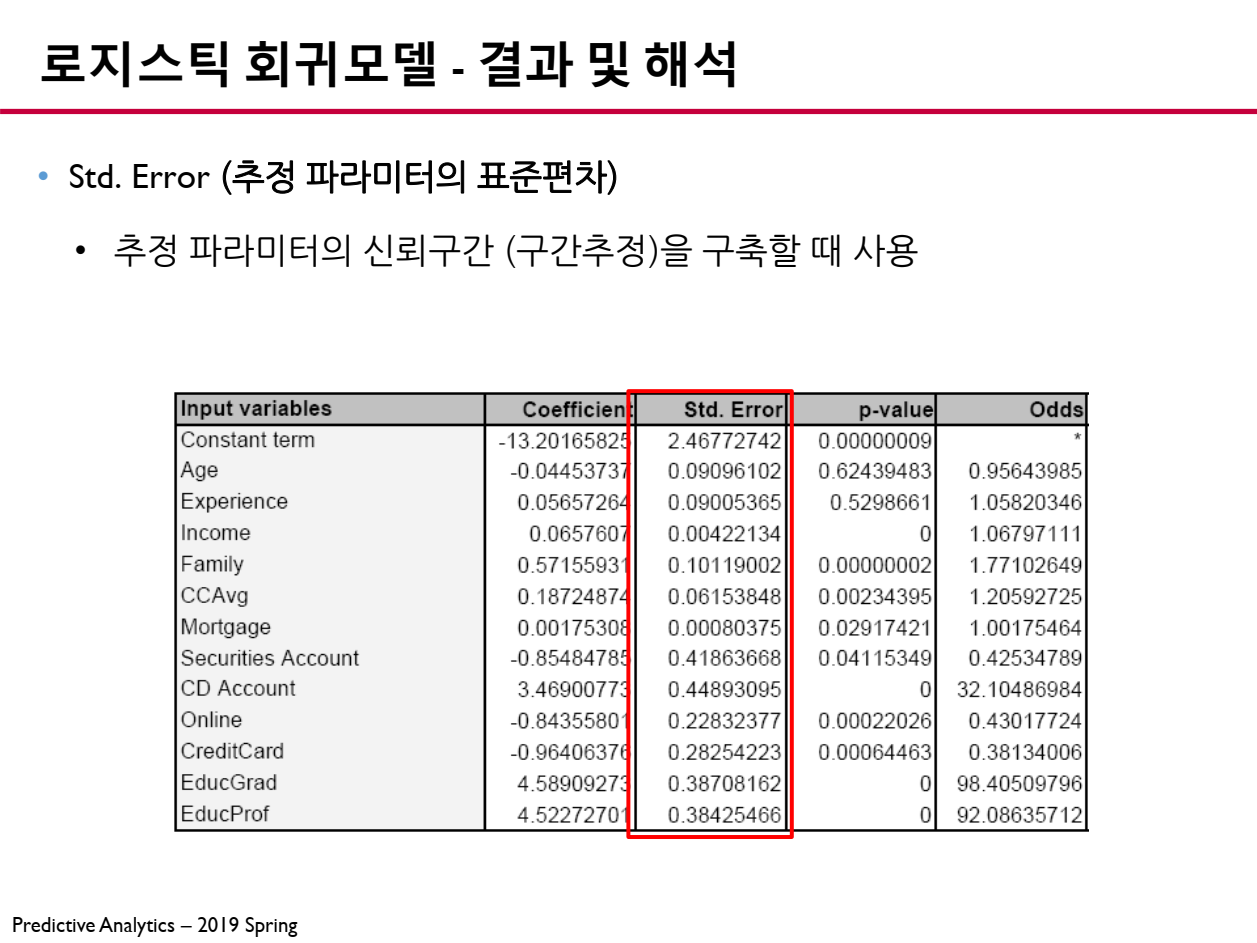
이 값은 신뢰구간 (Confidence Interval, CI) 계산에 사용됩니다.

95% CI=β±1.96×Std. Error95\% \text{ CI} = \beta \pm 1.96 \times \text{Std. Error}95% CI=β±1.96×Std. Error

6.3 p-value (통계적 유의성)

p-value는 해당 파라미터가 종속 변수에 유의미한 영향을 미치는지를 판단하는 값입니다.

p-value < 0.05 : 해당 변수는 종속 변수에 유의미한 영향을 준다.
p-value \geq 0.05 : 해당 변수는 종속 변수에 유의미한 영향을 주지 않는다.

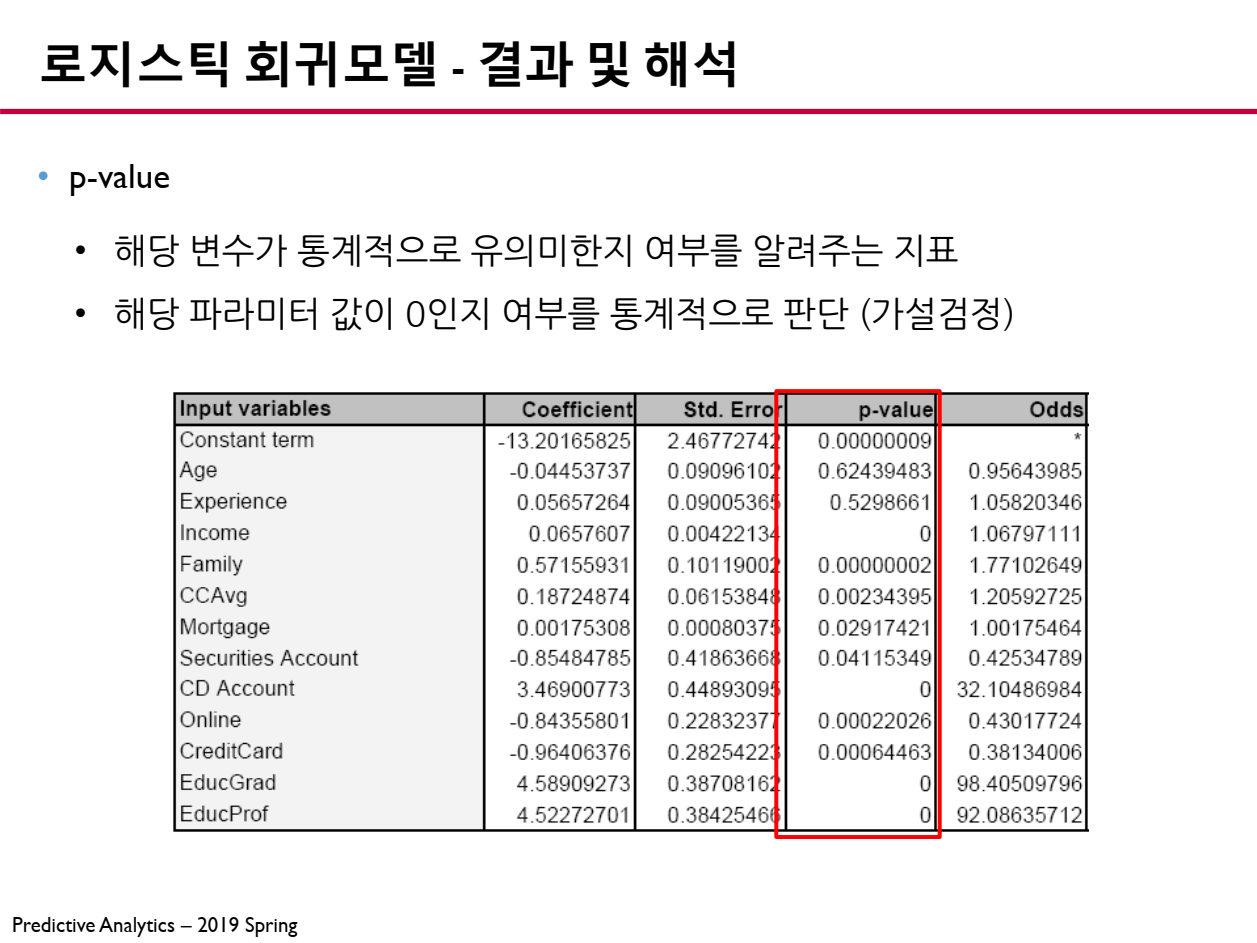
p-value가 0.05보다 작으면 해당 파라미터는 종속 변수에 유의미한 영향을 준다고 판단할 수 있습니다.

6.4 Odds Ratio (승산 비율)

로지스틱 회귀모델에서 Odds Ratio(승산 비율)은 특정 변수가 1 증가할 때 성공(종속 변수 Y=1Y=1Y=1)의 오즈(Odds)가 몇 배 변화하는지를 나타내는 값입니다.

우리가 얻는 회귀계수 β\betaβ는 로그 오즈(Log-Odds)의 변화량을 의미하며, 이를 지수 함수 eβe^{\beta}eβ로 변환하면 Odds Ratio(승산 비율)을 얻을 수 있습니다.

Odds Ratio=eβ\text{Odds Ratio} = e^{\beta}Odds Ratio=eβ

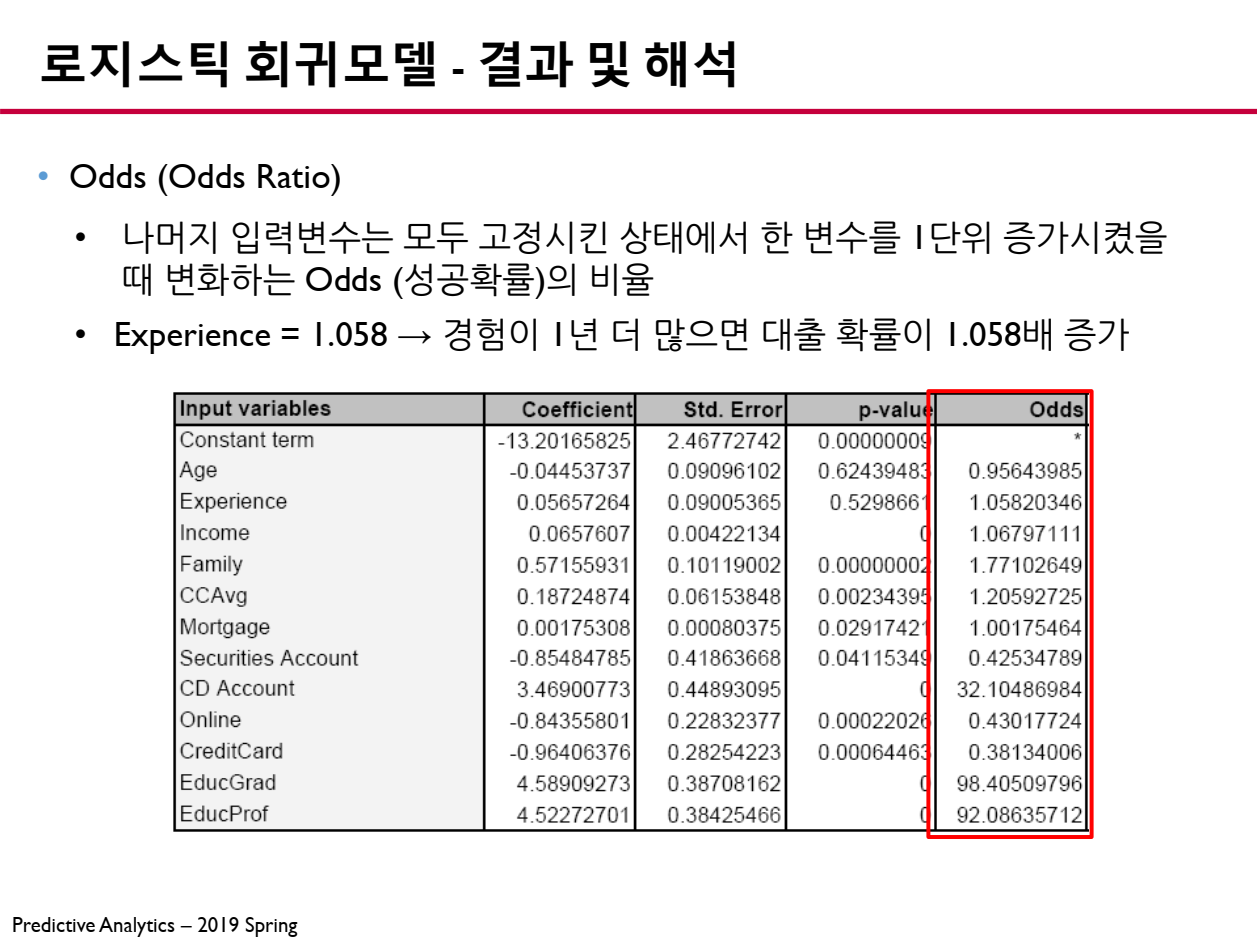
📖 Odds Ratio 해석

Odds Ratio > 1 : 해당 변수가 증가하면 성공 확률이 증가함.

예: Odds Ratio=1.5\text{Odds Ratio} = 1.5Odds Ratio=1.5라면, 해당 변수가 1 증가할 때 성공할 확률이 1.5배 증가함.

Odds Ratio = 1 : 해당 변수가 성공 확률에 영향을 주지 않음.

Odds Ratio < 1 : 해당 변수가 증가하면 성공 확률이 감소함.

예: Odds Ratio=0.5\text{Odds Ratio} = 0.5Odds Ratio=0.5라면, 해당 변수가 1 증가할 때 성공할 확률이 절반(50%)로 감소함.

7. 결론

로지스틱 회귀 모델은 범주형 데이터를 예측하는 데 유용한 도구이며, 오즈 비를 통해 변수 간의 관계를 명확하게 분석할 수 있습니다.

연구자와 실험자들은 이를 활용하여 실험 데이터를 보다 직관적으로 해석하고, 의미 있는 연구 결과를 도출할 수 있습니다.

앞으로 실험 데이터를 분석할 때, 오즈 비를 활용해보시길 추천드립니다!

화이팅입니다 💌