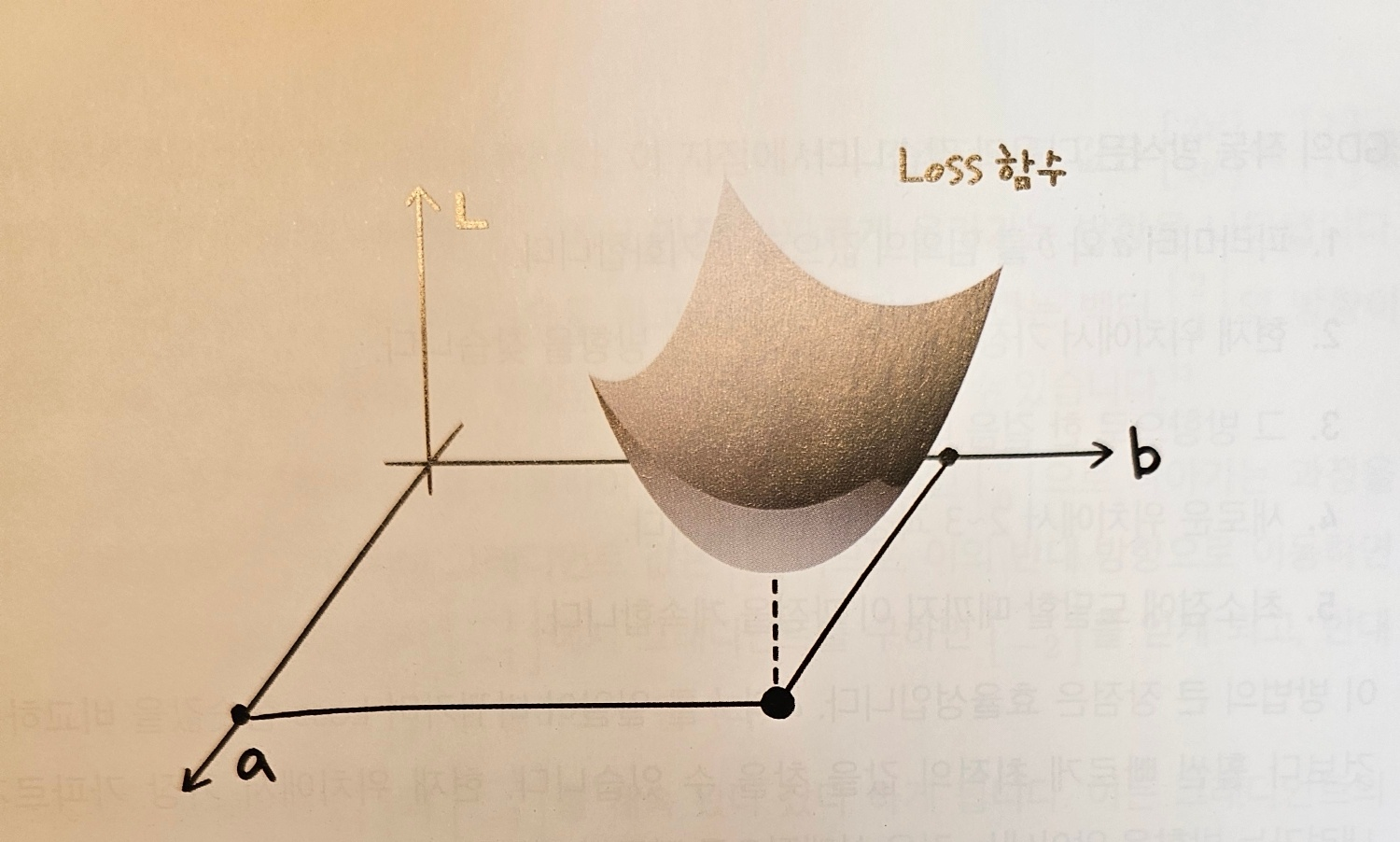
[도서리뷰] 경사 하강법 계보 정리(혁펜하임의 『Easy! 딥러닝』)

안녕하세요! 지난 『Easy! 딥러닝』 도서 소개 게시글(딥러닝 입문자를 위한 책 추천, 혁펜하임 『Easy! 딥러닝』)에 이어서 오늘은 핵심 챕터 분석 및 심층 탐구를 해보겠습니다
📸 (참고) 책 이미지들은 리뷰 목적으로 직접 촬영 후 첨부하였습니다.
이번 게시글에서는 “Chapter 2 – 인공 신경망과 선형 회귀, 그리고 최적화 기법들”을 다룰 예정입니다.
- 이 장에서는 인공 신경망, 선형 회귀, 그리고 최적화 기법 등 딥러닝을 이해하는 데 필수적인 핵심 개념들을 소개합니다.
💬 Table of Contents for Chapter 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
✅ Chapter 2 – 인공 신경망과 선형 회귀, 그리고 최적화 기법들
2.1 인공 신경: Weight와 Bias의 직관적 이해
2.2 인공 신경망과 MLP
2.3 인공 신경망은 함수다!
2.4 선형 회귀, 개념부터 알고리즘까지 step by step
2.5 경사 하강법
2.5.1 경사 하강법의 두 가지 문제
2.6 웨이트 초기화
2.7 확률적 경사 하강법
2.8 Mini-Batch Gradient Descent
2.8.1 Batch Size와 Learning Rate의 조절
2.9 Momentum
2.10 RMSProp
2.11 Adam
2.12 검증 데이터
2.12.1 K-fold 교차 검증
저도 이번에 이 책의 리뷰어로 선정되어 내용을 다시 살펴보면서, 친절한 예시와 쉬운 설명 덕분에 딥러닝 개념을 보다 탄탄하게 정리할 수 있었습니다.
- 전공서의 딱딱한 설명이 부담스러우셨다면, 이 책은 입문자에게도 부담 없이 추천할 만한 책입니다!
기울기와 최적화 기법
1. 그래디언트(Gradient)란?
그래디언트는 다변수 함수에서 함수값이 가장 가파르게 증가하는 방향과 그 크기를 나타내는 벡터입니다.
Ex. 어떤 함수 f(x,y)f(x,y)f(x,y)가 있을 때, 특정 지점에서의 그래디언트는 각 변수에 대한 편미분(partial derivative)으로 구할 수 있습니다.
∇f(x,y)=[∂f∂x,∂f∂y]\nabla f(x, y) = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]∇f(x,y)=[∂x∂f,∂y∂f]
이 그래디언트 벡터는 해당 지점에서 함수가 가장 빠르게 증가하는 방향을 가리킵니다.
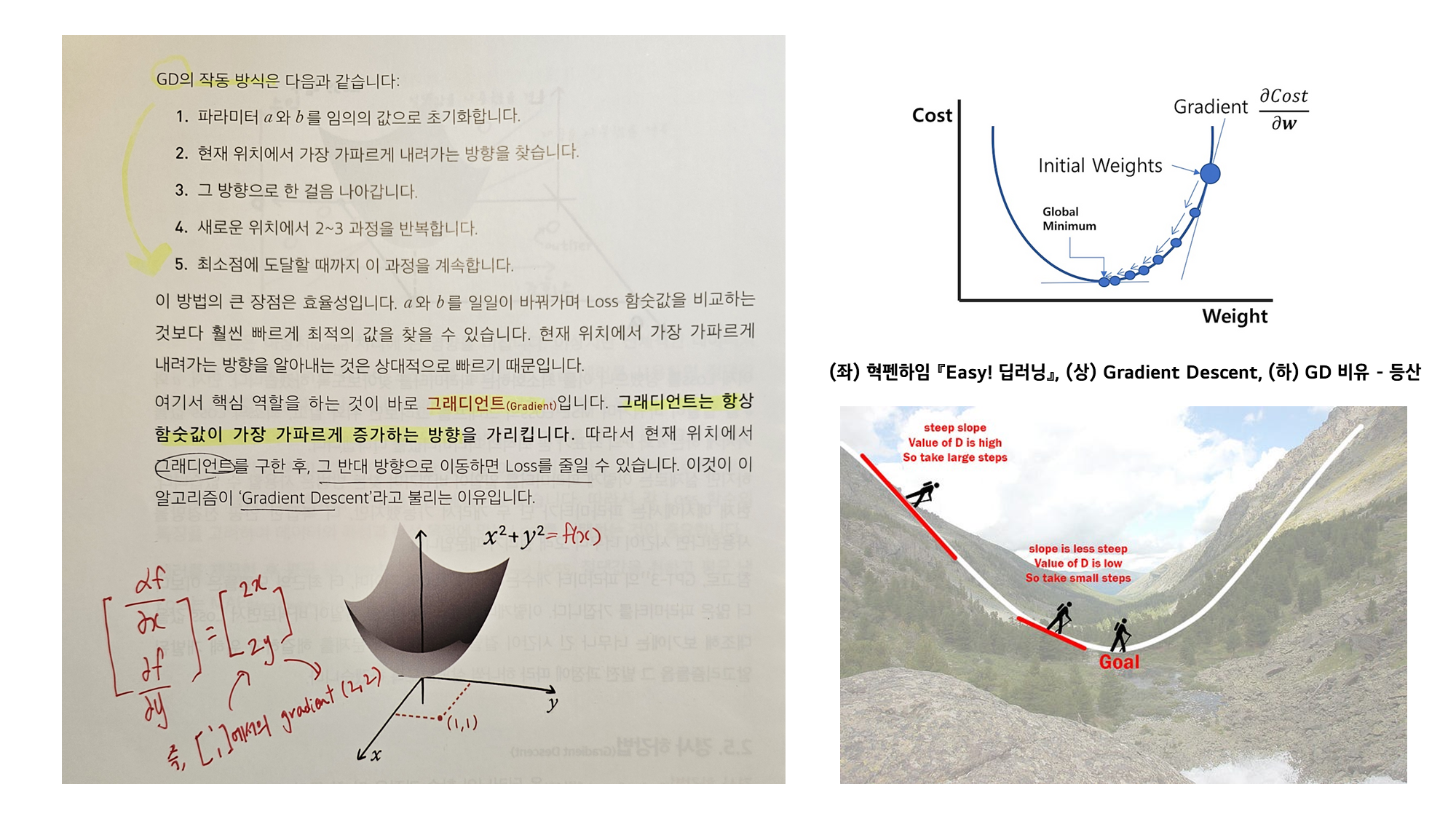
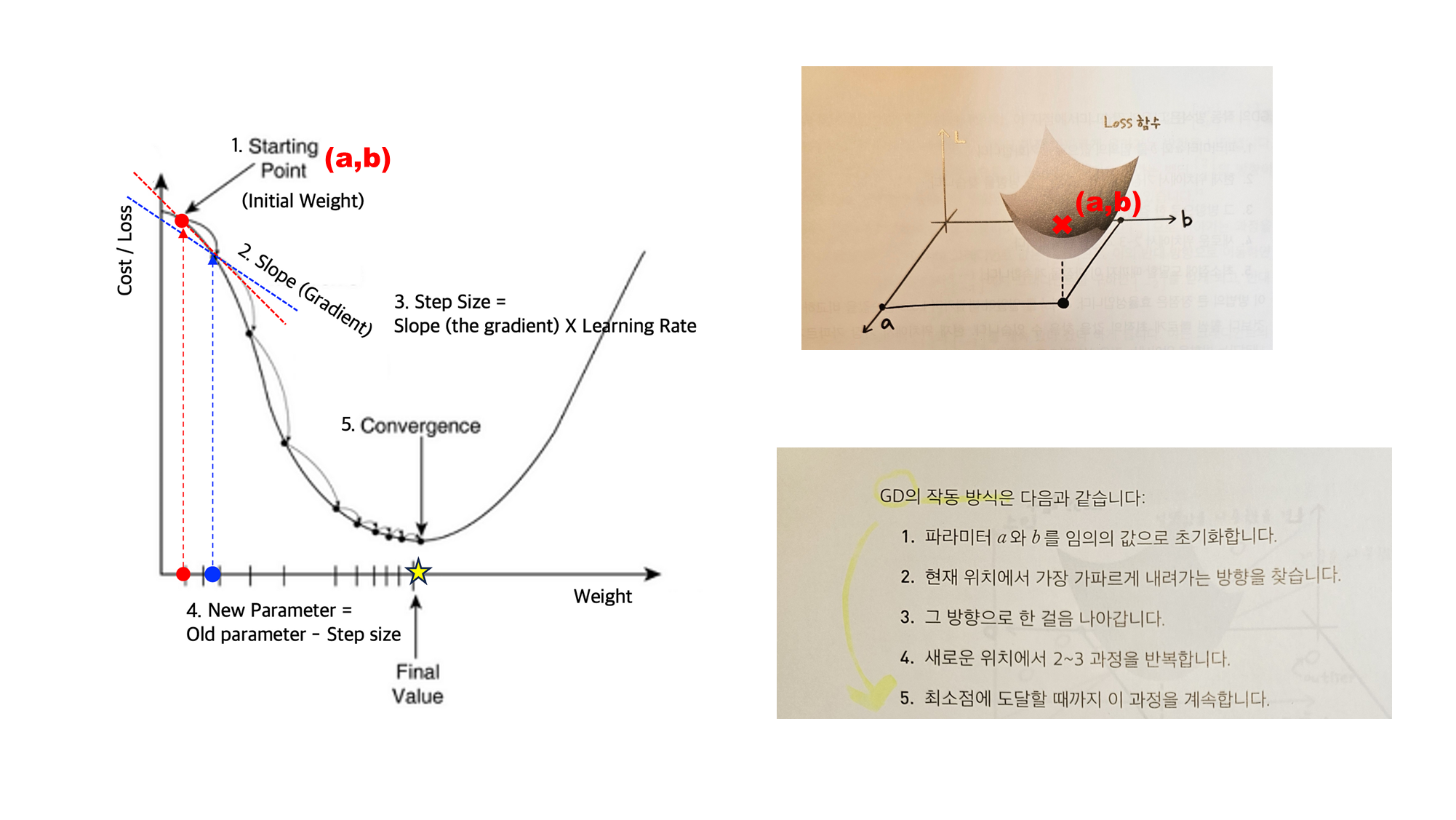
(좌) 혁펜하임 『Easy! 딥러닝』, (상) Gradient Descent, (하) GD 비유 - 등산
위 그림을 가지고 실제 계산 가능한 예시를 살펴보겠습니다.
Ex. 함수 f(x,y)=x2+y2f(x, y) = x^2 + y^2f(x,y)=x2+y2를 생각해 보겠습니다.
- 이 함수는 원점 (0,0)(0,0)(0,0)에서 최소값을 가집니다.
- 즉, 우리가 목표하는 최소값을 찾으려면 원점으로 이동해야 합니다.
1. 그래디언트 계산
- 앞에서 정의했던 것처럼 현재 위치 (x,y)(x, y)(x,y)에서 가장 빠르게 증가하는 방향은 함수 f(x,y)=x2+y2f(x, y) = x^2 + y^2f(x,y)=x2+y2의 편미분 값인 [2x,2y][2x, 2y][2x,2y]입니다.
∇f(x,y)=[∂f∂x,∂f∂y]=[2x,2y]\nabla f(x, y) = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right] = [2x, 2y]∇f(x,y)=[∂x∂f,∂y∂f]=[2x,2y]
- ∇f(x,y)=[2x,2y]\nabla f(x, y) = [2x, 2y]∇f(x,y)=[2x,2y]는 (x,y)(x,y)(x,y)에서 함수가 증가하는 방향을 나타냅니다.
📖 (참고) Gradient Descent의 목표는 Loss Function을 최소화하는 파라미터를 찾는 것입니다.
- 우리가 어떤 최적화 문제를 풀 때, 예를 들어 머신러닝에서는 손실 함수(Loss Function, L(x,y)) 가 있습니다.
- 머신러닝에서는 f(x,y)f(x,y)f(x,y)가 실제로 손실 함수 L(x,y)L(x,y)L(x,y) 역할을 합니다.
- 결국, 우리는 이(f(x,y)f(x,y)f(x,y), L(x,y)L(x,y)L(x,y))를 최소화하는 것을 목적으로 해야합니다.
2. Gradient Descent 수행
- 우리는 손실을 줄이고 싶으므로 그래디언트의 반대 방향으로 이동 해야 합니다.
(x,y)←(x,y)−α⋅∇f(x,y)(x, y) \leftarrow (x, y) - \alpha \cdot \nabla f(x, y)(x,y)←(x,y)−α⋅∇f(x,y)
- 여기서 α\alphaα는 학습률(learning rate)로, 얼마나 크게 이동할지를 결정합니다.
3. 업데이트 과정
- 예를 들어, 초기값이
(1,1)이고 학습률이0.1이면, 업데이트는 다음과 같이 수행됩니다.
x=1−0.1×2(1)=0.8x = 1 - 0.1 \times 2(1) = 0.8x=1−0.1×2(1)=0.8
y=1−0.1×2(1)=0.8y = 1 - 0.1 \times 2(1) = 0.8y=1−0.1×2(1)=0.8
→ 즉, (1,1)에서 (0.8, 0.8)로 이동하면서 손실이 감소 합니다.
💡 (정리) 그래디언트는 함수가 가장 빠르게 증가하는 방향을 가리키므로, 그 반대 방향으로 이동하면 손실을 최소화하는 방향이 됩니다.
2. 최적화 기법이란?
최적화(Optimization)는 머신러닝 및 딥러닝 모델이 손실 함수(Loss Function)를 최소화하기 위해 가중치(Weight)와 편향(Bias)을 조정하는 알고리즘을 의미합니다.
✔ 왜 최적화가 중요한가?
- 모델이 더 나은 예측을 수행하도록 가중치를 조정
- 신경망의 학습 속도를 개선
- 메모리와 연산 비용을 줄이고 효율적으로 학습 가능
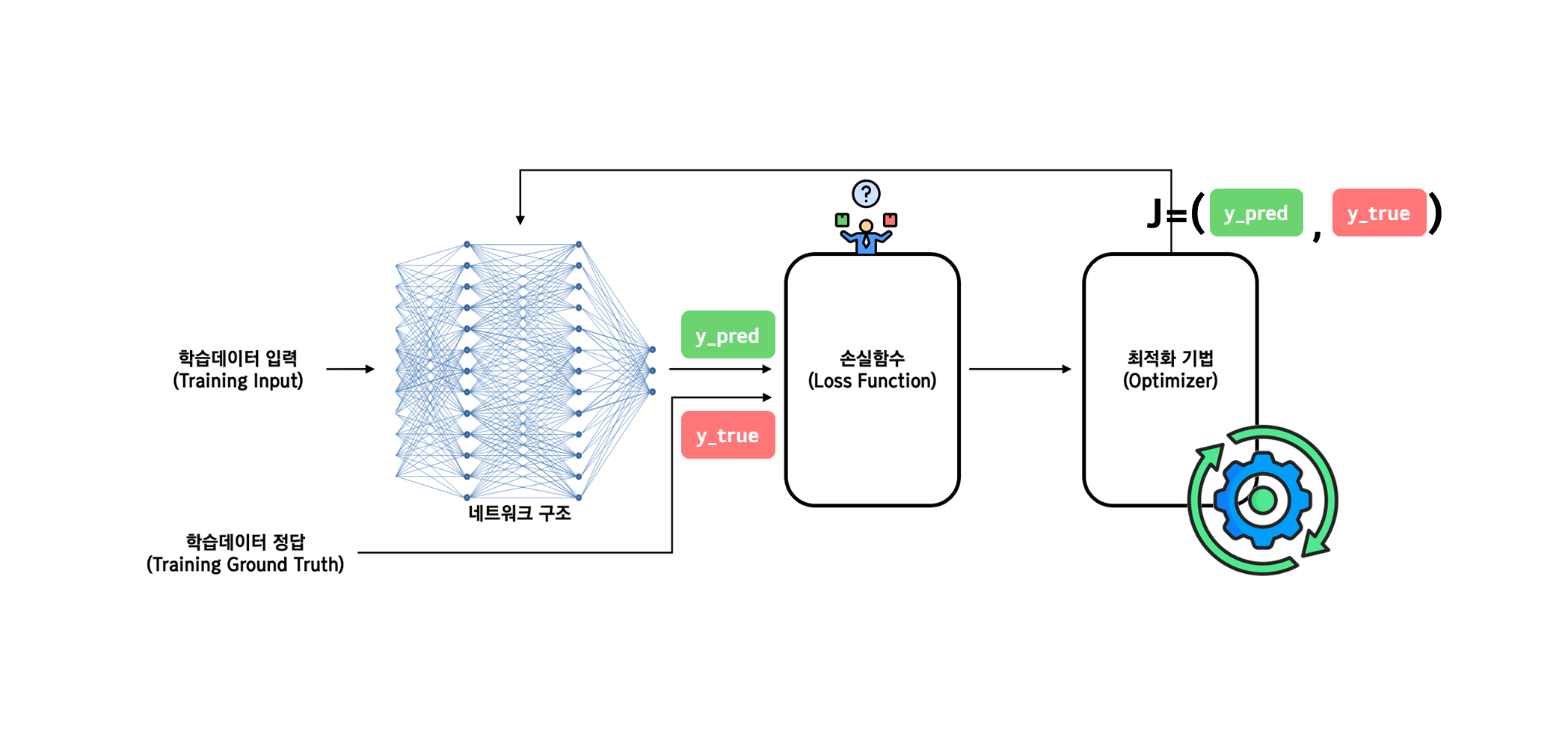
기본적인 최적화 방법으로는 위에서 소개한 가장 기본적인 경사 하강법(Gradient Descent, GD)이 있지만, 다양한 문제점을 극복하기 위해 여러 가지 변형된 방법들이 등장했습니다.
최적화 기법들은 아래와 같은 공통적인 목표를 가지오 있습니다.
💌 최적화 기법들의 공통 목표
- 학습 속도를 높이고 불필요한 연산을 줄이는 것
- 더 빠르고 안정적으로 최적해에 도달하는 것
- 진동을 줄이고 효율적인 방향으로 이동하는 것
🦾 최적화 기법의 발전 과정
초기 Gradient Descent 방식에서 출발하여, 더 효율적인 학습과 안정적인 수렴을 위해 다양한 방법들이 개발되었습니다.
- 최적화 기법은 각각의 문제점을 보완하는 방식으로 점진적으로 발전해왔습니다.
| 최적화 기법 | 등장 배경 | 주요 특징 |
|---|---|---|
| Gradient Descent (GD) | 1847년 Cauchy | 전체 데이터셋을 이용해 안정적으로 학습하지만 연산량이 많음 |
| Stochastic Gradient Descent (SGD) | 1951년 Robbins & Monro | 하나의 샘플만 사용하여 빠르게 학습하지만 진동이 큼 |
| Mini-Batch Gradient Descent | 1980년대 | 전체 데이터와 샘플의 절충안으로 효율적 |
| Momentum | 1964년 Polyak | 진동을 줄이고 더 빠르게 수렴 |
| Nesterov Accelerated Gradient (NAG) | 1983년 Nesterov | Momentum의 개선 버전, 더 빠르게 수렴 |
| AdaGrad | 2011년 Duchi et al. | 희소한 데이터에 강하지만 학습률 감소 문제 |
| RMSProp | 2012년 Hinton | AdaGrad의 문제 해결, 학습률 조절 가능 |
| AdaDelta | 2012년 Zeiler | 학습률 감소 문제 해결, 학습률을 동적으로 조정 |
| Adam | 2014년 Kingma & Ba | Momentum과 RMSProp 결합, 가장 널리 사용됨 |
| NAdam | 2016년 Dozat | Adam에 Nesterov Momentum 추가 |
- 아래 그림은 별도의 참고 자료로 하용호 님의 최적화 방법론 계보 시각화 자료 공유드립니다.
- 한눈에 살펴보기 좋게 정리가 되어 있습니다. (아래 그림 참고) 🙌
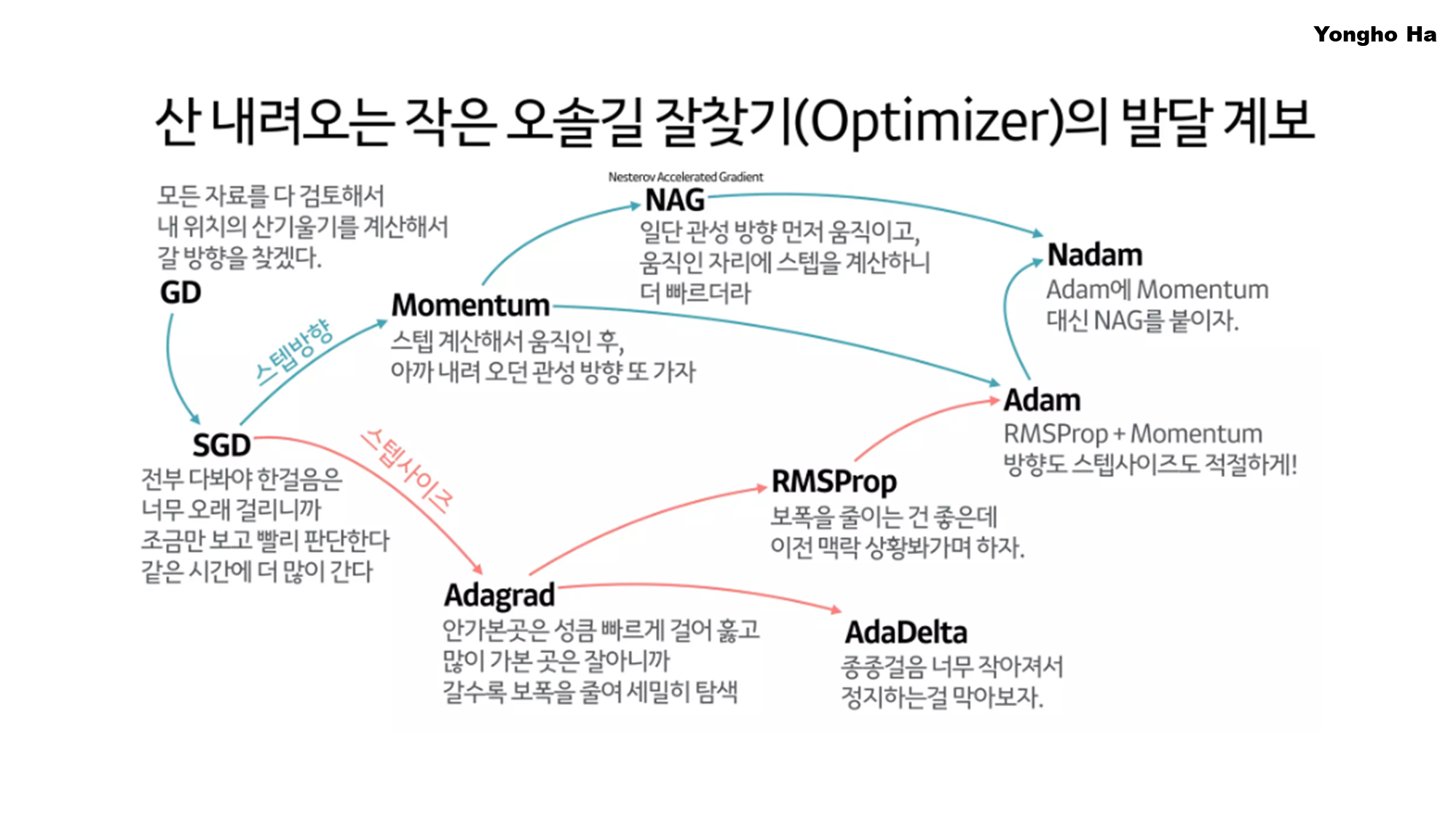
출처: 하용호 님 SlideShare 자료 (https://www.slideshare.net/slideshow/ss-79607172/79607172#49)
이번 포스팅에서 2.5 경사 하강법, 2.7 확률적 경사 하강법, 2.8 Mini-Batch Gradient Descent, 2.8 Mini-Batch Gradient Descent, 2.9 Momentum, 2.10 RMSProp, 그리고 2.11 Adam까지 Optimzier 시리즈를 묶어서 정리 및 살펴보려고 합니다. (+ NAG, AdaGrad, AdaDelta, NAdam 자체 추가)
최적화 기법 정리
1. Gradient Descent(GD, 경사 하강법) - (1847, Cauchy)
배경
Gradient Descent는 미분 가능한 연속 함수의 최적화 문제를 해결하기 위해 19세기 수학자 Augustin-Louis Cauchy에 의해 처음 제안되었습니다.
- 이후 컴퓨터 과학과 머신러닝에서 최적화 문제를 해결하는 핵심 알고리즘이 되었습니다.
기여 (Contribution)
- 미분 가능한 함수의 최적화 방법으로서 손실 함수의 기울기를 기반으로 최소점을 찾는 방법론을 확립.
- 선형 회귀 및 로지스틱 회귀에서 손실 함수를 최적화하는 가장 기본적인 방법.
수식
θt+1=θt−α∇L(θt)\theta_{t+1} = \theta_t - \alpha \nabla L(\theta_t)θt+1=θt−α∇L(θt)
- θt\theta_tθt: ttt번째 업데이트 시점의 파라미터
- α\alphaα: 학습률 (Learning Rate)
- ∇L(θt)\nabla L(\theta_t)∇L(θt): 손실 함수의 기울기

한계
- 모든 데이터를 사용하여 한 번의 업데이트를 수행하므로 연산량이 크고 속도가 느림.
- 데이터셋이 커질수록 학습 속도가 급격히 감소.
-
Stochastic Gradient Descent (SGD, 확률적 경사 하강법) - (1951, Robbins & Monro)
배경
기존 Gradient Descent(GD)의 주요 문제는 전체 데이터셋을 사용해야 하므로 연산량이 많고 업데이트 속도가 느리다는 점이었습니다.
- 이를 해결하기 위해 Stochastic Gradient Descent(SGD)가 도입되었습니다.
기여 (Contribution)
- 랜덤하게 샘플 하나만 선택하여 업데이트하는 방식으로, 계산량을 크게 줄임.
- 확률적인 특성을 활용하여 지역 최적해(Local Minima)를 벗어나 전역 최적해(Global Minima)로 이동할 가능성을 증가.

수식
θt+1=θt−α∇L(θt;xi)\theta_{t+1} = \theta_t - \alpha \nabla L(\theta_t; x_i)θt+1=θt−α∇L(θt;xi)
- xix_ixi: 랜덤하게 선택된 샘플

한계
- 매 업데이트가 단일 샘플에 의해 결정되므로 진동(Oscillation)이 심할 수 있음.
- 손실 함수가 불안정하게 움직이며 수렴 속도가 일정하지 않음.
-
Mini-Batch Gradient Descent (1980s)
배경
GD와 SGD의 장단점을 절충한 방법으로 등장.
- GD: 안정적인 수렴, 하지만 계산량이 큼.
- SGD: 빠른 업데이트 가능, 하지만 진동이 심함.
기여 (Contribution)
- SGD의 속도와 GD의 안정성을 동시에 확보.
- 전체 데이터를 사용하지 않고 작은 Mini-Batch(미니배치) 단위로 경사를 계산하여 연산량과 안정성을 조절.
수식
θt+1=θt−α∇L(θt;Xmini-batch)\theta_{t+1} = \theta_t - \alpha \nabla L(\theta_t; X_{\text{mini-batch}})θt+1=θt−α∇L(θt;Xmini-batch)
- Xmini-batchX_{\text{mini-batch}}Xmini-batch: 랜덤하게 선택된 미니배치 데이터셋
한계
- 미니배치 크기를 적절히 조정하지 않으면 SGD의 진동 문제나 GD의 느린 속도 문제가 여전히 발생.
-
Momentum (1964, Polyak)
배경
SGD는 업데이트가 불안정하여 손실 함수의 곡률이 급격히 변화할 경우 수렴 속도가 느려지거나 진동이 심해지는 문제가 발생했습니다. 이를 해결하기 위해 물리학에서 사용하는 관성(Inertia) 개념을 도입하여 개선하였습니다.
기여 (Contribution)
- 과거 기울기 방향을 고려하여 진동을 줄이고 수렴 속도를 향상.
- 경사면이 가파르면 더 빠르게 움직이고, 평탄한 구간에서는 속도를 조절함.
수식
vt=βvt−1+(1−β)∇L(θt)v_t = \beta v_{t-1} + (1 - \beta) \nabla L(\theta_t)vt=βvt−1+(1−β)∇L(θt)
θt+1=θt−αvt\theta_{t+1} = \theta_t - \alpha v_tθt+1=θt−αvt
- vtv_tvt: 기울기의 이동 평균 (속도)
- β\betaβ: 모멘텀 계수 (보통 0.9)
한계
- 너무 큰 모멘텀 값은 오버슈팅(Overshooting, 지나친 업데이트) 문제를 유발할 수 있음.
-
Nesterov Accelerated Gradient (NAG) (1983, Nesterov)
배경
Momentum 방식은 기울기가 급격히 변하는 영역에서 부정확한 업데이트를 할 가능성이 있음. NAG는 이를 개선하여 보다 정확한 위치에서 기울기를 계산하는 방식을 도입.
기여 (Contribution)
- 기울기를 계산하기 전에 미리 한 번 업데이트된 위치에서 계산하여 정확도를 높임.
- 수렴 속도를 더욱 빠르게 함.
수식
vt=γvt−1+α∇L(θt−γvt−1)v_t = \gamma v_{t-1} + \alpha \nabla L(\theta_t - \gamma v_{t-1})vt=γvt−1+α∇L(θt−γvt−1)
θt+1=θt−vt\theta_{t+1} = \theta_t - v_tθt+1=θt−vt
한계
- 업데이트가 더욱 정교해지지만, 계산량이 증가.
-
Adagrad (2011, Duchi, Hazan, Singer)
배경
- 학습률이 고정되어 있으면, 어떤 파라미터는 과도하게 업데이트되고 어떤 파라미터는 업데이트가 부족할 수 있음.
- 이를 해결하기 위해 각 파라미터별로 학습률을 조절하는 방법을 도입.
기여 (Contribution)
- 학습률을 개별적으로 조정하여 희소 데이터(Sparse Data)에서 좋은 성능을 보임.
수식
θt+1=θt−αGt+ϵ∇L(θt)\theta_{t+1} = \theta_t - \frac{\alpha}{\sqrt{G_t + \epsilon}} \nabla L(\theta_t)θt+1=θt−Gt+ϵα∇L(θt)
- GtG_tGt: 과거 기울기의 누적합
한계
- 학습률이 계속 감소하여, 나중에는 업데이트가 거의 이루어지지 않는 문제 발생.
-
RMSProp (2012, Hinton)
배경
Adagrad의 학습률 감소 문제를 해결하기 위해 최근의 기울기에 더 큰 가중치를 부여하는 방식으로 개선.
기여 (Contribution)
- 최신 그래디언트에 더 가중치를 두어 Adagrad의 학습 정체 문제를 해결.
수식
E[g2]t=βE[g2]t−1+(1−β)gt2E[g^2]_t = \beta E[g^2]_{t-1} + (1 - \beta) g_t^2E[g2]t=βE[g2]t−1+(1−β)gt2
θt+1=θt−αE[g2]t+ϵgt\theta_{t+1} = \theta_t - \frac{\alpha}{\sqrt{E[g^2]_t + \epsilon}} g_tθt+1=θt−E[g2]t+ϵαgt
한계
- 특정 데이터셋에서는 여전히 학습 속도가 느려질 가능성 존재.
8. Adadelta (2012, Zeiler)
배경
Adagrad의 주요 한계점은 기울기의 제곱합(GtG_tGt)이 계속 커지면서 학습률이 점점 줄어들어 학습이 정체되는 문제였습니다.
Adadelta는 이를 개선하여 학습률이 과도하게 줄어드는 문제를 방지하는 방식을 도입했습니다.
기여 (Contribution)
- Adagrad의 학습률 감소 문제 해결
- 과거 모든 기울기의 정보를 사용하지 않고, 최근의 기울기만 사용하여 학습률을 조절.
- 하이퍼파라미터 α(learning rate)를 제거
- 학습률을 자동으로 조절하여 사용자가 별도로 학습률을 설정하지 않아도 됨.
수식
1) 기울기의 제곱에 대한 이동 평균 유지
E[g2]t=γE[g2]t−1+(1−γ)gt2E[g^2]_t = \gamma E[g^2]_{t-1} + (1 - \gamma) g_t^2E[g2]t=γE[g2]t−1+(1−γ)gt2
2) 업데이트 크기에 대한 이동 평균 유지
E[Δθ2]t=γE[Δθ2]t−1+(1−γ)Δθt2E[\Delta\theta^2]_t = \gamma E[\Delta\theta^2]_{t-1} + (1 - \gamma) \Delta\theta_t^2E[Δθ2]t=γE[Δθ2]t−1+(1−γ)Δθt2
3) 파라미터 업데이트
θt+1=θt−E[Δθ2]t+ϵE[g2]t+ϵgt\theta_{t+1} = \theta_t - \frac{\sqrt{E[\Delta\theta^2]_t + \epsilon}}{\sqrt{E[g^2]_t + \epsilon}} g_tθt+1=θt−E[g2]t+ϵE[Δθ2]t+ϵgt
- γ\gammaγ (보통 0.9) : 과거 기울기의 영향도를 조절하는 감쇠 계수 (decay factor).
- ϵ\epsilonϵ : 수식 안정성을 위한 작은 값.
한계
- 과거의 변화량을 기반으로 학습률을 조정하기 때문에, 빠른 변화가 필요한 경우에는 최적화 속도가 다소 느려질 수 있음.
9. Adam (2014, Kingma & Ba)
배경
Adam(Adaptive Moment Estimation)은 Momentum과 RMSProp을 결합하여 학습률을 조절하는 방식으로 최적화 알고리즘의 단점을 개선한 방법입니다.
- Momentum: 기울기의 이동 평균을 유지하여 진동을 줄이고 빠르게 수렴.
- RMSProp: 학습률을 적응적으로 조절하여 불필요한 업데이트를 방지.
Adam은 이러한 두 가지 개념을 결합하여 학습 속도를 높이면서도 안정성을 유지하는 알고리즘입니다.
기여 (Contribution)
- Momentum + RMSProp의 장점 결합
- 학습률을 동적으로 조절하여 빠르고 안정적인 학습 가능.
- 기울기의 1차(moment)와 2차(moment)를 동시에 고려
- 일반적인 기울기뿐만 아니라 변동성(variance)까지 반영하여 학습률을 조절.
수식
1) 1차 모멘트(기울기의 이동 평균)
mt=β1mt−1+(1−β1)gtm_t = \beta_1 m_{t-1} + (1 - \beta_1) g_tmt=β1mt−1+(1−β1)gt
2) 2차 모멘트(기울기 제곱의 이동 평균)
vt=β2vt−1+(1−β2)gt2v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2vt=β2vt−1+(1−β2)gt2
3) 편향 보정 (Bias Correction)
Adam은 초기 단계에서 mtm_tmt와 vtv_tvt가 0에 가까워지는 문제를 해결하기 위해 보정 계수를 적용합니다.
m^t=mt1−β1t,v^t=vt1−β2t\hat{m}_t = \frac{m_t}{1 - \beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1 - \beta_2^t}m^t=1−β1tmt,v^t=1−β2tvt
4) 최종 업데이트
θt+1=θt−αv^t+ϵm^t\theta_{t+1} = \theta_t - \frac{\alpha}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_tθt+1=θt−v^t+ϵαm^t
하이퍼파라미터
- β1=0.9\beta_1 = 0.9β1=0.9 (보통) → 1차 모멘텀의 감쇠 계수
- β2=0.999\beta_2 = 0.999β2=0.999 (보통) → 2차 모멘텀의 감쇠 계수
- ϵ=10−8\epsilon = 10^{-8}ϵ=10−8 (보통) → 수식 안정성을 위한 작은 값
장점
- 빠르고 안정적인 학습이 가능.
- 하이퍼파라미터 설정에 덜 민감하며 기본 설정으로도 우수한 성능.
- 대부분의 딥러닝 모델에서 기본 옵티마이저로 사용됨.
한계
- 일반 SGD보다 일반화 성능(Generalization)이 떨어질 가능성이 있음.
- 일부 문제에서는 학습률이 지나치게 적응적으로 조정되어 최적해 근처에서 과도한 스텝을 가질 수 있음.
10. Nadam (2016, Dozat)
배경
Adam은 Momentum과 RMSProp을 결합한 방식이지만, Momentum 업데이트가 현재 위치에서 기울기를 계산한 후 이동하는 방식이라 최적 경로를 정확히 예측하기 어렵습니다.
이를 해결하기 위해 Nesterov Accelerated Gradient (NAG)의 개념을 Adam에 추가한 것이 Nadam(Nesterov-accelerated Adaptive Moment Estimation)입니다.
기여 (Contribution)
- Adam의 학습률 조절과 NAG의 예측 기능을 결합하여 더욱 빠른 수렴 가능.
- 기울기를 계산하기 전에 먼저 이동하여 최적해에 도달하는 속도를 높임.
수식
1) 기존의 Adam 업데이트와 비교
Adam의 업데이트:
θt+1=θt−αv^t+ϵm^t\theta_{t+1} = \theta_t - \frac{\alpha}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_tθt+1=θt−v^t+ϵαm^t
Nadam의 업데이트:
θt+1=θt−αv^t+ϵ(β1m^t+(1−β1)gt)\theta_{t+1} = \theta_t - \frac{\alpha}{\sqrt{\hat{v}_t} + \epsilon} (\beta_1 \hat{m}_t + (1 - \beta_1) g_t)θt+1=θt−v^t+ϵα(β1m^t+(1−β1)gt)
즉, 기존의 Adam에서 모멘텀을 조금 더 앞당겨 반영하여 이동하는 방식입니다.
장점
- Adam보다 더 빠르고 안정적으로 수렴.
- 특히, 곡률이 큰 영역에서 더욱 효과적.
한계
- Adam과 마찬가지로, 일반화 성능이 떨어질 가능성이 있음.
- 일부 문제에서는 Adam과 큰 차이가 나지 않을 수도 있음.
결론
현재 딥러닝에서는 Adam이 가장 널리 사용되며, 특정 문제에 따라 RMSProp, Nadam 등이 사용됩니다.
각 최적화 알고리즘은 이전 알고리즘의 한계를 해결하면서 발전해왔으며, 앞으로도 새로운 방식이 연구될 것입니다.
💡 본 게시글은 혁펜하임의 <Easy! 딥러닝> 책의 리뷰어 활동으로 작성되었습니다.
- 도서 구매 링크 1 (교보문고): https://product.kyobobook.co.kr/detail/S000214848175
- 도서 구매 링크 2 (출판사 자사몰): https://shorturl.at/yqZpW