수학 개념정리 차원축소

[개념] 인공지능을 위한 선형대수 : 행렬편

Posted by Euisuk's Dev Log on September 24, 2024

1. 행렬(Matrix)의 정의

인공지능 및 기계 학습에서 행렬(matrix)은 데이터를 처리하고 표현하는 중요한 도구입니다. 행렬은 수를 직사각형 형태로 배열한 것으로, 데이터를 수학적으로 다루기 위해 필수적입니다. 행렬을 사용하면 대규모 데이터를 효율적으로 관리하고 계산할 수 있습니다.

예시:

우리가 이미 익숙한 데이터 테이블을 생각해봅시다.
학생들의 수학 및 영어 성적을 나타내는 데이터가 있다고 가정할 때, 이를 행렬로 표현할 수 있습니다.

A=[908578928876]A = \begin{bmatrix} 90 & 85 \ 78 & 92 \ 88 & 76 \end{bmatrix}A=⎣⎢⎡​907888​859276​⎦⎥⎤​

여기서 행은 학생, 열은 과목(수학과 영어)을 나타냅니다. 이처럼 행렬은 2차원 데이터를 매우 간단하게 표현할 수 있습니다.

행렬을 다룰 때 중요한 개념으로 행렬의 곱셈, 역행렬, 전치 행렬 등이 있으며, 이는 인공지능 모델을 구현할 때 필수적인 기초 연산입니다.

1.1. 행렬의 곱셈(Matrix Multiplication)

행렬의 곱셈은 두 행렬을 곱하는 연산입니다. 두 행렬을 곱하려면 첫 번째 행렬의 열의 개수가 두 번째 행렬의 행의 개수와 같아야 합니다. 곱셈 결과로 나온 행렬의 iii-번째 행과 jjj-번째 열의 값은 첫 번째 행렬의 iii-번째 행과 두 번째 행렬의 jjj-번째 열에 있는 원소들의 곱을 모두 더한 값입니다.

예시:

A=[1234],B=[5678]A = \begin{bmatrix} 1 & 2 \ 3 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} 5 & 6 \ 7 & 8 \end{bmatrix}A=[13​24​],B=[57​68​]

두 행렬을 곱하면,

AB=[(1×5)+(2×7)(1×6)+(2×8)(3×5)+(4×7)(3×6)+(4×8)]=[19224350]AB = \begin{bmatrix} (1 \times 5) + (2 \times 7) & (1 \times 6) + (2 \times 8) \ (3 \times 5) + (4 \times 7) & (3 \times 6) + (4 \times 8) \end{bmatrix} = \begin{bmatrix} 19 & 22 \ 43 & 50 \end{bmatrix}AB=[(1×5)+(2×7)(3×5)+(4×7)​(1×6)+(2×8)(3×6)+(4×8)​]=[1943​2250​]

1.2. 역행렬(Inverse Matrix)

역행렬은 어떤 행렬을 곱했을 때 결과가 단위행렬(identity matrix)이 되는 행렬을 의미합니다. 행렬 AAA에 대해 역행렬을 A−1A^{-1}A−1라고 표기하며, 다음 관계식을 만족합니다.

AA−1=A−1A=IA A^{-1} = A^{-1} A = IAA−1=A−1A=I

단, 모든 행렬에 역행렬이 존재하는 것은 아니며, 행렬식(determinant)이 0이 아닌 경우에만 역행렬이 존재합니다.

예시:
행렬 A=[1234]A = \begin{bmatrix} 1 & 2 \ 3 & 4 \end{bmatrix}A=[13​24​]의 역행렬은,

A−1=1(1×4−2×3)[4−2−31]=[−211.5−0.5]A^{-1} = \frac{1}{(1 \times 4 - 2 \times 3)} \begin{bmatrix} 4 & -2 \ -3 & 1 \end{bmatrix} = \begin{bmatrix} -2 & 1 \ 1.5 & -0.5 \end{bmatrix}A−1=(1×4−2×3)1​[4−3​−21​]=[−21.5​1−0.5​]

1.3. 전치 행렬(Transpose Matrix)

전치 행렬은 원래 행렬의 행과 열을 서로 바꾼 행렬입니다. 행렬 AAA의 전치 행렬은 ATA^TAT로 표기하며, AAA의 첫 번째 행이 ATA^TAT의 첫 번째 열이 되고, 두 번째 행이 두 번째 열이 되는 방식입니다.

예시:
행렬 A=[1234]A = \begin{bmatrix} 1 & 2 \ 3 & 4 \end{bmatrix}A=[13​24​]의 전치 행렬은,

AT=[1324]A^T = \begin{bmatrix} 1 & 3 \ 2 & 4 \end{bmatrix}AT=[12​34​]

2. 고윳값(Eigenvalue)과 고유벡터(Eigenvector)란?


출처 : https://rfriend.tistory.com/181

고유벡터(Eigenvector)의 정의

고유벡터는 행렬이 특정 벡터에 작용할 때, 그 벡터의 방향은 변하지 않고 크기만 변화하는 특별한 벡터입니다. 이는 데이터를 분석하고, 차원을 축소하거나, 이미지 처리를 할 때 매우 유용하게 사용됩니다.

  • 고유벡터(Eigenvector)의 크기(length, size)는 정해져 있지 않습니다. 즉, 고유벡터는 방향만을 나타내며, 크기는 그 값에 영향을 미치지 않습니다. 실제로 고유벡터의 크기는 자유롭게 스칼라 배를 해도 여전히 같은 고유벡터로 간주됩니다.

    • 예를 들어, 고유벡터가 v=[12]\mathbf{v} = \begin{bmatrix} 1 \ 2 \end{bmatrix}v=[12​]라면, 2v=[24]2\mathbf{v} = \begin{bmatrix} 2 \ 4 \end{bmatrix}2v=[24​]도 동일한 방향을 가지므로 같은 고유벡터로 취급됩니다.

  • 실제로 고유벡터를 다룰 때는 주로 단위 벡터(normalized vector)로 변환하여, 벡터의 크기를 1로 맞춰 사용하는 경우가 많습니다. 이를 통해 계산의 일관성을 유지하고 해석을 용이하게 합니다.

고윳값(Eigenvalue)의 정의

고윳값은 행렬이 고유벡터에 작용할 때 벡터의 크기를 얼마나 변화시키는지를 나타냅니다. 이 값은 벡터의 방향을 유지한 상태에서 크기만 변화시키는 비율을 의미합니다.

예시로 이해해봅시다:

  • 행렬 A=[2003]A = \begin{bmatrix} 2 & 0 \ 0 & 3 \end{bmatrix}A=[20​03​]에 벡터 v=[10]\mathbf{v} = \begin{bmatrix} 1 \ 0 \end{bmatrix}v=[10​]를 곱해봅시다.

Av=[2003][10]=[20]A \mathbf{v} = \begin{bmatrix} 2 & 0 \ 0 & 3 \end{bmatrix} \begin{bmatrix} 1 \ 0 \end{bmatrix} = \begin{bmatrix} 2 \ 0 \end{bmatrix}Av=[20​03​][10​]=[20​]

  • 이 결과를 보면, 벡터의 방향은 변하지 않았고 크기만 두 배로 커졌습니다.

    • 이때 고유벡터는 v=[10]\mathbf{v} = \begin{bmatrix} 1 \ 0 \end{bmatrix}v=[10​]이고, 고윳값은 2입니다.

고윳값을 구하는 방법

행렬의 고윳값은 다음과 같은 특성 방정식을 통해 구할 수 있습니다:

Av=λvA \mathbf{v} = \lambda \mathbf{v}Av=λv

이를 변형하면,

(A−λI)v=0(A - \lambda I) \mathbf{v} = 0(A−λI)v=0

  • 여기서 III는 단위행렬입니다.

이 방정식에서 행렬 (A−λI)(A - \lambda I)(A−λI)의 행렬식(determinant)을 0으로 두고 고윳값을 구할 수 있습니다.

예시로 고윳값을 구해봅시다:

  • 행렬 A=[4123]A = \begin{bmatrix} 4 & 1 \ 2 & 3 \end{bmatrix}A=[42​13​]의 고윳값을 구해보겠습니다.

특성 방정식을 세우면:

det⁡(A−λI)=det⁡[4−λ123−λ]=(4−λ)(3−λ)−2=0\det(A - \lambda I) = \det\begin{bmatrix} 4-\lambda & 1 \ 2 & 3-\lambda \end{bmatrix} = (4-\lambda)(3-\lambda) - 2 = 0det(A−λI)=det[4−λ2​13−λ​]=(4−λ)(3−λ)−2=0

이를 풀면, 두 개의 고윳값 λ1=5\lambda_1 = 5λ1​=5, λ2=2\lambda_2 = 2λ2​=2를 구할 수 있습니다.

고윳값을 구했다면, 이제 고유벡터(eigenvector)를 구할 차례입니다. 고유벡터는 주어진 고윳값에 대응하는 벡터로, 아래의 과정을 통해 구할 수 있습니다.

고유벡터를 구하는 방법

고유벡터는 행렬 방정식을 통해서 구할 수 있습니다.

  1. 먼저, 고윳값 λ\lambdaλ에 대해 행렬 방정식 (A−λI)v=0(A - \lambda I) \mathbf{v} = 0(A−λI)v=0을 사용합니다.

    • AAA는 원래의 행렬
    • λ\lambdaλ는 고윳값
    • III는 단위 행렬
    • v\mathbf{v}v는 구하려는 고유벡터

  2. 방정식 (A−λI)v=0(A - \lambda I) \mathbf{v} = 0(A−λI)v=0을 풀어서 고유벡터 v\mathbf{v}v를 구합니다.

예시

우리가 구한 고윳값을 사용하는 행렬 AAA는 다음과 같습니다.

A=[4123]A = \begin{bmatrix} 4 & 1 \ 2 & 3 \end{bmatrix}A=[42​13​]

  • 참고로 도출한 고윳값은 λ1=5\lambda_1 = 5λ1​=5, λ2=2\lambda_2 = 2λ2​=2입니다.

1. 첫 번째 고윳값 λ1=5\lambda_1 = 5λ1​=5에 대한 고유벡터 구하기

  • 행렬 AAA에서 첫 번째 고윳값 λ1=5\lambda_1 = 5λ1​=5를 대입하여 A−5IA - 5IA−5I를 계산합니다.

A−5I=[4123]−5[1001]=[4−5123−5]=[−112−2]A - 5I = \begin{bmatrix} 4 & 1 \ 2 & 3 \end{bmatrix} - 5 \begin{bmatrix} 1 & 0 \ 0 & 1 \end{bmatrix} = \begin{bmatrix} 4-5 & 1 \ 2 & 3-5 \end{bmatrix} = \begin{bmatrix} -1 & 1 \ 2 & -2 \end{bmatrix}A−5I=[42​13​]−5[10​01​]=[4−52​13−5​]=[−12​1−2​]

  • 이제 행렬 방정식 (A−5I)v=0(A - 5I) \mathbf{v} = 0(A−5I)v=0을 풀어야 합니다.

[−112−2][v1v2]=[00]\begin{bmatrix} -1 & 1 \ 2 & -2 \end{bmatrix} \begin{bmatrix} v_1 \ v_2 \end{bmatrix} = \begin{bmatrix} 0 \ 0 \end{bmatrix}[−12​1−2​][v1​v2​​]=[00​]

  • 이 행렬 방정식을 풀면, 다음과 같은 연립 방정식을 얻습니다:

−1⋅v1+1⋅v2=0⇒v1=v2-1 \cdot v_1 + 1 \cdot v_2 = 0 \quad \Rightarrow \quad v_1 = v_2−1⋅v1​+1⋅v2​=0⇒v1​=v2​

  • 즉, 첫 번째 고유벡터는 v1=v2v_1 = v_2v1​=v2​이므로, 첫 번째 고유벡터는 다음과 같은 형태가 됩니다:

v1=[11]\mathbf{v}_1 = \begin{bmatrix} 1 \ 1 \end{bmatrix}v1​=[11​]

2. 두 번째 고윳값 λ2=2\lambda_2 = 2λ2​=2에 대한 고유벡터 구하기

  • 두 번째 고윳값 λ2=2\lambda_2 = 2λ2​=2를 대입하여 A−2IA - 2IA−2I를 계산합니다.

A−2I=[4123]−2[1001]=[4−2123−2]=[2121]A - 2I = \begin{bmatrix} 4 & 1 \ 2 & 3 \end{bmatrix} - 2 \begin{bmatrix} 1 & 0 \ 0 & 1 \end{bmatrix} = \begin{bmatrix} 4-2 & 1 \ 2 & 3-2 \end{bmatrix} = \begin{bmatrix} 2 & 1 \ 2 & 1 \end{bmatrix}A−2I=[42​13​]−2[10​01​]=[4−22​13−2​]=[22​11​]

  • 이제 행렬 방정식 (A−2I)v=0(A - 2I) \mathbf{v} = 0(A−2I)v=0을 풀어야 합니다.

[2121][v1v2]=[00]\begin{bmatrix} 2 & 1 \ 2 & 1 \end{bmatrix} \begin{bmatrix} v_1 \ v_2 \end{bmatrix} = \begin{bmatrix} 0 \ 0 \end{bmatrix}[22​11​][v1​v2​​]=[00​]

  • 이 행렬 방정식을 풀면, 다음과 같은 연립 방정식을 얻습니다:

2v1+v2=0⇒v2=−2v12v_1 + v_2 = 0 \quad \Rightarrow \quad v_2 = -2v_12v1​+v2​=0⇒v2​=−2v1​

  • 따라서 두 번째 고유벡터는 v2=−2v1v_2 = -2v_1v2​=−2v1​이므로, 두 번째 고유벡터는 다음과 같은 형태가 됩니다:

v2=[1−2]\mathbf{v}_2 = \begin{bmatrix} 1 \ -2 \end{bmatrix}v2​=[1−2​]

(참고) 아래 사이트에서도 쉽게 행렬 연산 및 고유값 계산하실 수 있습니다!

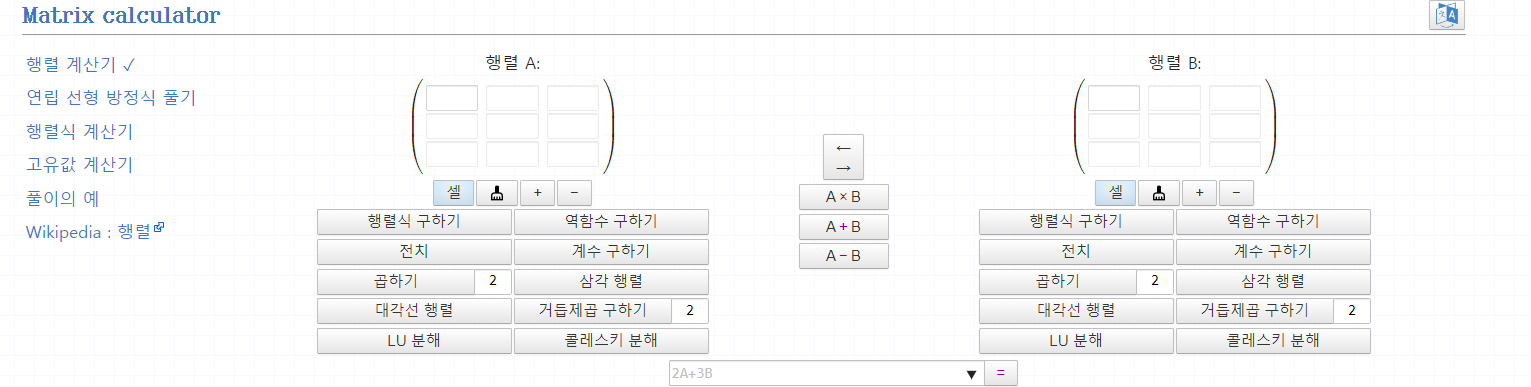
3. 기저(Basis)란?

기저(Basis)는 벡터 공간을 구성하는 기본적인 벡터들의 집합을 의미합니다. 벡터 공간에 있는 모든 벡터는 이 기저 벡터들의 선형 결합(즉, 적절한 배수로 더한 것)으로 표현될 수 있습니다. 기저는 공간의 구조를 결정하는 중요한 개념이며, 기저 벡터들은 선형 독립(linearly independent)이어야 합니다.

기저의 조건:

  1. 선형 독립성: 기저를 구성하는 벡터들은 서로 선형 결합으로 표현될 수 없어야 합니다. 즉, 하나의 기저 벡터는 다른 기저 벡터들의 조합으로 만들어지지 않습니다.
  2. 벡터 공간의 생성(Span): 기저 벡터들을 선형 결합하여 해당 벡터 공간의 모든 벡터를 표현할 수 있어야 합니다.

예시로 이해해봅시다:

  • 2차원 평면에서 가장 기본적인 기저는 e1=[10]\mathbf{e}_1 = \begin{bmatrix} 1 \ 0 \end{bmatrix}e1​=[10​]와 e2=[01]\mathbf{e}_2 = \begin{bmatrix} 0 \ 1 \end{bmatrix}e2​=[01​]입니다.
  • 이 두 벡터는 2차원 공간에서 선형 독립적이고, 이 두 벡터를 적절히 조합하면 2차원 공간의 모든 벡터를 만들 수 있습니다.

v=ae1+be2=a[10]+b[01]=[ab]\mathbf{v} = a\mathbf{e}_1 + b\mathbf{e}_2 = a\begin{bmatrix} 1 \ 0 \end{bmatrix} + b\begin{bmatrix} 0 \ 1 \end{bmatrix} = \begin{bmatrix} a \ b \end{bmatrix}v=ae1​+be2​=a[10​]+b[01​]=[ab​]

즉, e1\mathbf{e}_1e1​과 e2\mathbf{e}_2e2​는 2차원 벡터 공간의 표준 기저(Standard Basis)입니다.

기저의 중요성:

기저는 차원 축소, 고유값 분해, 데이터 변환 등의 다양한 분야에서 중요한 역할을 합니다.

  • 예를 들어, 고유벡터(Eigenvector)는 특정 행렬에서의 고유한 변환 성질을 반영하는 새로운 기저로 사용할 수 있습니다. 이처럼 기저는 우리가 공간을 이해하고 변환하는 데 기본적인 틀을 제공해줍니다.

4. 대각화(Diagonalization)

대각화는 행렬을 그 행렬의 고유벡터(eigenvector)로 구성된 새로운 기저(basis)에서 표현하여, 대각행렬(diagonal matrix)로 변환하는 과정입니다.

  • 대각행렬은 매우 간단한 형태로, 대각선 상에 고윳값들이 배치되고 나머지 원소는 모두 0인 행렬입니다.
  • 이 변환은 행렬의 특성을 더 명확하게 드러내고, 계산을 효율적으로 할 수 있게 해주는 중요한 기법입니다.

대각화를 수학적으로 표현하면 다음과 같습니다:

A=PDP−1A = PDP^{-1}A=PDP−1

여기서,

  • AAA는 대각화하려는 원래의 행렬입니다.
  • PPP는 행렬 AAA의 고유벡터들로 구성된 행렬입니다. PPP의 각 열은 고유벡터로 이루어져 있습니다.
  • DDD는 행렬 AAA의 고윳값들이 대각선에 배열된 대각행렬입니다.
  • P−1P^{-1}P−1는 행렬 PPP의 역행렬입니다.

이 관계식은 행렬 AAA가 고유벡터들로 구성된 새로운 기저에서 대각행렬로 표현될 수 있음을 나타냅니다. 즉, 고유벡터들을 기준으로 원래의 행렬을 변환하면, 단순한 대각행렬로 바뀌어 더 직관적으로 해석할 수 있습니다.

  • 대각화를 직관적으로 설명하면, 복잡한 변환을 단순한 형태로 바꾸는 과정입니다.

예를 들어, 행렬 AAA는 원래 벡터에 복잡한 방식으로 작용하여 방향과 크기를 변화시킬 수 있습니다. 하지만 이 행렬을 고유벡터들의 기저로 변환하면, 행렬 AAA는 대각행렬로 바뀌어 고유벡터 방향으로만 크기를 조정하게 됩니다.

  • 즉, 대각행렬은 각 고유벡터의 방향을 유지하면서 크기만을 변화시키는 변환을 의미합니다.

  • 그 외에도 아래와 같은 장점들이 존재합니다:

    • 계산의 단순화: 대각행렬은 대각선에 위치한 요소들 외에는 모두 0이기 때문에 행렬의 여러 연산, 특히 거듭제곱 같은 복잡한 계산이 매우 간단해집니다.

      An=PDnP−1(∵PP−1=I)A^n = PD^nP^{-1} (∵ PP^{-1}=I)An=PDnP−1(∵PP−1=I)

      여기서 DnD^nDn은 대각행렬의 대각선 요소들만 각각 거듭제곱하면 됩니다.

    • 행렬의 내재된 성질 파악: 행렬을 대각화하면, 고유벡터와 고윳값을 통해 행렬이 데이터에 미치는 변환 효과를 더 직관적으로 파악할 수 있습니다. 이는 차원 축소, 데이터 분석에서 중요한 역할을 합니다.

예시로 대각화를 해봅시다. 행렬 A=[4123]A = \begin{bmatrix} 4 & 1 \ 2 & 3 \end{bmatrix}A=[42​13​]가 주어졌다고 가정합시다.

  • 이 행렬의 고윳값과 고유벡터를 구하면:

    • 고윳값: λ1=5,λ2=2\lambda_1 = 5, \lambda_2 = 2λ1​=5,λ2​=2
    • 고유벡터: v1=[12],v2=[−11]\mathbf{v}_1 = \begin{bmatrix} 1 \ 2 \end{bmatrix}, \mathbf{v}_2 = \begin{bmatrix} -1 \ 1 \end{bmatrix}v1​=[12​],v2​=[−11​]

  • 이 고유벡터들로 구성된 행렬 PPP는:

P=[1−121]P = \begin{bmatrix} 1 & -1 \ 2 & 1 \end{bmatrix}P=[12​−11​]

  • 참고로 PPP의 Inverse(역함수)는:

P−1=[1/31/3−2/31/3]P^{-1} = \begin{bmatrix} 1/3 & 1/3 \ -2/3 & 1/3 \end{bmatrix}P−1=[1/3−2/3​1/31/3​]

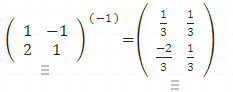
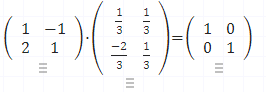
  • 그리고 고윳값을 대각선에 배치한 대각행렬 DDD는:

D=[5002]D = \begin{bmatrix} 5 & 0 \ 0 & 2 \end{bmatrix}D=[50​02​]

  • 이제 대각화된 형태로 표현하면, 다음과 같은 관계식을 얻습니다.

A=PDP−1A = PDP^{-1}A=PDP−1

A=[1−121][5002][1/31/3−2/31/3]A = \begin{bmatrix} 1 & -1 \ 2 & 1 \end{bmatrix} \begin{bmatrix} 5 & 0 \ 0 & 2 \end{bmatrix}\begin{bmatrix} 1/3 & 1/3 \ -2/3 & 1/3 \end{bmatrix}A=[12​−11​][50​02​][1/3−2/3​1/31/3​]

✔️ 대각행렬을 포함한 계산은 아래 특징들 덕분에 일반적인 행렬 곱셈보다 훨씬 간단하고 빠르게 수행할 수 있습니다.

⭐ (추가) 대각행렬 간의 곱셈

  1. 대각 성분만의 곱셈: 두 대각행렬을 곱할 때는 각 대각 성분끼리만 곱하면 됩니다.

    예시:

    (200030004)×(100050002)=(2000150008)\begin{pmatrix} 2 & 0 & 0 \ 0 & 3 & 0 \ 0 & 0 & 4 \end{pmatrix} \times \begin{pmatrix} 1 & 0 & 0 \ 0 & 5 & 0 \ 0 & 0 & 2 \end{pmatrix} = \begin{pmatrix} 2 & 0 & 0 \ 0 & 15 & 0 \ 0 & 0 & 8 \end{pmatrix}⎝⎜⎛​200​030​004​⎠⎟⎞​×⎝⎜⎛​100​050​002​⎠⎟⎞​=⎝⎜⎛​200​0150​008​⎠⎟⎞​

  2. 교환법칙 성립: 대각행렬 간의 곱셈은 교환법칙이 성립합니다.

    예시:

    A=(2003),B=(4005)A = \begin{pmatrix} 2 & 0 \ 0 & 3 \end{pmatrix}, B = \begin{pmatrix} 4 & 0 \ 0 & 5 \end{pmatrix}A=(20​03​),B=(40​05​)

    AB=(80015)=BAAB = \begin{pmatrix} 8 & 0 \ 0 & 15 \end{pmatrix} = BAAB=(80​015​)=BA

  3. 결과도 대각행렬: 두 대각행렬의 곱은 항상 대각행렬이 됩니다.

⭐ (추가) 대각행렬과 일반 행렬의 곱셈

  1. 행 또는 열 단위 곱셈:

    • 대각행렬이 앞에 올 경우: 일반 행렬의 각 행에 대각행렬의 해당 대각 성분이 곱해집니다.
    • 대각행렬이 뒤에 올 경우: 일반 행렬의 각 열에 대각행렬의 해당 대각 성분이 곱해집니다.

    예시:

    D=(200030004),A=(123456789)D = \begin{pmatrix} 2 & 0 & 0 \ 0 & 3 & 0 \ 0 & 0 & 4 \end{pmatrix}, A = \begin{pmatrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 9 \end{pmatrix}D=⎝⎜⎛​200​030​004​⎠⎟⎞​,A=⎝⎜⎛​147​258​369​⎠⎟⎞​

    DA=(246121518283236)DA = \begin{pmatrix} 2 & 4 & 6 \ 12 & 15 & 18 \ 28 & 32 & 36 \end{pmatrix}DA=⎝⎜⎛​21228​41532​61836​⎠⎟⎞​

    AD=(261281524142436)AD = \begin{pmatrix} 2 & 6 & 12 \ 8 & 15 & 24 \ 14 & 24 & 36 \end{pmatrix}AD=⎝⎜⎛​2814​61524​122436​⎠⎟⎞​

⭐ (추가) 대각행렬의 거듭제곱

  • 대각행렬의 k제곱 : 대각행렬의 k제곱은 각 대각 성분을 k제곱하는 것과 같습니다.

    예시:

    (200030004)3=(80002700064)\begin{pmatrix} 2 & 0 & 0 \ 0 & 3 & 0 \ 0 & 0 & 4 \end{pmatrix}^3 = \begin{pmatrix} 8 & 0 & 0 \ 0 & 27 & 0 \ 0 & 0 & 64 \end{pmatrix}⎝⎜⎛​200​030​004​⎠⎟⎞​3=⎝⎜⎛​800​0270​0064​⎠⎟⎞​

5. 닮은 행렬(Similar Matrices)

행렬 AAA와 BBB가 닮았다는 것은 다음과 같은 관계식을 만족한다는 의미입니다:

A=PBP−1A = PBP^{-1}A=PBP−1

닮은 행렬은 동일한 고유 성질을 가지며, 같은 고윳값을 공유합니다.

  • 따라서 닮은 행렬은 행렬식과 대각합이 동일합니다.

💡 행렬식(Determinant): 행렬의 고윳값들의 곱과 동일합니다. 즉, 행렬의 모든 고윳값을 곱한 값이 그 행렬의 행렬식이 됩니다.

💡 대각합(Trace): 행렬의 고윳값들의 합과 동일합니다. 즉, 행렬의 모든 고윳값을 더한 값이 그 행렬의 대각합입니다.

예시:

  • 행렬 A=[4123]A = \begin{bmatrix} 4 & 1 \ 2 & 3 \end{bmatrix}A=[42​13​]와 대각행렬 B=[5002]B = \begin{bmatrix} 5 & 0 \ 0 & 2 \end{bmatrix}B=[50​02​]는 닮은 행렬로, 동일한 고윳값을 가집니다.

6. 직교 대각화(Orthogonal Diagonalization)

직교 대각화(Orthogonal Diagonalization)는 대칭 행렬(symmetric matrix)을 직교 행렬(orthogonal matrix)을 사용하여 대각행렬(diagonal matrix)로 변환하는 과정입니다.

  • 이 과정에서 사용되는 직교 행렬은 대칭 행렬의 고유벡터들로 이루어지며, 대각행렬의 대각선에는 그 행렬의 고윳값들이 위치하게 됩니다.

직교 대각화의 수학적 정의는 다음과 같습니다:

A=QDQTA = Q D Q^TA=QDQT

여기서,

  • AAA: 대칭 행렬.
  • QQQ: 직교 행렬로, 행렬 AAA의 고유벡터(eigenvector)들로 구성됩니다.
  • DDD: 대각행렬로, 행렬 AAA의 고윳값(eigenvalue)들이 대각선에 위치합니다.
  • QTQ^TQT: 행렬 QQQ의 전치 행렬, 직교 행렬의 특성상 Q−1=QTQ^{-1} = Q^TQ−1=QT입니다.

💡 대칭 행렬은 AT=AA^T = AAT=A를 만족하는 행렬로, 행렬의 전치 행렬이 원래의 행렬과 같은 구조입니다.

  • 예를 들어, A=[2113]A = \begin{bmatrix} 2 & 1 \ 1 & 3 \end{bmatrix}A=[21​13​]와 같은 형태입니다.

    • (예시 1) 2x2 대각 행렬: A=[2113],AT=[2113]A = \begin{bmatrix} 2 & 1 \ 1 & 3 \end{bmatrix}, A^T = \begin{bmatrix} 2 & 1 \ 1 & 3 \end{bmatrix}A=[21​13​],AT=[21​13​]
    • (예시 2) 3x3 대각 행렬: B=[423251316],BT=[423251316]B = \begin{bmatrix} 4 & 2 & 3 \ 2 & 5 & 1 \ 3 & 1 & 6 \end{bmatrix}, B^{T} = \begin{bmatrix} 4 & 2 & 3 \ 2 & 5 & 1 \ 3 & 1 & 6 \end{bmatrix}B=⎣⎢⎡​423​251​316​⎦⎥⎤​,BT=⎣⎢⎡​423​251​316​⎦⎥⎤​

💡 직교 행렬은 전치 행렬이 역행렬과 같은 행렬로, QQT=QTQ=IQQ^T=Q^T Q = IQQT=QTQ=I를 만족합니다.

  • 예를 들어, Q=[1212−1212]Q = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}Q=[2​1​−2​1​​2​1​2​1​​]와 같은 형태입니다.

    • (예시 1)
      2x2 직교 행렬 Q=[1212−1212]Q = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}Q=[2​1​−2​1​​2​1​2​1​​]와 QT=[12−121212]Q^T = \begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}QT=[2​1​2​1​​−2​1​2​1​​]에 대하여

      • QTQQ^T QQTQ를 계산하면 단위행렬 III가 나오는 것을 확인할 수 있습니다.

직교 대각화의 특징

  1. 대칭 행렬만 직교 대각화 가능:

    • 대칭 행렬은 항상 직교 대각화가 가능합니다. 즉, 모든 실수 대칭 행렬은 직교 행렬을 사용하여 대각화할 수 있습니다.

  2. 직교 행렬 사용:

    • 직교 대각화에서는 고유벡터들로 이루어진 직교 행렬 QQQ를 사용합니다. 이 행렬은 열벡터들이 서로 직교하고, 각각의 길이가 1인 단위 벡터로 이루어져 있습니다.

  3. 대각행렬의 고윳값:

    • 대각화된 행렬 DDD의 대각선에는 원래 행렬 AAA의 고윳값들이 배치됩니다.

  4. 고유벡터들의 직교성:

    • 대칭 행렬의 고유벡터들은 서로 직교(orthogonal)합니다. 이는 직교 대각화가 가능하게 하는 중요한 성질입니다.

7. 특이값 분해 (SVD)

Singular Value Decomposition(SVD, 특이값 분해)는 행행렬을 세 개의 행렬(좌측 특이벡터, 특이값, 우측 특이벡터)의 곱으로 분해하는 강력한 방법입니다. 모든 행렬에 대해 SVD가 가능하다는 점에서 고유값 분해보다 더 일반적인 기법으로, 차원 축소, 추천 시스템, 이미지 압축 등 다양한 분야에 활용됩니다.

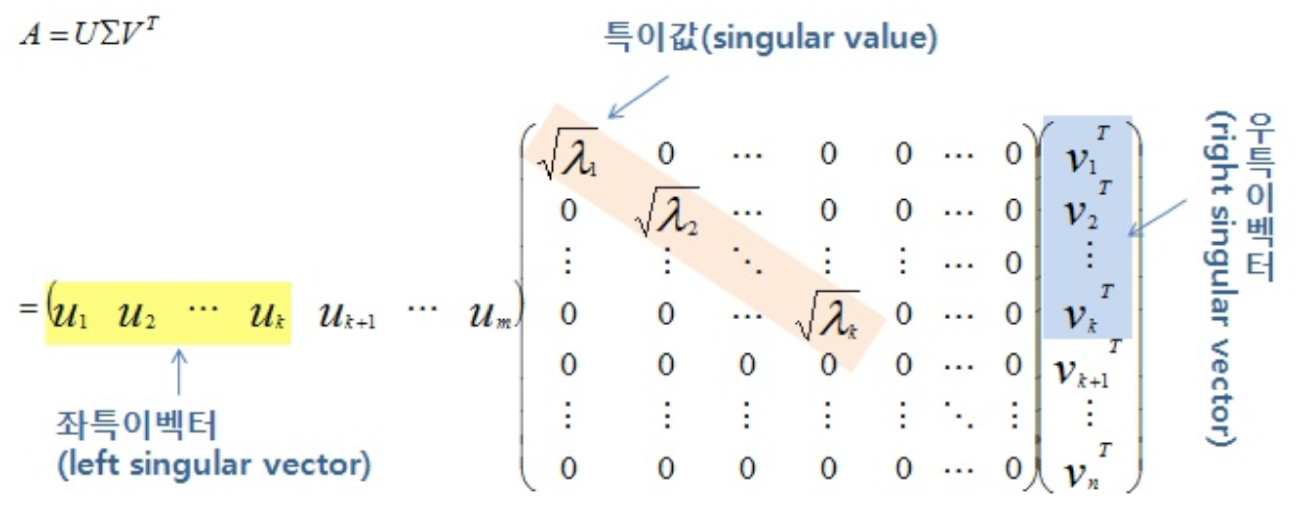
SVD는 다음과 같이 표현됩니다:

A=UΣVTA = U \Sigma V^TA=UΣVT

  • UUU는 AAA의 열 벡터들의 직교 행렬로, 좌측 특이벡터(left singular vector)를 포함합니다.
  • Σ\SigmaΣ는 대각행렬로, 대각선 요소가 행렬 AAA의 특이값(singular values)입니다.
  • VTV^TVT는 AAA의 우측 특이벡터(right singular vector)로 이루어진 행렬입니다.

SVD 분해의 과정

  1. 행렬 ATAA^T AATA와 AATA A^TAAT 구하기

    • SVD 분해를 하기 위해, 먼저 행렬 AAA의 전치 행렬(transpose)를 사용하여 ATAA^T AATA와 AATA A^TAAT를 계산합니다. 이 두 행렬은 각각 우측 특이벡터와 좌측 특이벡터를 구하는 데 사용됩니다.
    • ATAA^T AATA는 n×nn \times nn×n 행렬로, 우측 특이벡터를 구할 때 사용됩니다.
    • AATA A^TAAT는 m×mm \times mm×m 행렬로, 좌측 특이벡터를 구할 때 사용됩니다.

  2. ATAA^T AATA와 AATA A^TAAT의 고유값 및 고유벡터 구하기

    • ATAA^T AATA와 AATA A^TAAT의 고유값(eigenvalue)과 고유벡터(eigenvector)를 구합니다.
    • 이 고유값들은 SVD에서 특이값으로 사용되며, 고유벡터는 특이벡터로 사용됩니다.

  3. 특이값(Singular Value) 구하기

    • ATAA^T AATA와 AATA A^TAAT의 고유값의 제곱근을 구하면 특이값(singular value)이 됩니다. 이 특이값은 대각 행렬 Σ\SigmaΣ의 대각선에 위치하게 됩니다.
    • 특이값은 비음수가 항상 보장되며, 행렬 AAA가 가진 선형 변환의 크기를 나타냅니다.

  4. 우측 특이벡터(Right Singular Vectors) 구하기

    • ATAA^T AATA의 고유벡터들을 구하면, 이 고유벡터들은 SVD에서 우측 특이벡터가 됩니다. 이 고유벡터들을 모아서 직교 행렬 VVV를 만듭니다.
    • 우측 특이벡터는 행렬 AAA의 출력 공간을 정의하는 벡터들입니다.

  5. 좌측 특이벡터(Left Singular Vectors) 구하기

    • AATA A^TAAT의 고유벡터들을 구하면, 이 고유벡터들은 SVD에서 좌측 특이벡터가 됩니다. 이 고유벡터들을 모아서 직교 행렬 UUU를 만듭니다.
    • 좌측 특이벡터는 행렬 AAA의 입력 공간을 정의하는 벡터들입니다.

  6. A=UΣVTA = U \Sigma V^TA=UΣVT로 분해

    • 최종적으로 AAA를 다음과 같이 세 행렬의 곱으로 분해할 수 있습니다:

    A=UΣVTA = U \Sigma V^TA=UΣVT

    • UUU: m×mm \times mm×m 직교 행렬로, 좌측 특이벡터들로 구성됩니다.
    • Σ\SigmaΣ: m×nm \times nm×n 대각 행렬로, 특이값들이 대각선에 위치합니다.
    • VTV^TVT: n×nn \times nn×n 직교 행렬의 전치 행렬로, 우측 특이벡터들로 구성됩니다.

SVD의 응용

  1. 차원 축소: PCA(Principal Component Analysis)와 밀접하게 연관된 SVD는 데이터의 주요 특징을 유지하면서 차원을 축소하는 데 사용됩니다.
  2. 추천 시스템: 넷플릭스 같은 서비스에서 SVD는 사용자 취향을 예측하는 데 중요한 역할을 합니다.
  3. 이미지 압축: 이미지를 표현하는 행렬을 SVD로 분해한 후, 일부 정보만 남겨두고 나머지를 버려 효율적인 압축이 가능합니다.

예시: 2x2 행렬의 SVD

행렬 A=[3223]A = \begin{bmatrix} 3 & 2 \ 2 & 3 \end{bmatrix}A=[32​23​]의 SVD를 계산해봅시다.

  1. ATAA^T AATA 계산:

    ATA=[3223]T[3223]=[13121213]A^T A = \begin{bmatrix} 3 & 2 \ 2 & 3 \end{bmatrix}^T \begin{bmatrix} 3 & 2 \ 2 & 3 \end{bmatrix} = \begin{bmatrix} 13 & 12 \ 12 & 13 \end{bmatrix}ATA=[32​23​]T[32​23​]=[1312​1213​]

  2. AATA A^TAAT 계산:

    AAT=[3223][3223]=[13121213]A A^T = \begin{bmatrix} 3 & 2 \ 2 & 3 \end{bmatrix} \begin{bmatrix} 3 & 2 \ 2 & 3 \end{bmatrix} = \begin{bmatrix} 13 & 12 \ 12 & 13 \end{bmatrix}AAT=[32​23​][32​23​]=[1312​1213​]

  3. 고유값 및 고유벡터 계산:

    • 고유값 λ1=25\lambda_1 = 25λ1​=25, λ2=1\lambda_2 = 1λ2​=1 (고유값의 제곱근이 특이값이 됩니다).
    • 고유벡터는 v1=[11]v_1 = \begin{bmatrix} 1 \ 1 \end{bmatrix}v1​=[11​], v2=[−11]v_2 = \begin{bmatrix} -1 \ 1 \end{bmatrix}v2​=[−11​]입니다.

  4. 특이값으로 대각행렬 Σ\SigmaΣ 만들기:
    특이값의 제곱근을 구하여 Σ\SigmaΣ를 만듭니다.

    Σ=[5001]\Sigma = \begin{bmatrix} 5 & 0 \ 0 & 1 \end{bmatrix}Σ=[50​01​]

  5. 좌측 특이벡터 UUU 구하기:
    좌측 특이벡터 UUU는 AATA A^TAAT의 고유벡터로부터 구해집니다:

    U=[12−121212]U = \begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}U=[2​1​2​1​​−2​1​2​1​​]

  6. 우측 특이벡터 VVV 구하기:
    우측 특이벡터 VVV는 ATAA^T AATA의 고유벡터로부터 구해집니다:

    V=[12−121212]V = \begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}V=[2​1​2​1​​−2​1​2​1​​]

  7. 최종 분해:
    이제 행렬 AAA를 다음과 같이 분해할 수 있습니다.

    A=UΣVT=[12−121212][5001][1212−1212]A = U \Sigma V^T = \begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} 5 & 0 \ 0 & 1 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}A=UΣVT=[2​1​2​1​​−2​1​2​1​​][50​01​][2​1​−2​1​​2​1​2​1​​]

결론

고윳값과 고유벡터는 행렬의 중요한 특성을 나타내며, 이를 활용해 대각화와 닮은 행렬 등을 이해할 수 있습니다. 더 나아가 SVD는 모든 행렬에 대해 적용 가능한 분해 방법으로, 데이터 분석, 차원 축소, 이미지 처리 등 인공지능과 데이터 과학 분야에서 널리 사용됩니다. 이 모든 개념들은 복잡한 행렬 연산을 단순화하고, 데이터를 효율적으로 처리하는 데 매우 중요한 역할을 합니다.

이번 시간에는 딥러닝에서 가장 많이 사용되는 선형대수 개념들을 정리해보았습니다. 오랜만에 수식이 많이 들어간 논문들을 읽으려니까 저도 좀 정리가 필요할거 같더라고요…🤗

도움이 되셨길 바라며 글을 마쳐보겠습니다!

CATALOG
    FEATURED TAGS
    개념정리 딥러닝 AI Agent OpenAI Python Paper Review NLP 머신러닝 Conference 꿀팁 강의노트 Tools ChatGPT 환경설정 Prompt Engineering Computer Vision IT지식 트렌드 Transformer Linux RAG LangChain Google 시계열 Vibe Coding NVIDIA PyTorch 수학 비지도학습 이상탐지 CES Claude Gemini Lovable Anthropic 차원축소 Git CIO CNN EXAONE Pandas Visualization LangGraph LG State Space Model Graph Repo Review SK AI Summit Snippet Sora 도서리뷰 Distillation Network Qwen 알고리즘 데이터분석 MCP Ollama NumPy 강화학습 Splunk Velog
    FRIEND SITES