[Graph] 1장. 그래프와 GNN

1. 그래프란?

그래프는 현실 세계의 데이터를 표현하는 중요한 도구로 사용됩니다.
다양한 분야에서 그래프를 활용하여 관계와 구조를 모델링할 수 있습니다.
예시:
- 사회 과학: 소셜 네트워크에서 개인 간의 관계를 그래프로 표현할 수 있습니다. 예를 들어, 페이스북 친구 관계는 노드(사용자)와 에지(친구 관계)로 나타낼 수 있습니다.
- 화학: 원자와 분자 구조를 그래프로 나타낼 수 있습니다. 각 원자는 노드로, 화학 결합은 에지로 표현됩니다.
- 언어학: 문장에서 단어 간의 관계를 그래프로 모델링할 수 있습니다. 각 단어는 노드로, 단어 간의 연관성은 에지로 나타낼 수 있습니다.

2. 그래프의 표현 (Graph Representation)

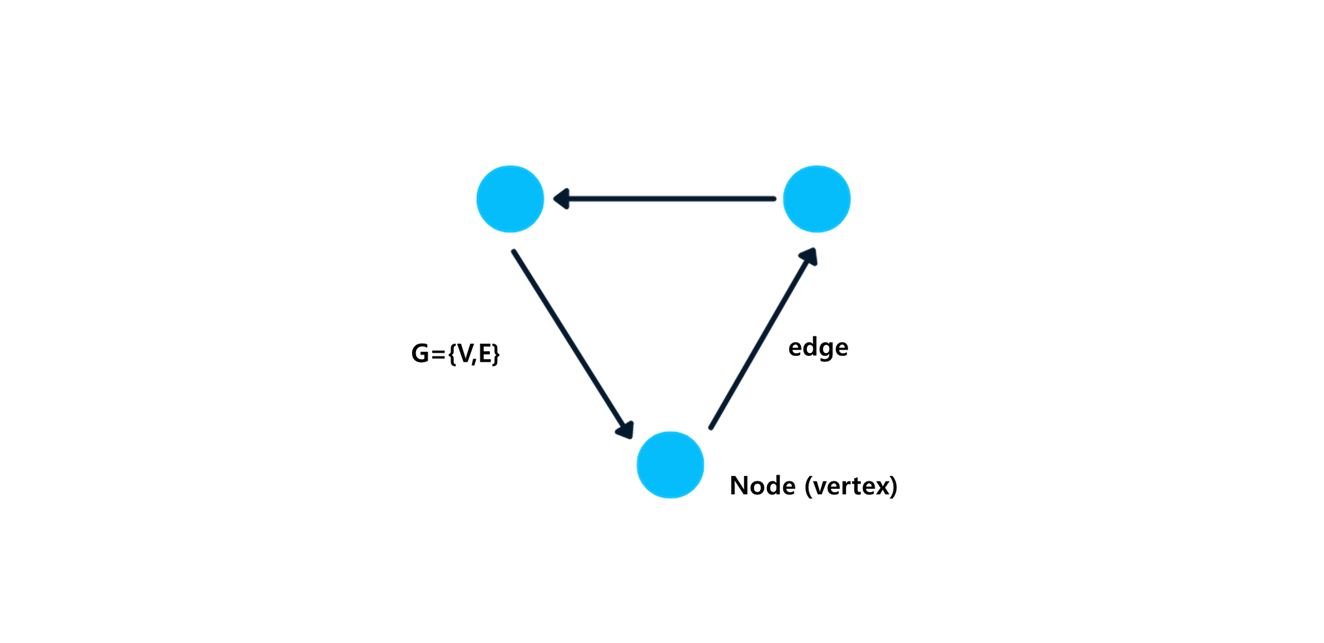
그래프 ( G={V,E}\mathcal{G} = {\mathcal{V}, \mathcal{E}}G={V,E} )는 노드 집합 ( V\mathcal{V}V )와 에지 집합 ( E\mathcal{E}E)로 구성됩니다.

A Graph is the type of data structure that contains nodes and edges. A node can be a person, place, or thing, and the edges define the relationship between nodes. The edges can be directed and undirected based on directional dependencies. - Datacamp

그래프(Graph): 노드와 에지로 구성된 구조로, 노드 간의 관계와 연결을 나타냅니다.
노드(Node): 그래프에서 개별적인 개체를 나타내며, 사용자는 소셜 네트워크의 사용자나 화학에서의 원자 등이 될 수 있습니다.
에지(Edge): 두 노드 간의 연결을 나타내며, 관계나 상호작용을 표현합니다.
그래프 표기 예시:
- 노드와 에지의 관계를 인접 행렬로 나타낼 수 있습니다.

예를 들어, 다음과 같은 인접 행렬이 있을 때:

이는 다음과 같은 그래프를 나타냅니다:

v1v_1v1은 v2v_2v2와 v5v_5v5와 연결
v2v_2v2는 v1v_1v1과 v4v_4v4와 연결
v3v_3v3는 v5v_5v5와 연결
v4v_4v4는 v2v_2v2와 v5v_5v5와 연결
v5v_5v5는 v1v_1v1, v3v_3v3, v4v_4v4와 연결

3. 그래프의 속성 및 측정 (Graph Properties and Measures)

그래프의 다양한 속성과 이를 측정하는 방법이 있습니다.

✔️ 차수(Degree): 노드에 연결된 에지의 수입니다.

CD(v)=deg(v)C_D(v) = \text{deg}(v)CD(v)=deg(v)

예시: v1v_1v1의 차수는 2입니다. (두 개의 에지 e1e_1e1과 e5e_5e5에 연결)

✔️ 이웃(Neighbor): 노드와 직접 연결된 다른 노드들입니다.

예시: v1v_1v1의 이웃은 v2v_2v2와 v5v_5v5입니다.

✔️ 경로(Path): 노드와 에지를 번갈아 나열하여 시작 노드에서 끝 노드로 가는 연결입니다.

예시: v1v_1v1에서 v3v_3v3로 가는 경로는 v1→v5→v3v_1 \to v_5 \to v_3v1→v5→v3입니다.

✔️ 보행(Walk): Walk는 노드와 에지를 번갈아 나열한 순서열로, 각 에지는 바로 앞뒤의 노드와 연결되어 있습니다.

Walk는 Closed Walk와 Open Walk로 나뉘게 됩니다.
- Closed Walk: 시작 노드와 끝나는 노드가 같은 경우(start_node = end_node)를 의미한다.
- Open Walk : 시작 노드와 끝나는 노드가 같지 않는 경우(start_node ≠ end_node)를 의미합니다.
예시:

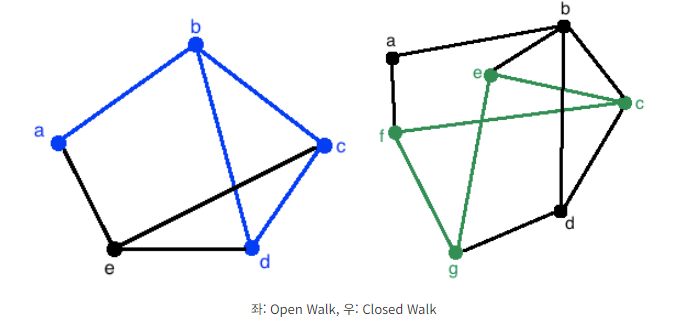
그림 출처 : https://ok-lab.tistory.com/245

위 그림에서 Open Walk와 Closed Walk를 다음과 같이 표현할 수 있습니다:

왼쪽 그림: Open Walk (열린 보행) (a,ab,b,bc,c,cd,d,db,b)(a, ab, b, bc, c, cd, d, db, b)(a,ab,b,bc,c,cd,d,db,b)
이는 노드 a에서 시작하여 노드 d에서 끝나는 열린 보행을 나타냅니다. 각 단계에서 노드와 에지를 번갈아 표시했습니다.
오른쪽 그림: Closed Walk (닫힌 보행), (e,ec,c,cf,f,fg,g,ge,e)(e, ec, c, cf, f, fg, g, ge, e)(e,ec,c,cf,f,fg,g,ge,e)
이는 노드 e에서 시작하여 다시 e로 돌아오는 닫힌 보행을 나타냅니다. 시작 노드와 끝 노드가 같은 것이 특징입니다.

이러한 표현 방식에서:

각 노드는 그 자체로 표시됩니다 (예: a, b, c, …)
각 에지는 연결하는 두 노드의 이름을 붙여 표시합니다 (예: ab는 a와 b를 연결하는 에지)

Walk를 좀 더 구분지어보면, Trail과 Path로 정의할 수 있습니다:

Trail
- 정의: Trail은 에지가 반복되지 않는 Walk입니다.
- 특징: Trail에서는 노드의 반복은 허용되지만, 에지의 반복은 허용되지 않습니다.
- 예시: v1→e1→v2→e2→v3→e3→v2v_1 \to e_1 \to v_2 \to e_2 \to v_3 \to e_3 \to v_2v1→e1→v2→e2→v3→e3→v2
Path
- 정의: Path는 노드가 반복되지 않는 Walk입니다. 따라서 Path는 Trail의 특별한 경우입니다.
- 특징: Path에서는 노드와 에지 모두 반복되지 않습니다.
- 예시: v1→e1→v2→e2→v3v_1 \to e_1 \to v_2 \to e_2 \to v_3v1→e1→v2→e2→v3
관계 (Walk ⊇ Trail ⊇ Path)
- 모든 Path는 Trail이며, 모든 Trail은 Walk입니다.
- 그러나 모든 Walk가 Trail인 것은 아니며, 모든 Trail이 Path인 것도 아닙니다.

💡 어? 근데 일반 경로를 표현할때도 Path라는 말을 쓰던데?
그래프 이론을 다룰 때, 때로는 “Path”라는 용어가 좀 더 일반적인 의미로 사용되어 Walk나 Trail을 포함하는 경우도 있습니다. 그러나 엄밀한 정의에 따르면, Path는 노드의 반복이 없는 가장 제한적인 형태의 Walk입니다.

✔️ 부분 그래프(Subgraph): 주어진 그래프 G=V,E\mathcal{G} = {\mathcal{V}, \mathcal{E}}G=V,E의 부분 그래프 G′=V′,E′\mathcal{G’} = {\mathcal{V’}, \mathcal{E’}}G′=V′,E′는 노드 집합 V′⊆V\mathcal{V’} \subseteq \mathcal{V}V′⊆V와 에지 집합 E′⊆E\mathcal{E’} \subseteq \mathcal{E}E′⊆E로 구성된 그래프입니다. 또한 V′\mathcal{V’}V′는 E′\mathcal{E’}E′의 모든 노드를 포함해야 합니다.

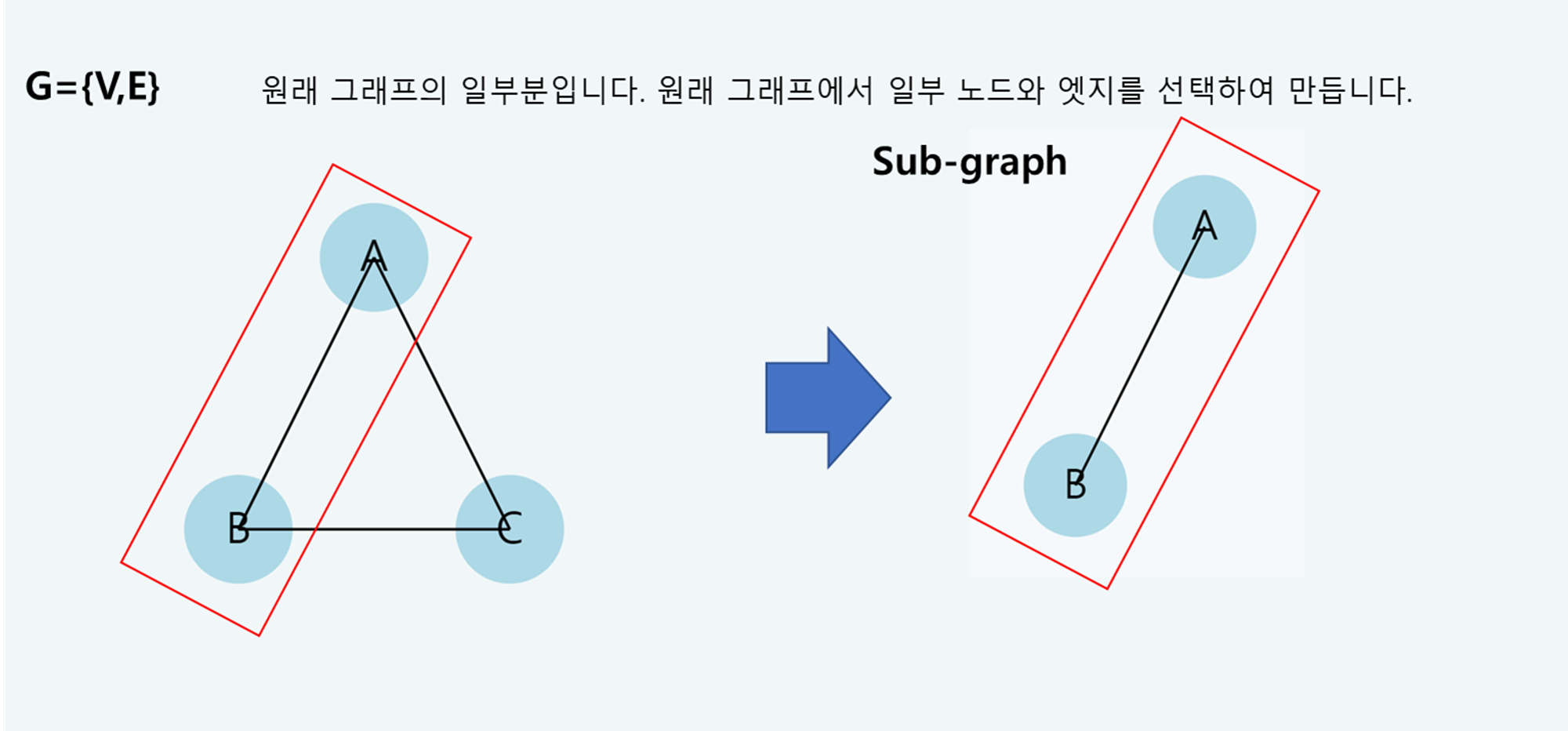
예시: 원본 그래프에서 일부 노드와 에지를 선택하여 부분 그래프를 형성합니다.

원본 그래프: V=v1,v2,v3,v4,v5\mathcal{V} = {v_1, v_2, v_3, v_4, v_5}V=v1,v2,v3,v4,v5, E=e1,e2,e3,e4,e5\mathcal{E} = {e_1, e_2, e_3, e_4, e_5}E=e1,e2,e3,e4,e5
부분 그래프: V′=v1,v2,v3\mathcal{V’} = {v_1, v_2, v_3}V′=v1,v2,v3, E′=e1,e2\mathcal{E’} = {e_1, e_2}E′=e1,e2

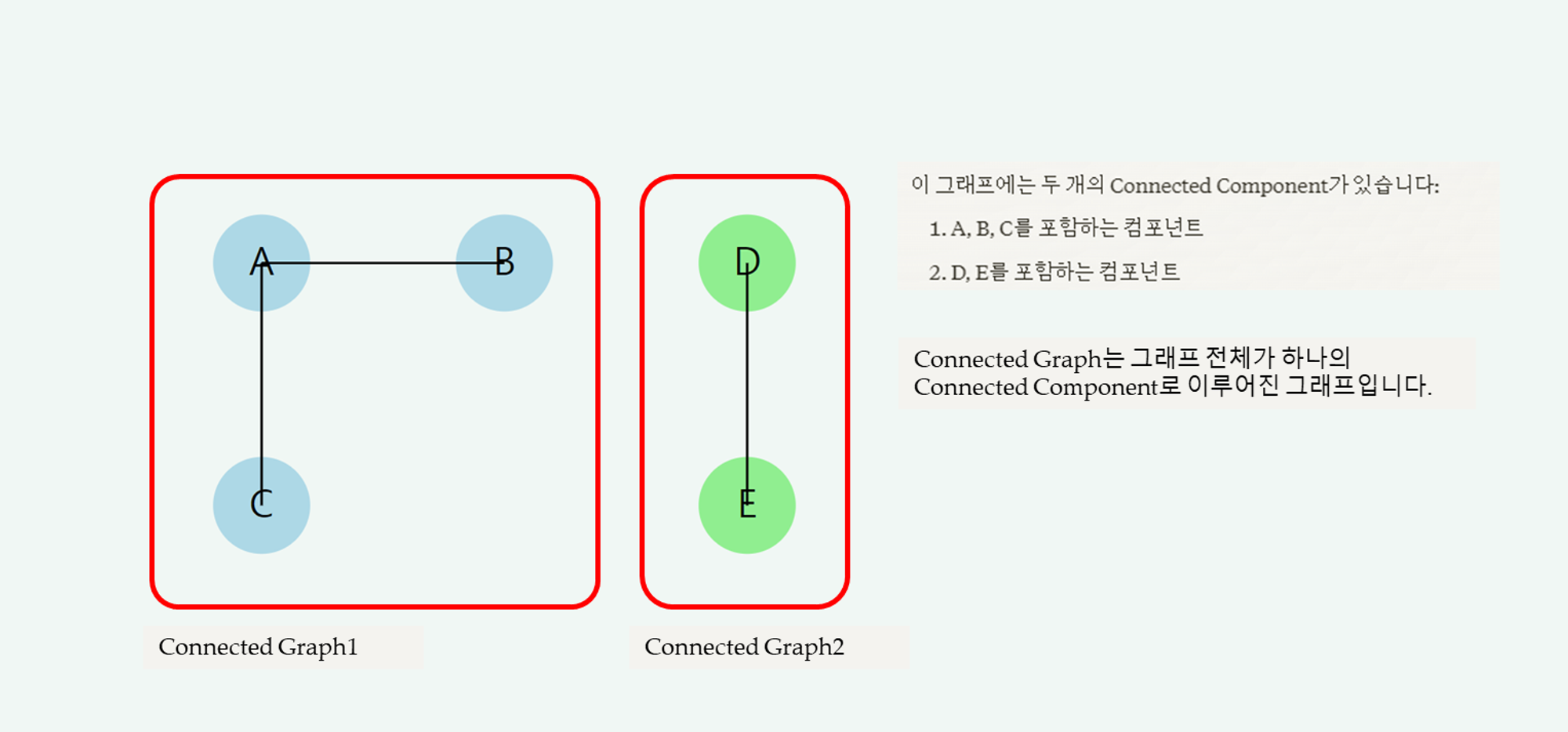
✔️ 연결 성분(Connected Component): 그래프 G=V,E\mathcal{G} = {\mathcal{V}, \mathcal{E}}G=V,E에서, 부분 그래프 G′=V′,E′\mathcal{G’} = {\mathcal{V’}, \mathcal{E’}}G′=V′,E′가 연결 성분이 되려면, G′\mathcal{G’}G′ 내의 모든 노드 쌍 사이에 적어도 하나의 경로가 존재해야 하며, V′\mathcal{V’}V′의 노드들이 V∖V′\mathcal{V} \setminus \mathcal{V’}V∖V′의 노드와 인접하지 않아야 합니다.

연결 성분은 결국, 다음을 의미합니다:
- 연결 성분 내의 모든 노드 사이에 경로가 있어야 함 (내부 연결)
- 연결 성분 내의 노드들이 성분 외부의 노드들과 직접 연결되지 않아야 함 (외부 단절)
예시: 그래프에서 하나의 연결 성분을 찾는 방법은 모든 노드 쌍이 연결되어 있는 하위 그래프를 찾는 것입니다.

✔️ 연결 그래프(Connected Graph): 그래프 G=V,E\mathcal{G} = {\mathcal{V}, \mathcal{E}}G=V,E가 하나의 연결 성분으로 이루어진 경우, 이를 연결 그래프라고 합니다.

예시: 모든 노드가 하나의 연결 성분을 이루는 경우입니다.

✔️ Shortest Path: 두 노드 간의 최단 경로는 두 노드를 연결하는 가장 짧은 경로를 의미합니다.

pstsp=arg⁡min⁡p∈Pst∣p∣p_{st}^{sp} = \arg \min_{p \in P_{st}}

pstsp=argminp∈Pst∣p∣

여기서 PstP_{st}Pst는 노드 sss와 ttt를 연결하는 모든 경로의 집합입니다.

예시:
- v1v_1v1과 v2v_2v2 사이의 최단 경로는 111
- v1v_1v1과 v3v_3v3 사이의 최단 경로는 222

✔️ Diameter: 그래프의 지름은 그래프 내의 모든 최단 경로 중 가장 긴 것을 의미합니다.

diameter(G)=max⁡vs,vt∈Vmin⁡p∈Pst∣p∣\text{diameter}(\mathcal{G}) = \max_{v_s, v_t \in \mathcal{V}} \min_{p \in P_{st}}

diameter(G)=maxvs,vt∈Vminp∈Pst∣p∣

예시: 그래프의 지름은 222로, 이는 최단 경로 중 가장 긴 것이 222라는 것을 의미합니다.

✔️ 중심성(Centrality): 노드의 중요도를 측정하는 여러 가지 방법이 있습니다.

차수 중심성(Degree Centrality):
- 정의: 노드에 연결된 에지의 수를 측정합니다.
- 공식: CD(v)=deg(v)C_D(v) = \text{deg}(v)CD(v)=deg(v)
- 예시: 트위터에서 팔로워 수가 많은 사용자는 차수 중심성이 높습니다.
고유벡터 중심성(Eigenvector Centrality):
- 정의: 노드의 중요도를 해당 노드와 연결된 이웃 노드들의 중요도로 측정합니다.
- 공식: CE(v)=1λ∑u∈neighbors(v)AuvCE(u)C_E(v) = \frac{1}{\lambda} \sum_{u \in \text{neighbors}(v)} A_{uv} C_E(u)CE(v)=λ1∑u∈neighbors(v)AuvCE(u)
  - 여기서 λ\lambdaλ는 고유값, AuvA_{uv}Auv는 노드 uuu와 vvv 사이의 연결을 나타내는 인접 행렬의 값입니다.
- 예시: 페이지랭크(PageRank) 알고리즘은 고유벡터 중심성을 활용하여 웹페이지의 중요도를 평가합니다.
Katz 중심성(Katz Centrality):
- 정의: 고유벡터 중심성의 변형으로, 노드 자체의 중요도를 포함합니다.
- 공식: CK(v)=α∑u∈neighbors(v)AuvCK(u)+βC_K(v) = \alpha \sum_{u \in \text{neighbors}(v)} A_{uv} C_K(u) + \betaCK(v)=α∑u∈neighbors(v)AuvCK(u)+β
  - 여기서 α\alphaα와 β\betaβ는 상수입니다. β=0\beta = 0β=0일 경우, Katz 중심성은 고유벡터 중심성과 동일합니다.
- 예시: 기업 네트워크에서 특정 직급의 중요도를 평가할 때 사용됩니다.
매개 중심성(Betweenness Centrality):
- 정의: 그래프 내에서 특정 노드가 최단 경로를 몇 번이나 지나는지를 측정합니다.
- 공식: CB(v)=∑s≠v≠tσst(v)σstC_B(v) = \sum_{s \neq v \neq t} \frac{\sigma_{st}(v)}{\sigma_{st}}CB(v)=∑s=v=tσstσst(v)
  - 여기서 σst\sigma_{st}σst는 노드 sss에서 ttt로 가는 최단 경로의 수, σst(v)\sigma_{st}(v)σst(v)는 노드 vvv를 지나는 최단 경로의 수입니다.
- 예시: 물류 네트워크에서 중요한 허브 공항은 많은 항공편의 경로에 포함되므로 매개 중심성이 높습니다.

4. 스펙트럴 그래프 이론 (Spectral Graph Theory)

정의: 스펙트럴 그래프 이론은 그래프와 관련된 행렬(주로 인접 행렬이나 라플라시안 행렬)의 고유값(eigenvalues)과 고유벡터(eigenvectors)를 연구하여 그래프의 특성을 이해하고 분석하는 방법론입니다.
목적:
1. 그래프 구조 분석: 그래프의 연결성, 군집 구조, 대칭성 등 복잡한 구조적 특성을 수학적으로 파악합니다.
2. 효율적인 알고리즘 개발: 그래프 분할, 군집화, 랭킹 등 다양한 그래프 관련 문제를 해결하는 효율적인 알고리즘을 개발하는 데 활용됩니다.
3. 그래프 임베딩: 고차원의 그래프 데이터를 저차원 공간으로 매핑하여 시각화하거나 기계 학습에 활용할 수 있게 합니다.
4. 동적 시스템 이해: 그래프 상의 확산 과정이나 랜덤 워크 등 동적 프로세스를 모델링하고 분석합니다.
5. 네트워크 강건성 평가: 네트워크의 취약점이나 중요 노드를 식별하는 데 사용됩니다.
주요 개념:
1. 라플라시안 행렬 (Laplacian Matrix):
  1. L = D - A (D: 차수 행렬, A: 인접 행렬)
  2. 이 행렬의 고유값과 고유벡터가 그래프의 많은 특성을 반영합니다.
2. 스펙트럼 (Spectrum):
  1. 라플라시안 행렬의 고유값 집합
  2. 두 번째로 작은 고유값(Fiedler value)은 그래프의 연결성을 나타냅니다.
  3. 고유값들의 분포는 그래프의 전반적인 구조를 반영합니다.
3. 스펙트럴 군집화 (Spectral Clustering):
  1. 라플라시안의 고유벡터를 사용하여 그래프를 분할하는 기법

5. 그래프 신호 (Graph Signal)

그래프 신호의 정의:
- 그래프 신호는 그래프의 각 노드에 할당된 데이터 값을 의미합니다.
- 수학적 표현: x = [x₁, x₂, …, xₙ], 여기서 n은 노드의 수
- 각 xᵢ는 i번째 노드의 특성(feature) 값을 나타냅니다.
- 이 값은 스칼라(단일 값)이거나 벡터(여러 특성을 포함)일 수 있습니다.
그래프 신호의 의미:
- 노드의 속성이나 상태를 나타냅니다 (예: 소셜 네트워크에서 사용자의 활동량)
- 그래프 구조와 결합하여 복잡한 관계와 패턴을 표현합니다.
그래프 신호 처리 방법:

a) 그래프 푸리에 변환 (GFT):
- 목적: 그래프 신호를 주파수 도메인으로 변환
- 과정: 라플라시안 행렬의 고유벡터를 기저로 사용하여 신호를 분해
- 이점: 그래프 구조를 고려한 주파수 분석 가능
  
  1. 그래프 푸리에 변환 정의: L=UΛUTL = U \Lambda U^TL=UΛUT
  그래프 G\mathcal{G}G의 라플라시안 행렬 LLL의 고유값 분해를 통해 고유벡터 UUU와 고유값 Λ\LambdaΛ를 구합니다.
  
  2. 그래프 신호 xxx의 그래프 푸리에 변환: x^=UTx\hat{x} = U^T xx^=UTx
  여기서 x^\hat{x}x^는 그래프 신호 xxx의 주파수 도메인 표현입니다.
  
  3. 그래프 푸리에 역변환: x=Ux^x = U \hat{x}x=Ux^

b) 그래프 필터링:

목적: 신호의 특정 성분을 강조하거나 제거
방법: 라플라시안의 다항식을 이용한 필터 설계
응용: 노이즈 제거, 특성 추출

c) 그래프 웨이블릿 변환:

목적: 신호의 지역적 특성과 다중 스케일 분석
이점: 국소적인 패턴 탐지와 계층적 구조 분석

d) 그래프 합성곱 (Graph Convolution):

목적: 이웃 노드의 정보를 집계하여 새로운 노드 표현 생성
응용: 그래프 신경망(GNN)의 핵심 연산

e) 그래프 임베딩:

목적: 노드나 그래프 전체를 저차원 벡터로 표현
방법: 랜덤 워크, 행렬 분해, 신경망 등 다양한 기법 사용
응용: 노드 분류, 링크 예측, 그래프 분류 등

f) 스펙트럴 클러스터링:

목적: 그래프의 구조적 특성을 바탕으로 노드 군집화
방법: 라플라시안의 고유벡터를 이용한 차원 축소 및 클러스터링

6. 복잡한 그래프 (Introduction to Complex Graphs)

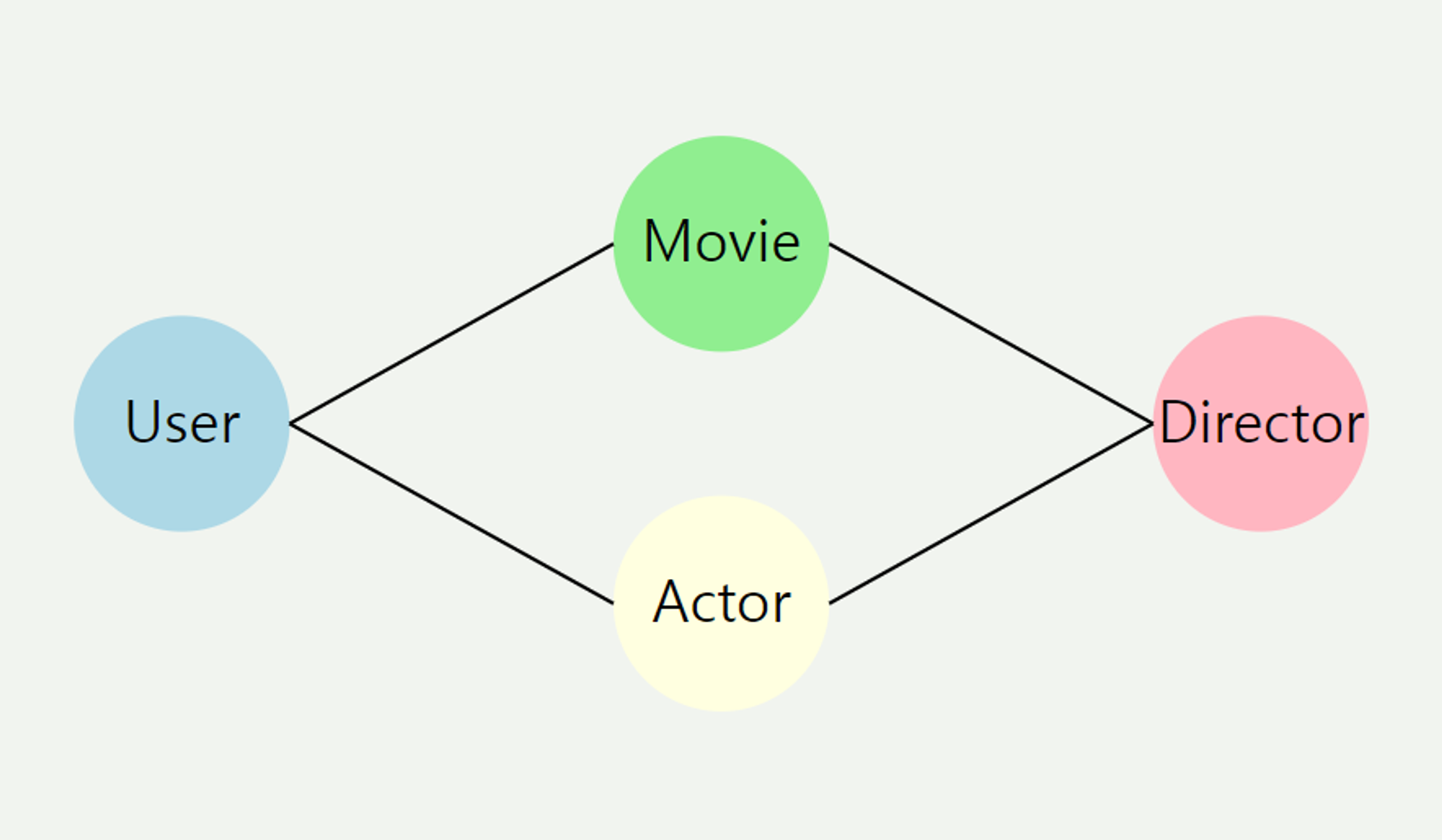
이질 그래프(Heterogeneous Graphs):
- 개념: 여러 종류의 노드와 엣지가 공존하는 그래프입니다.
- 특징:
  - 노드와 엣지가 각각 다른 유형을 가집니다.
  - 복잡한 관계를 표현할 수 있습니다.
- 실생활 예시: 영화 추천 시스템
  - 노드 유형: 사용자, 영화, 배우, 감독
  - 엣지 유형: ‘시청했다’, ‘출연했다’, ‘감독했다’
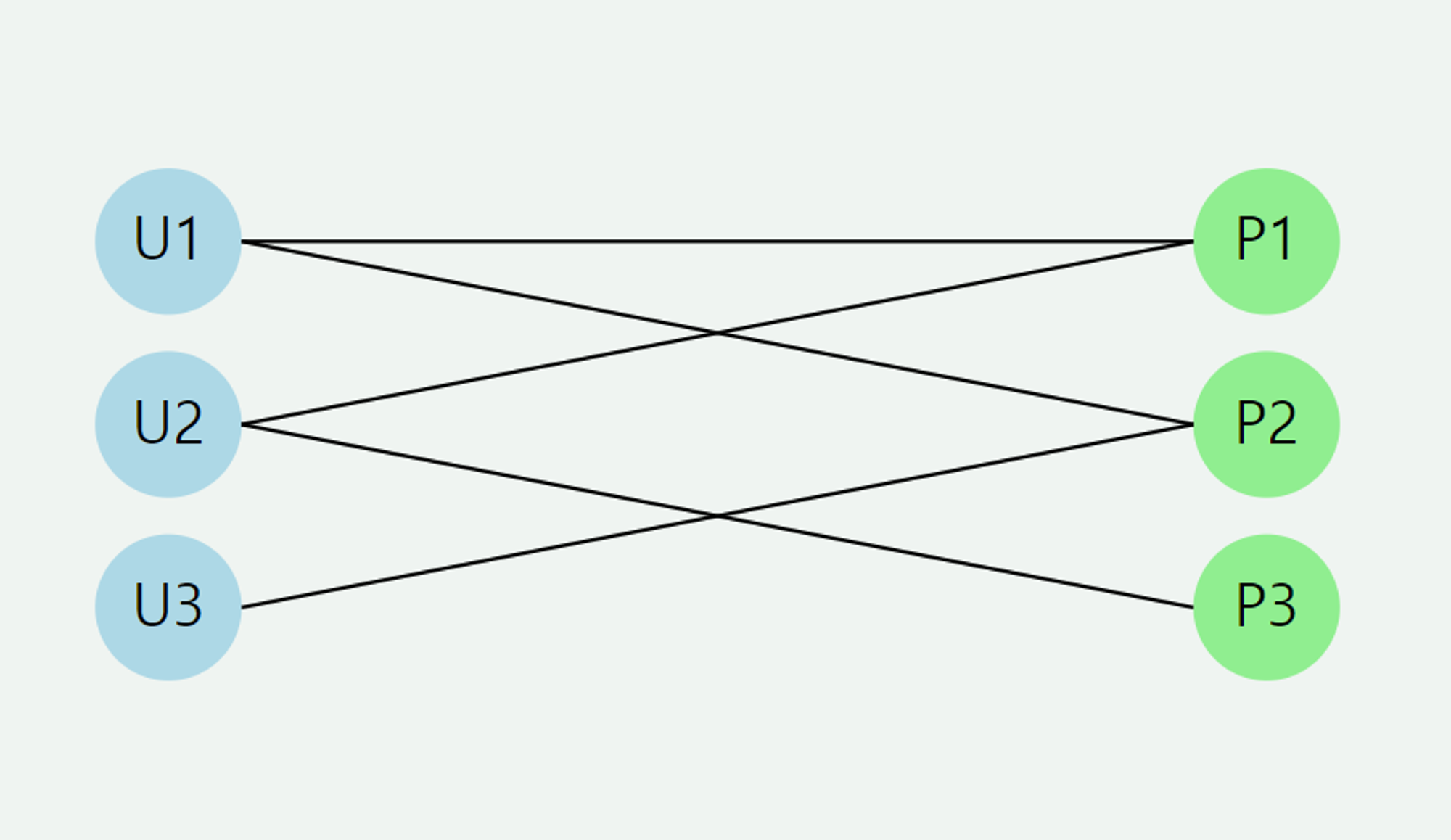
이분 그래프(Bipartite Graphs):
- 개념: 노드를 두 그룹으로 나누고, 같은 그룹 내의 노드 간에는 연결이 없는 그래프입니다.
- 특징:
  - 두 개의 독립적인 노드 집합으로 구성됩니다.
  - 엣지는 항상 서로 다른 집합의 노드를 연결합니다.
- 실생활 예시: 온라인 쇼핑몰의 사용자-상품 관계
  - 노드 그룹 1: 사용자들
  - 노드 그룹 2: 상품들
  - 엣지: ‘구매했다’ 관계
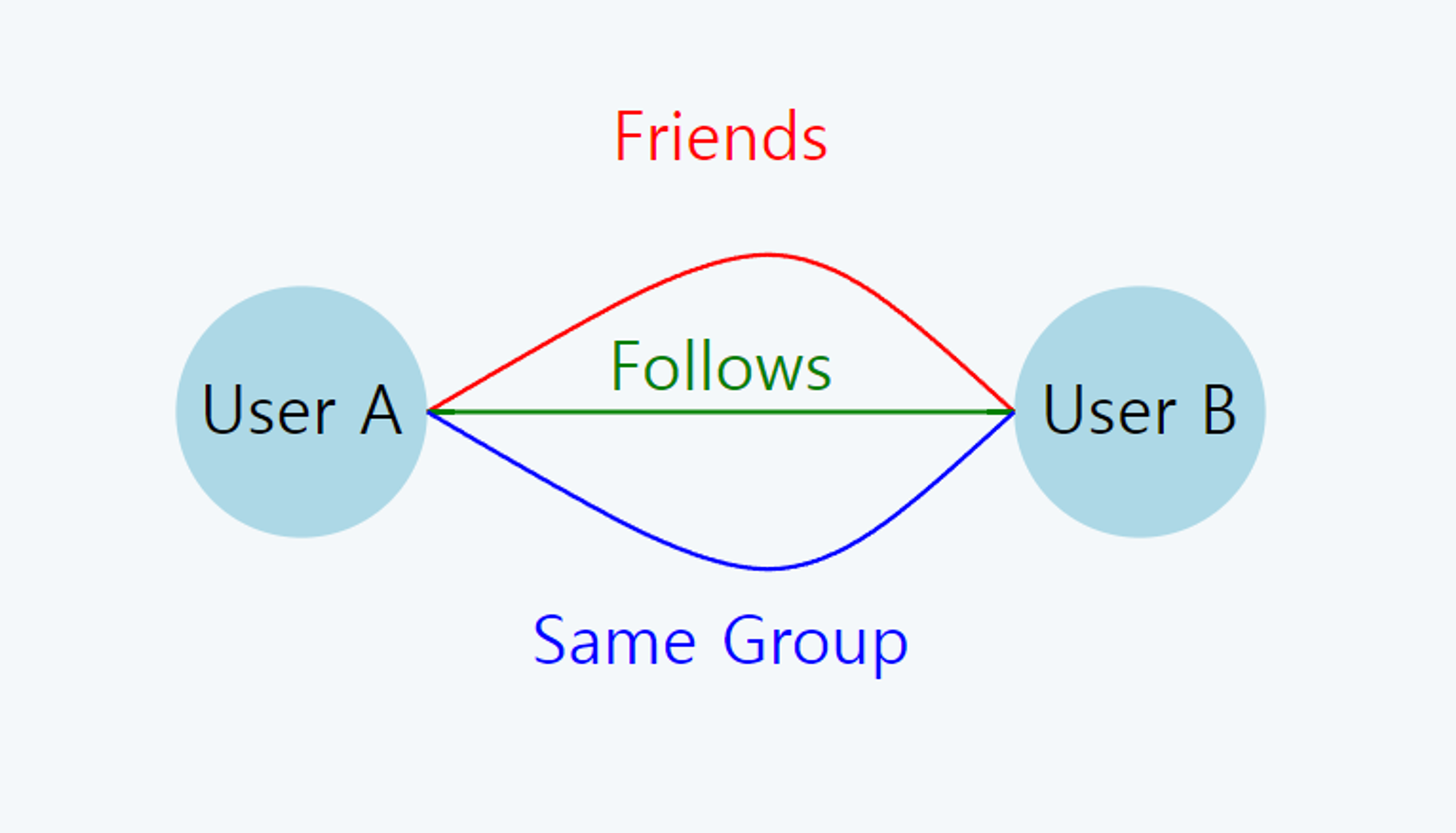
다차원 그래프(Multidimensional Graphs):
- 개념: 노드 간에 여러 종류의 관계가 존재하는 그래프입니다.
- 특징:
  - 같은 노드 쌍 사이에 여러 개의 엣지가 존재할 수 있습니다.
  - 각 엣지는 서로 다른 유형의 관계를 나타냅니다.
- 실생활 예시: 복합적인 소셜 미디어 관계
  - 노드: 사용자들
  - 엣지 유형: ‘친구다’, ‘팔로우한다’, ‘같은 그룹에 속한다’
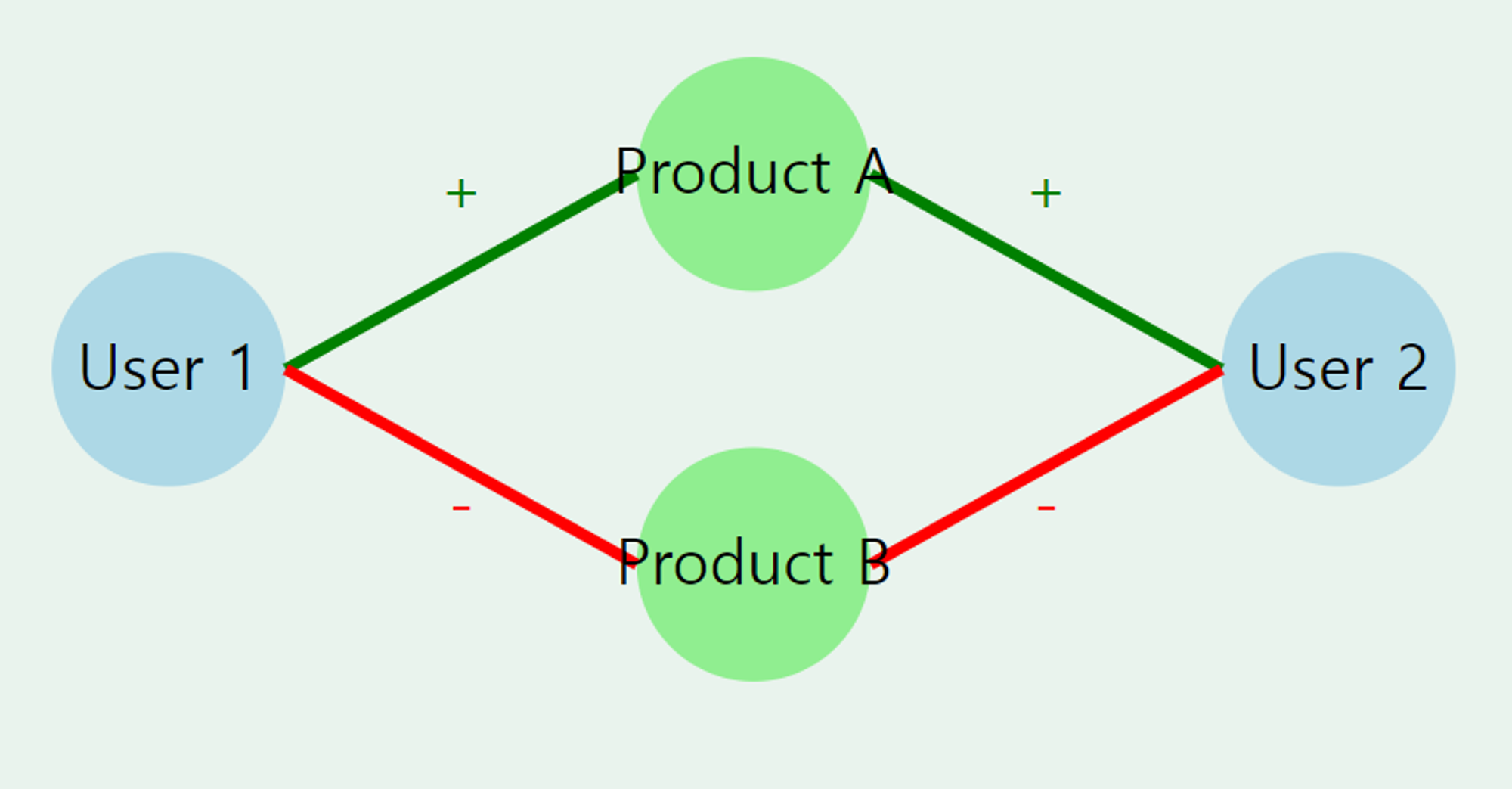
부호화된 그래프(Signed Graphs):
- 개념: 엣지에 양수 또는 음수 값이 할당된 그래프입니다.
- 특징
  - 엣지가 긍정적 또는 부정적 관계를 나타냅니다.
  - 복잡한 사회적 관계나 의견 차이를 모델링하는 데 유용합니다.
- 실생활 예시: 온라인 리뷰 시스템
  - 노드: 사용자, 제품
  - 엣지: 긍정적 리뷰(+), 부정적 리뷰(-)
하이퍼그래프(Hypergraphs):
- 개념: 하나의 엣지(하이퍼엣지)가 두 개 이상의 노드를 연결할 수 있는 그래프입니다.
- 특징:
  - 복잡한 다대다 관계를 표현할 수 있습니다.
  - 전통적인 그래프보다 더 풍부한 관계 표현이 가능합니다.
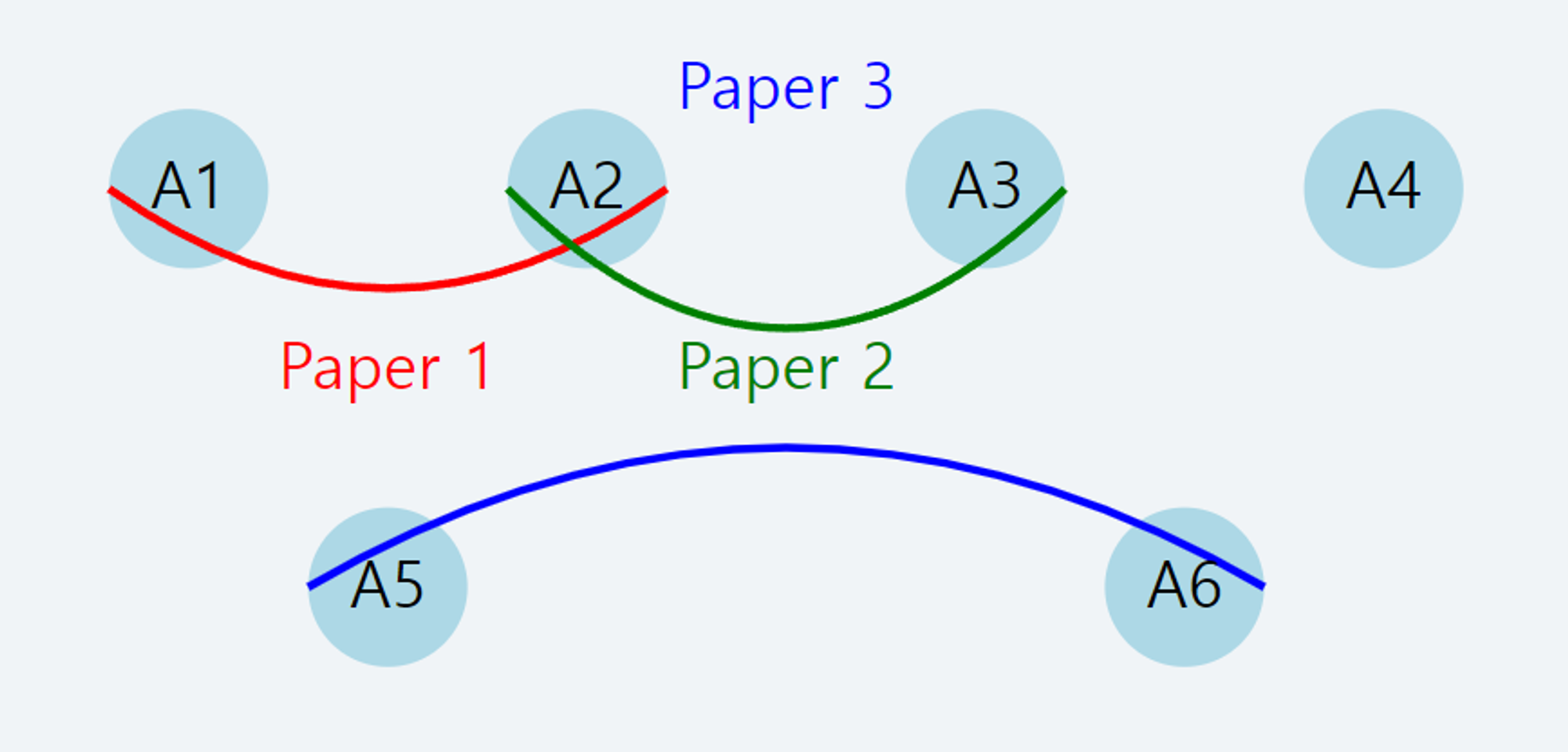
- 실생활 예시: 학술 논문 공저자 관계
  - 노드: 연구자들
  - 하이퍼엣지: 하나의 논문 (여러 저자를 동시에 연결)
동적 그래프(Dynamic Graphs):
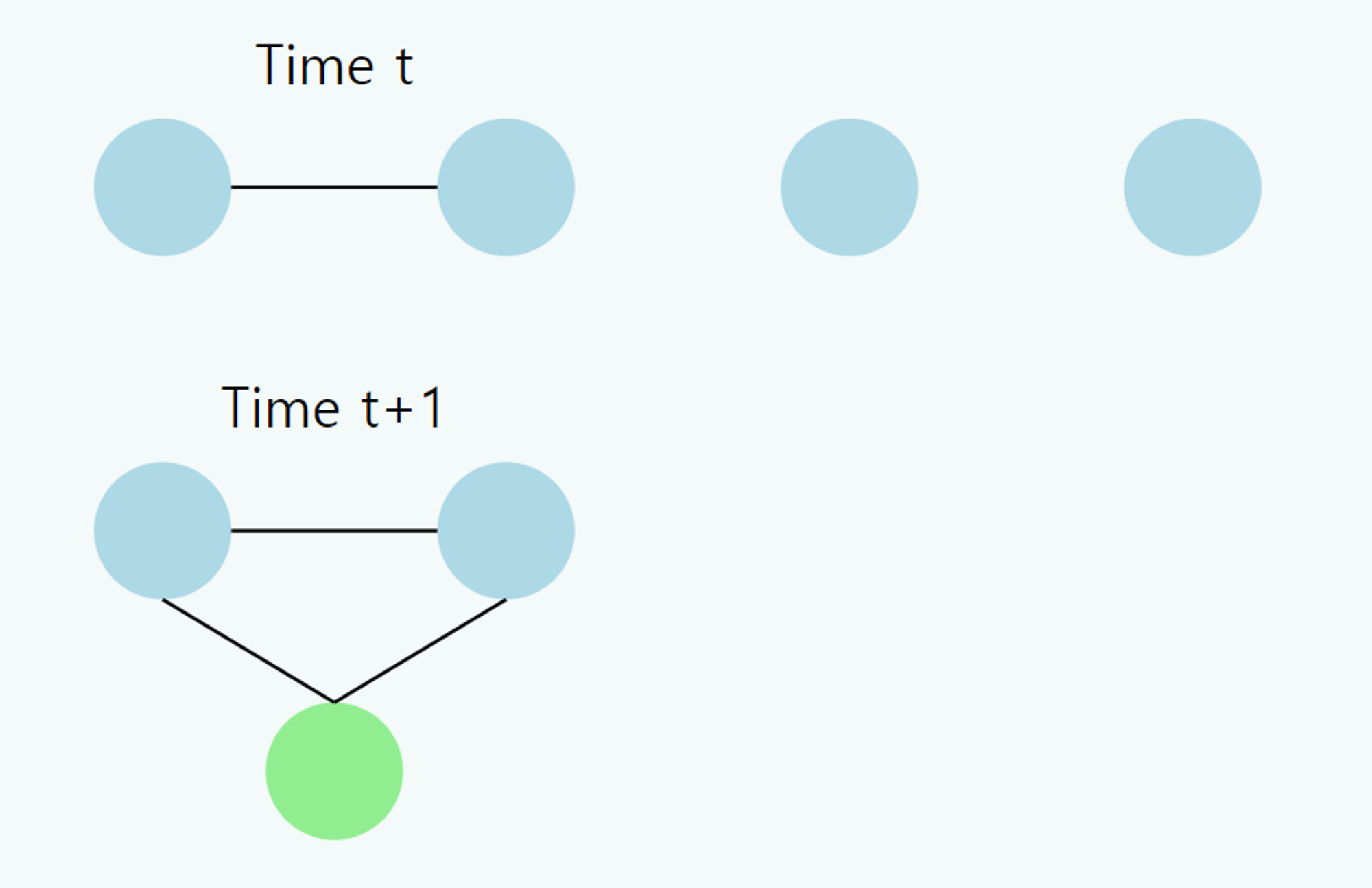
- 개념: 시간에 따라 구조가 변하는 그래프입니다.
- 특징:
  - 노드와 엣지가 시간에 따라 추가되거나 제거될 수 있습니다.
  - 시간에 따른 네트워크의 진화를 모델링할 수 있습니다.
- 실생활 예시: 시간에 따른 소셜 네트워크의 변화
  - 노드: 사용자
  - 엣지: 친구 관계
  - 시간에 따라 새로운 사용자 가입, 친구 관계 형성 또는 해제

7. 그래프로 무엇을 계산할 수 있는가? (What we can compute with graphs?)

노드 중심 작업 (Node-focused tasks):
- 노드 분류 (Node Classification): 각 노드에 레이블을 할당하는 작업입니다.
  - 예시: 소셜 네트워크에서 사용자 프로필을 분석하여 각 사용자의 관심사를 분류할 수 있습니다.
- 링크 예측 (Link Prediction): 두 노드 간의 에지가 존재할 가능성을 예측하는 작업입니다.
  - 예시: 친구 추천 시스템에서 사용자가 새롭게 친구가 될 가능성이 높은 사용자를 예측할 수 있습니다.
그래프 중심 작업 (Graph-focused tasks):
- 그래프 분류 (Graph Classification): 그래프 전체에 레이블을 할당하는 작업입니다.
  - 예시: 화학 구조 그래프를 분석하여 특정 분자가 약물로 사용될 수 있는지 분류할 수 있습니다.

요약

위 내용을 통해 그래프 이론의 기본 개념과 다양한 중심성 지표, 그래프 신호 처리, 복잡한 그래프의 유형, 그리고 그래프를 사용하여 수행할 수 있는 다양한 작업에 대해 자세히 이해할 수 있습니다.
이러한 기초 지식을 바탕으로 그래프 신경망(GNN)을 구축하고 다양한 데이터 과학 문제에 적용할 수 있습니다.