[개념정리] 시계열 인과관계 분석: Granger Causality
안녕하세요😊 지난 번 포스트에서 “인과관계와 상관관계의 개념”(링크)에 대해서 살펴보았는데요.
오늘은 시계열 분석의 핵심 개념 중 하나인 ‘그랜저 인과관계(Granger causality)’에 대해 알아보고, 이를 실제 데이터에 적용해보는 시간을 가져보겠습니다.
실습에 사용할 데이터는 Kaggle 데이터 중 하나인 Advertising Sales Dataset(링크)로, 해당 데이터를 통해 광고 예산이 매출에 어떤 영향을 미치는지 확인해보실 수 있을 겁니다⭐
-
인과관계 vs 상관관계
먼저 복습 차원에서 간단하게 인과관계와 상관관계의 차이부터 알아봅시다.
인과관계 (Causal Relationship)
정의: 한 사건이 다른 사건을 직접적으로 야기하는 관계예: 흡연이 폐암 발병률을 증가시킴
상관관계 (Correlation)
정의: 두 변수 간의 선형적 관련성의 정도예: 아이스크림 판매량과 범죄율이 함께 증가하는 경향 (실제 원인은 더운 날씨일 수 있음)
차이점
방향성: 인과관계는 방향이 있지만, 상관관계는 방향성이 없습니다.원인과 결과: 인과관계는 원인과 결과를 명확히 구분하지만, 상관관계는 그렇지 않습니다.
-
그랜저 인과관계
그랜저 인과관계(Granger causality)는 1969년 클라이브 그랜저가 제안한 개념으로, 시계열 데이터에서의 예측 가능성을 기반으로 한 인과관계를 의미합니다.
그랜저 인과관계의 정의
(Def) X의 과거 정보가 Y의 미래 값을 예측하는 데 통계적으로 유의미한 도움을 준다면, “X는 Y를 그랜저 인과한다”고 말합니다.
💯 이는 수학적으로 다음과 같이 표현할 수 있습니다:
| P(Y(t+1)∣Y(t),Y(t−1),…,X(t),X(t−1),…)≠P(Y(t+1)∣Y(t),Y(t−1),…)P(Y(t+1) | Y(t), Y(t-1), …, X(t), X(t-1), …) ≠ P(Y(t+1) | Y(t), Y(t-1), …)P(Y(t+1)∣Y(t),Y(t−1),…,X(t),X(t−1),…)=P(Y(t+1)∣Y(t),Y(t−1),…) |
이때 PPP는 조건부 확률을 나타냅니다.
-
좌변 P(Y(t+1) Y(t), Y(t-1), ...,X(t), X(t-1), ...):- Y의 미래 값 Y(t+1)을 예측할 때,
Y의 과거 값들(Y(t), Y(t-1), ...)과X의 과거 값들(X(t), X(t-1), ...)을 모두 사용한 조건부 확률을 나타냅니다.
- Y의 미래 값 Y(t+1)을 예측할 때,
-
우변 P(Y(t+1) Y(t), Y(t-1), ...):- Y의 미래 값 Y(t+1)을 예측할 때,
Y의 과거 값들(Y(t), Y(t-1), ...)만을 사용한 조건부 확률을 나타냅니다.
- Y의 미래 값 Y(t+1)을 예측할 때,
-
부등호 (≠):
- 두 조건부 확률이 서로 다르다는 것을 의미합니다.
💡 위 수식의 의미:
- 만약 X가 Y를 그랜저 인과한다면, X의 과거 값들을 포함하여 예측한 Y의 미래 값(좌변)이 Y의 과거 값들만으로 예측한 경우(우변)와 다를 것입니다.
- 즉, X의 정보가 Y의 예측에 유의미한 영향을 준다는 것을 나타냅니다.
💡 실제 적용:
- 이 개념을 통계적으로 검정하기 위해, 보통 선형 회귀 모델을 사용하여 두 경우(X 포함 vs X 미포함)의 예측 오차를 비교합니다.
- F-검정이나 다른 통계적 방법을 사용하여 두 모델 간의 차이가 유의미한지 판단합니다.
⚠️ 주의점:
- 이는 예측 가능성에 기반한 인과관계이며, 진정한 인과관계를 완벽히 증명하지는 않습니다.
- 숨겨진 변수나 공통 원인 등의 가능성을 항상 고려해야 합니다.
이처럼 위 수식은 그랜저 인과관계의 기본 아이디어를 간결하게 표현하고 있으며, 시계열 데이터 분석에서 변수 간의 관계를 이해하는 데 중요한 도구로 사용됩니다.
-
그랜저 인과관계 vs 인과관계
그랜저 인과관계와 일반적인 인과관계는 다음과 같은 차이가 존재합니다:
-
정의:
- 인과관계: A가 B의
직접적인 원인이 됨 - 그랜저 인과관계: A의 과거 정보가 B의 미래를 예측하는 데 도움이 됨
- 인과관계: A가 B의
-
기반:
- 인과관계: 논리적, 실험적 증거에 기반
- 그랜저 인과관계: 통계적 예측력에 기반
-
해석:
- 인과관계: “A가 B를 야기한다”
- 그랜저 인과관계: “A가 B를 예측하는 데 도움이 된다”
-
그랜저 인과관계 모형
모형의 전제
시간 선후관계: 과거의 사건은 현재의 사건을 유발할 수 있지만, 미래의 사건은 현재의 사건을 유발할 수 없습니다.정상성: 데이터는 정상성(stationary)을 가져야 합니다. 즉, 평균과 분산이 시간에 따라 일정해야 합니다.입력시차: 예상되는 시차만큼의 과거 데이터를 모두 입력변수로 사용해야 합니다.최종시차: 적절한 시차를 선택해야 합니다. 보통 연 환산 빈도의 2~3배까지 고려합니다.
모형의 검정
그랜저 인과관계 검정은 다음과 같은 단계로 이루어집니다:
- 귀무가설 설정: “X는 Y를 그랜저 인과하지 않는다”
- 제한 모델과 비제한 모델 구축:
- 제한 모델: Y(t) = α + β1Y(t-1) + β2Y(t-2) + … + βp*Y(t-p) + ε
- 비제한 모델: Y(t) = α + β1Y(t-1) + … + βpY(t-p) + γ1X(t-1) + … + γpX(t-p) + ε
- F-통계량 계산
- p-value 확인 및 결론 도출
파이썬 코드 예시
statsmodels 라이브러리를 사용하여 그랜저 인과관계 검정을 수행할 수 있습니다:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import numpy as np
import pandas as pd
from statsmodels.tsa.stattools import grangercausalitytests
# 예시 데이터 생성
np.random.seed(1)
x = np.random.randn(1000)
y = np.random.randn(1000)
y[1:] += 0.5 * x[:-1] # X가 Y를 그랜저 인과하도록 설정
data = pd.DataFrame({'X': x, 'Y': y})
# 그랜저 인과관계 검정
result = grangercausalitytests(data[['Y', 'X']], maxlag=5)
# 결과 출력
for lag, values in result.items():
print(f"Lag {lag}:")
print(f" F-statistic: {values[0]['ssr_ftest'][0]}")
print(f" p-value: {values[0]['ssr_ftest'][1]}")
-
모형의 응용
VAR을 활용한 응용
VAR이란?
- VAR(Vector Autoregression)은
여러 변수의 시계열 데이터를 동시에 모델링하는 방법입니다. - 각 변수가 자신의 과거 값과 다른 변수들의 과거 값에 의해 영향을 받는다고 가정합니다.
VAR(p) 모델 (p차 벡터 자기회귀 모델):
Yt=c+A1Yt−1+A2Yt−2+…+ApYt−p+ϵtY_t = c + A_1Y_{t-1} + A_2Y_{t-2} + … + A_pY_{t-p} + \epsilon_tYt=c+A1Yt−1+A2Yt−2+…+ApYt−p+ϵt
여기서:
- YtY_tYt 는 시점 t에서의 k차원 시계열 벡터
- ccc 는 k차원 상수 벡터
- AiA_iAi 는 k × k 계수 행렬
- ϵt\epsilon_tϵt 는 k차원 백색 잡음 벡터
VAR을 어떻게 활용해서 응용하는가?
- 변수 간 동적 관계 분석: VAR 모델은 여러 변수 간의 상호작용을 동시에 고려할 수 있습니다.
- 충격반응함수 분석: 한 변수의 변화가 다른 변수에 미치는 영향을 시간에 따라 추적할 수 있습니다.
- 예측: 여러 변수의 미래 값을 동시에 예측할 수 있습니다.
파이썬 코드 예시:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from statsmodels.tsa.api import VAR
from statsmodels.tsa.stattools import adfuller
# 데이터 정상화 (필요한 경우)
def difference(data):
return data.diff().dropna()
# ADF 테스트로 정상성 확인
def adf_test(series):
result = adfuller(series)
print(f'ADF Statistic: {result[0]}')
print(f'p-value: {result[1]}')
# VAR 모델 적용
model = VAR(data)
results = model.fit(maxlags=15, ic='aic')
# 그랜저 인과관계 검정
granger_results = results.test_causality('Y', 'X', kind='f')
print(granger_results.summary())
ARIMA를 활용한 응용
ARIMA란?
- ARIMA(AutoRegressive Integrated Moving Average)는
단일 시계열 데이터를 모델링하는 방법입니다. - 자기회귀(AR), 차분(I), 이동평균(MA) 요소를 결합하여 복잡한 시계열 패턴을 포착합니다.
ARIMA(p,d,q) 모델:
ϕ(B)(1−B)dXt=θ(B)ϵt\phi(B)(1-B)^d X_t = \theta(B)\epsilon_tϕ(B)(1−B)dXt=θ(B)ϵt
여기서:
- BBB 는 후행 연산자 (BXt=Xt−1BX_t = X_{t-1}BXt=Xt−1)
- ddd 는 차분 차수
- ϕ(B)=1−ϕ1B−ϕ2B2−…−ϕpBp\phi(B) = 1 - \phi_1B - \phi_2B^2 - … - \phi_pB^pϕ(B)=1−ϕ1B−ϕ2B2−…−ϕpBp (AR 다항식)
- θ(B)=1+θ1B+θ2B2+…+θqBq\theta(B) = 1 + \theta_1B + \theta_2B^2 + … + \theta_qB^qθ(B)=1+θ1B+θ2B2+…+θqBq (MA 다항식)
- ϵt\epsilon_tϵt 는 백색 잡음 과정
ARIMA를 어떻게 활용해서 응용하는가?
- 단변량 시계열 분석: 각 변수의 자체적인 시계열 특성을 자세히 분석할 수 있습니다.
- 예측: 단일 변수의 미래 값을 예측할 수 있습니다.
- 이상치 탐지: 모델의 예측값과 실제값의 차이를 통해 이상치를 탐지할 수 있습니다.
파이썬 코드 예시:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from statsmodels.tsa.arima.model import ARIMA
import matplotlib.pyplot as plt
# ARIMA 모델 적용
model = ARIMA(data['Y'], order=(1,1,1))
results = model.fit()
# 예측
forecast = results.forecast(steps=10)
# 결과 시각화
plt.figure(figsize=(12,6))
plt.plot(data['Y'], label='Observed')
plt.plot(forecast, label='Forecast')
plt.legend()
plt.show()
모형의 해석
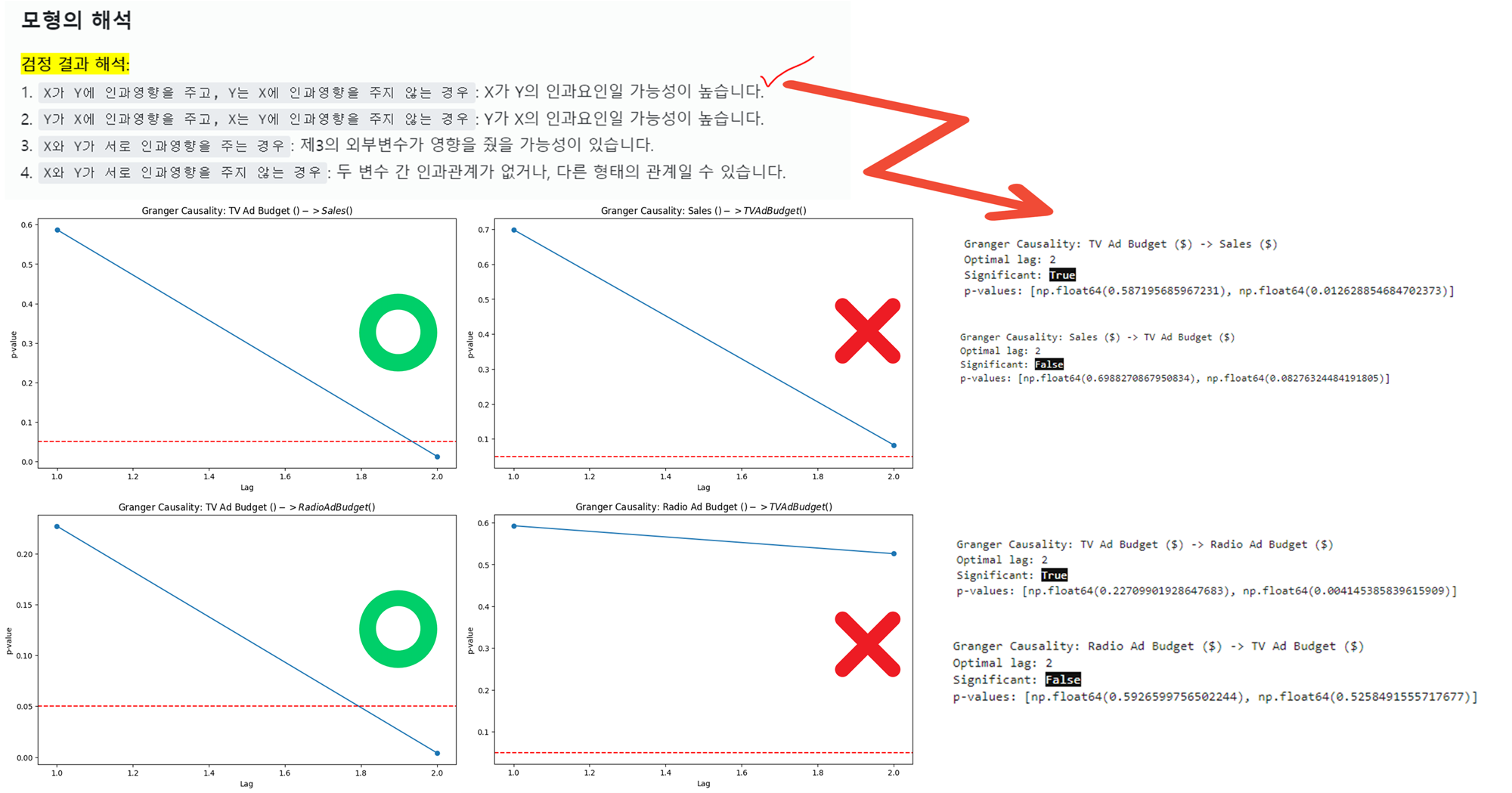
검정 결과 해석:
X가 Y에 인과영향을 주고, Y는 X에 인과영향을 주지 않는 경우: X가 Y의 인과요인일 가능성이 높습니다.Y가 X에 인과영향을 주고, X는 Y에 인과영향을 주지 않는 경우: Y가 X의 인과요인일 가능성이 높습니다.X와 Y가 서로 인과영향을 주는 경우: 제3의 외부변수가 영향을 줬을 가능성이 있습니다.-
X와 Y가 서로 인과영향을 주지 않는 경우: 두 변수 간 인과관계가 없거나, 다른 형태의 관계일 수 있습니다. -
실제 데이터 분석예제
이제 실제 데이터를 사용하여 그랜저 인과관계, VAR, ARIMA 모델을 적용해보겠습니다.
데이터 소개
우리가 사용할 데이터셋은 TV, 라디오, 신문 광고 예산과 그에 따른 매출 데이터를 포함하고 있습니다. 총 200개의 관측치가 있으며, 각 관측치는 다음 변수들로 구성되어 있습니다:
- TV Ad Budget ($): TV 광고 예산
- Radio Ad Budget ($): 라디오 광고 예산
- Newspaper Ad Budget ($): 신문 광고 예산
- Sales ($): 매출
데이터 준비 및 분석
먼저, 필요한 라이브러리를 임포트하고 데이터를 로드합니다.
필요 라이브러리 로드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 필요 라이브러리 로드
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
from statsmodels.tsa.api import VAR
import statsmodels.tsa.api as smt
from statsmodels.tsa.stattools import grangercausalitytests
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.arima.model import ARIMA
데이터 로드
1
2
3
4
5
6
# 데이터 로드 (데이터는 직접 다운 받아주세요)
# https://www.kaggle.com/datasets/yasserh/advertising-sales-dataset
df = pd.read_csv("./Data/Advertising Budget and Sales.csv")
print(df.shape)
df.head()
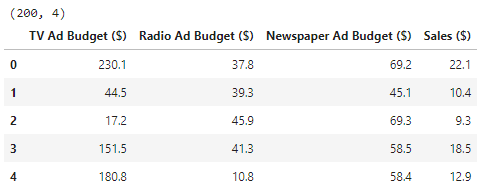
정규화 및 시각화
1
2
3
4
5
6
7
variables = ['TV Ad Budget ($)', 'Radio Ad Budget ($)', 'Newspaper Ad Budget ($)', 'Sales ($)']
# 각 값의 첫 값으로 정규화
df['Sales ($)'] = df['Sales ($)'] / df['Sales ($)'].iloc[0]
df['TV Ad Budget ($)'] = df['TV Ad Budget ($)'] / df['TV Ad Budget ($)'].iloc[0]
df['Radio Ad Budget ($)'] = df['Radio Ad Budget ($)'] / df['Radio Ad Budget ($)'].iloc[0]
df['Newspaper Ad Budget ($)'] = df['Newspaper Ad Budget ($)'] / df['Newspaper Ad Budget ($)'].iloc[0]
❓ 어? 제가 아는 정규화랑 조금 다른데요? => 맞습니다
- 이는
상대적 변화 정규화(또는 기준점 정규화)라고 불리며, 일반적인 정규화 방법과는 다른 목적과 특징을 가지고 있습니다.- 이 방법의 주요 특징과 일반 정규화와의 차이점을 설명드리겠습니다:
🔶 상대적 변화 정규화의 목적
시계열 데이터 분석: 시간에 따른 변화를 더 쉽게 파악할 수 있게 합니다. 초기 값 대비 증가 또는 감소를 직관적으로 이해할 수 있습니다.변수 간 상대적 변화 비교: 서로 다른 단위나 스케일을 가진 변수들의 변화를 비교하기 쉽게 만듭니다.그랜저 인과성 분석에 유용: 변수들 간의 상대적인 변화를 비교하기 쉽게 만들어 인과관계 분석에 도움을 줍니다.
🔷 일반 정규화와의 차이점
데이터 변환 관점:
- 상대적 변화 정규화: 첫 번째 값을 기준으로 모든 값을 나눕니다.
- 일반 정규화(예: Min-Max): 전체 데이터 범위를 특정 범위(예: 0-1)로 변환합니다.
결과 해석 관점:
- 상대적 변화 정규화: 초기 값 대비 변화율을 나타냅니다.
- 일반 정규화: 전체 데이터 범위 내에서의 상대적 위치를 나타냅니다.
데이터 분포 관점:
- 상대적 변화 정규화: 원래 데이터의 상대적 변화 패턴을 유지합니다.
- 일반 정규화: 데이터의 전체적인 분포를 변경할 수 있습니다.
1
2
df.plot(figsize=(15,3))
plt.show()
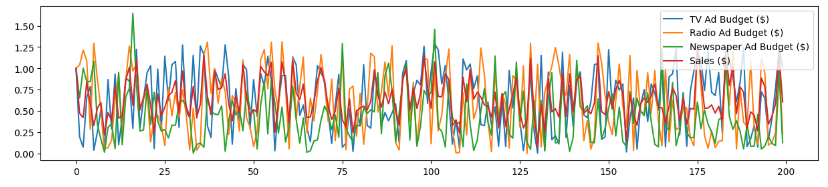
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# matplotlib의 기본 색상 순서 사용
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
# 각 변수를 별도의 서브플롯으로 그리기
fig, axes = plt.subplots(len(variables), 1, figsize=(15, 3*len(variables)))
fig.suptitle('Normalized Values Over Time (Subplots)', fontsize=16)
for i, var in enumerate(variables):
axes[i].plot(df.index, df[var], label=var, color=colors[i])
axes[i].set_title(var)
axes[i].set_xlabel('Index')
axes[i].set_ylabel('Normalized Value')
axes[i].legend()
axes[i].grid(True)
# y축 범위 설정 (0부터 데이터의 최대값까지)
axes[i].set_ylim(0, df[var].max() * 1.1) # 최대값에 10% 여유 추가
plt.tight_layout()
plt.show()
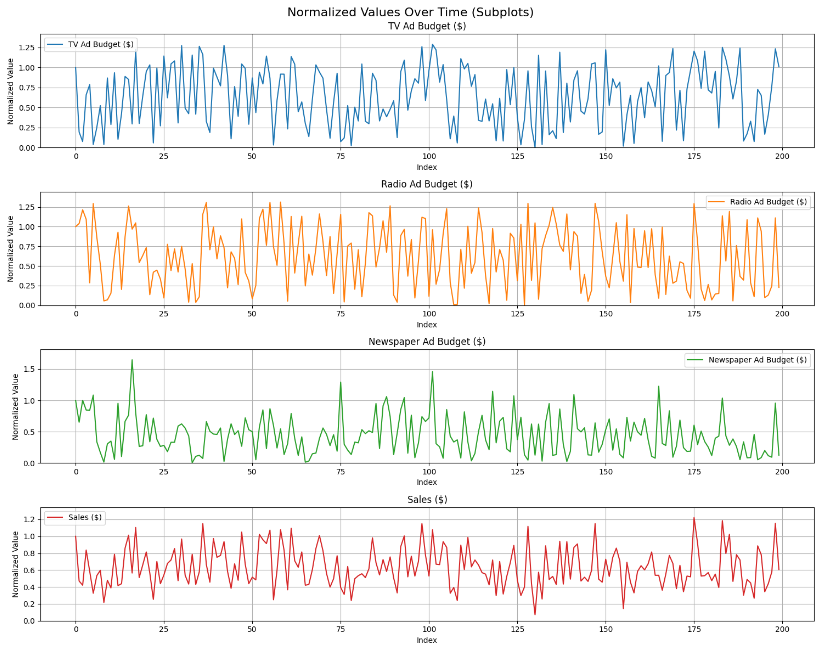
정상성 확인
본격적으로 그랜저 인과관계 검정을 수행하기에 앞서 데이터가 정상성(stationary)을 가지는지 확인을 해야합니다. 그렇지 않다면 별도로 차분을 수행해주어야 합니다.
(앞에 개념 내용 참고)
- 정상성: 데이터는 정상성(stationary)을 가져야 합니다. 즉, 평균과 분산이 시간에 따라 일정해야 합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from statsmodels.tsa.stattools import adfuller, grangercausalitytests
# ADF 테스트 함수 정의
def adf_test(timeseries):
result = adfuller(timeseries, autolag='AIC')
return pd.Series({'Test Statistic': result[0], 'p-value': result[1], 'Critical Values': result[4]})
adf_results = {var: adf_test(df[var]) for var in variables}
# ADF 테스트 결과 출력 및 해석
for var, result in adf_results.items():
print(f"\nADF Test Results for {var}:")
print(result)
if result['p-value'] <= 0.05:
print(f"해석: {var}는 5% 유의수준에서 정상 시계열입니다.")
else:
print(f"해석: {var}는 5% 유의수준에서 비정상 시계열입니다.")
아래 ADF 테스트 결과를 보면, 모든 변수들이 5% 유의수준에서 정상 시계열로 나타났습니다. 이는 그랜저 인과관계 분석을 위해 별도의 차분이 필요하지 않다는 것을 의미합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 결과
ADF Test Results for TV Ad Budget ($):
Test Statistic -14.158141
p-value 0.0
Critical Values {'1%': -3.4636447617687436, '5%': -2.876176117...
dtype: object
해석: TV Ad Budget ($)는 5% 유의수준에서 정상 시계열입니다.
ADF Test Results for Radio Ad Budget ($):
Test Statistic -14.129897
p-value 0.0
Critical Values {'1%': -3.4636447617687436, '5%': -2.876176117...
dtype: object
해석: Radio Ad Budget ($)는 5% 유의수준에서 정상 시계열입니다.
ADF Test Results for Newspaper Ad Budget ($):
Test Statistic -13.344195
p-value 0.0
Critical Values {'1%': -3.4636447617687436, '5%': -2.876176117...
dtype: object
해석: Newspaper Ad Budget ($)는 5% 유의수준에서 정상 시계열입니다.
ADF Test Results for Sales ($):
Test Statistic -13.990162
p-value 0.0
Critical Values {'1%': -3.4636447617687436, '5%': -2.876176117...
dtype: object
해석: Sales ($)는 5% 유의수준에서 정상 시계열입니다.
그랜저 인과관계 검정
그렇다면 이제 그랜저 인과관계 검정을 통해 각 광고 채널의 예산이 매출에 영향을 미치는지 확인해보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import grangercausalitytests
from statsmodels.tsa.api import VAR
from statsmodels.tools.eval_measures import aic, bic
def optimal_lag(data, max_lag):
model = VAR(data)
results = {}
for lag in range(1, max_lag + 1):
result = model.fit(lag)
results[lag] = result.aic
return min(results, key=results.get)
def granger_causality(data, variables, max_lag=12, alpha=0.05):
results = {}
for i in range(len(variables)):
for j in range(len(variables)):
if i != j:
pair = (variables[i], variables[j])
opt_lag = optimal_lag(data[[variables[i], variables[j]]], max_lag)
granger_result = grangercausalitytests(data[[variables[i], variables[j]]], maxlag=opt_lag, verbose=False)
p_values = [granger_result[lag][0]['ssr_ftest'][1] for lag in range(1, opt_lag+1)]
results[pair] = {
'optimal_lag': opt_lag,
'p_values': p_values,
'significant': any(p < alpha for p in p_values)
}
plt.figure(figsize=(10, 6))
plt.plot(range(1, opt_lag+1), p_values, marker='o')
plt.axhline(y=alpha, color='r', linestyle='--')
plt.title(f'Granger Causality: {variables[i]} -> {variables[j]}')
plt.xlabel('Lag')
plt.ylabel('p-value')
plt.show()
return results
# 그랜저 인과관계 분석 수행
results = granger_causality(df, variables)
# 결과 출력
for pair, result in results.items():
print(f"\nGranger Causality: {pair[0]} -> {pair[1]}")
print(f"Optimal lag: {result['optimal_lag']}")
print(f"Significant: {result['significant']}")
print(f"p-values: {result['p_values']}")
결과해석
- 유의미한 그랜저 인과관계:
- TV Ad Budget(X) -> Radio Ad Budget (Y):
2 lag에서 유의미함. - TV Ad Budget(X) -> Sales (Y):
2 lag에서 유의미함.
- 다른 관계들:
- 대부분의 관계가 통계적으로 무의미함.
- 주요 인사이트:
TV 광고 예산이라디오 광고 예산과매출에 영향을 미치는 것으로 보임.
이제 이를 활용해서 Sales Forecasting을 구축해보겠습니다.
- VAR 모델(또는 ARIMA 모델) 사용:
- TV Ad Budget과 Sales를 포함한 VAR 모델(또는 ARIMA 모델) 구축
- 최적 lag는 2로 설정
- 특성 선택:
- TV Ad Budget(X)을 독립변수, Sales(Y)를 종속변수로 모델링해보겠습니다.
Train/Test Split
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.api import VAR
from statsmodels.tsa.arima.model import ARIMA
from sklearn.metrics import mean_squared_error
from math import sqrt
# 데이터 로드
df = pd.read_csv("./Data/Advertising Budget and Sales.csv")
df = df[['TV Ad Budget ($)', 'Sales ($)']]
df['Sales ($)'] = df['Sales ($)'] / df['Sales ($)'].iloc[0]
df['TV Ad Budget ($)'] = df['TV Ad Budget ($)'] / df['TV Ad Budget ($)'].iloc[0]
df.columns = ['tv', 'sales'] # 간단하게 이름 변경
# 데이터 분할 (80% 훈련, 20% 테스트)
train_size = int(len(df) * 0.8)
train, test = df[:train_size], df[train_size:]
# 그래프 설정
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10), sharex=True)
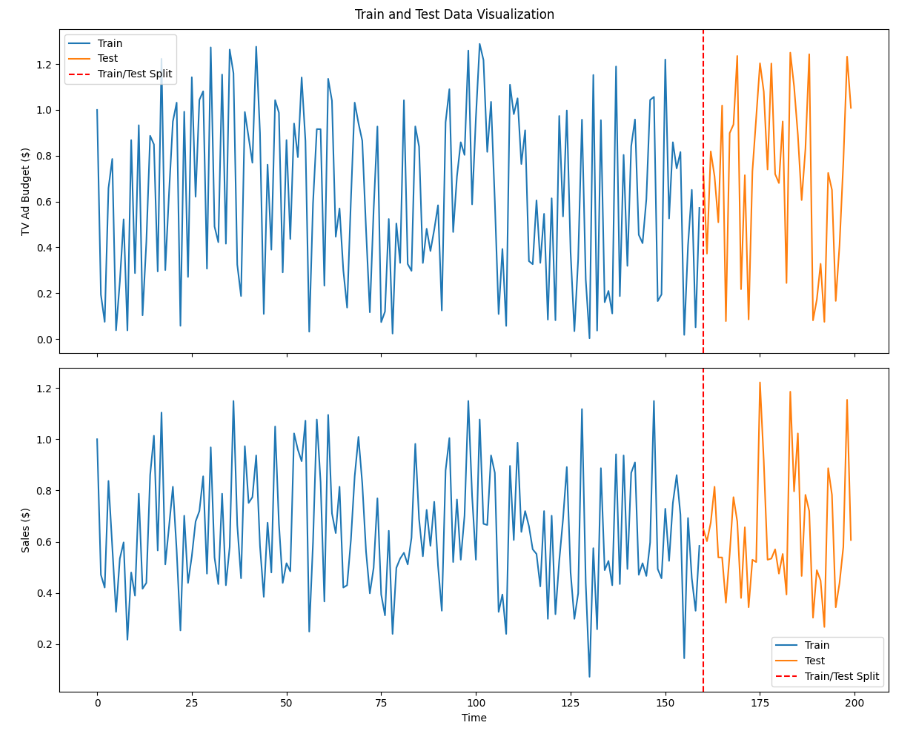
fig.suptitle('Train and Test Data Visualization')
# TV Ad Budget 그래프
ax1.plot(df.index[:train_size], train['tv'], label='Train')
ax1.plot(df.index[train_size:], test['tv'], label='Test')
ax1.axvline(x=train_size, color='r', linestyle='--', label='Train/Test Split')
ax1.set_ylabel('TV Ad Budget ($)')
ax1.legend()
# Sales 그래프
ax2.plot(df.index[:train_size], train['sales'], label='Train')
ax2.plot(df.index[train_size:], test['sales'], label='Test')
ax2.axvline(x=train_size, color='r', linestyle='--', label='Train/Test Split')
ax2.set_ylabel('Sales ($)')
ax2.legend()
# x축 레이블 설정
ax2.set_xlabel('Time')
plt.tight_layout()
plt.show()
VAR (Vector Autoregression) 모델
이제 VAR 모델을 사용하여 변수들 간의 동적 관계를 분석해보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# USING VAR
lag = 2
# VAR 모델
model_var = VAR(train)
results_var = model_var.fit(lag)
# VAR 동적 예측
forecast_var = []
forecast_input_var = train.values[-lag:]
for i in range(len(test)):
fc = results_var.forecast(forecast_input_var, steps=1)
forecast_var.append(fc[0])
# 실제 test 데이터의 이전 lag 값으로 forecast_input_var 업데이트
if i + 1 < len(test):
forecast_input_var = np.vstack([forecast_input_var[1:], test.iloc[i].values])
forecast_var = np.array(forecast_var)
rmse_var_sales = sqrt(mean_squared_error(test['sales'], forecast_var[:, 1]))
비교를 위해 SALES만 가지고 학습을 한 ARIMA 모델을 학습시켜보겠습니다!
ARIMA (AutoRegressive Integrated Moving Average) 모델
마지막으로, 매출 데이터에 대해 ARIMA 모델을 적용해보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
train_sales = train['sales']
test_sales = test['sales']
# ARIMA 모델
model_arima = ARIMA(train_sales, order=(lag, 0, 0))
results_arima = model_arima.fit()
# 동적 예측을 위한 ARIMA
forecast_arima_dynamic = []
history = train_sales.tolist()
for t in range(len(test_sales)):
model_arima_dynamic = ARIMA(history, order=(lag, 0, 0))
model_fit_dynamic = model_arima_dynamic.fit()
yhat = model_fit_dynamic.forecast(steps=1)[0]
forecast_arima_dynamic.append(yhat)
history.append(test_sales.iloc[t])
rmse_arima_sales_dynamic = sqrt(mean_squared_error(test_sales, forecast_arima_dynamic))
모델 비교
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
print("\nModel Comparison:")
print(f"VAR Model RMSE: {rmse_var_sales:.5f}")
print(f"VAR Model MSE: {mse_var_sales:.5f}")
print(f"VAR Model MAE: {mae_var_sales:.5f}")
print("-"*50)
print(f"ARIMA Model RMSE: {rmse_arima_sales_dynamic:.5f}")
print(f"ARIMA Model MSE: {mse_arima_sales_dynamic:.5f}")
print(f"ARIMA Model MAE: {mae_arima_sales_dynamic:.5f}")
# Model Comparison:
# VAR Model RMSE: 0.23431
# VAR Model MSE: 0.05490
# VAR Model MAE: 0.19481
# --------------------------------------------------
# ARIMA Model RMSE: 0.23493
# ARIMA Model MSE: 0.05519
# ARIMA Model MAE: 0.18524
1
2
3
4
5
6
7
8
9
10
11
12
# 예측 결과 시각화
plt.figure(figsize=(12, 6))
plt.plot(test.index, test.sales, label='Actual Sales', color='black')
plt.plot(test.index, test.tv, label='Actual TV', color='orange', linestyle = '--')
plt.plot(test.index, forecast_var[:, 1], label='VAR Sales Forecast', color='blue')
plt.plot(test.index, forecast_arima_dynamic, label='Dynamic ARIMA Sales Forecast', color='red')
plt.legend()
plt.xlabel('Time')
plt.ylabel('Sales ($)')
plt.title('Sales Forecast Comparison: VAR vs Dynamic ARIMA')
plt.show()
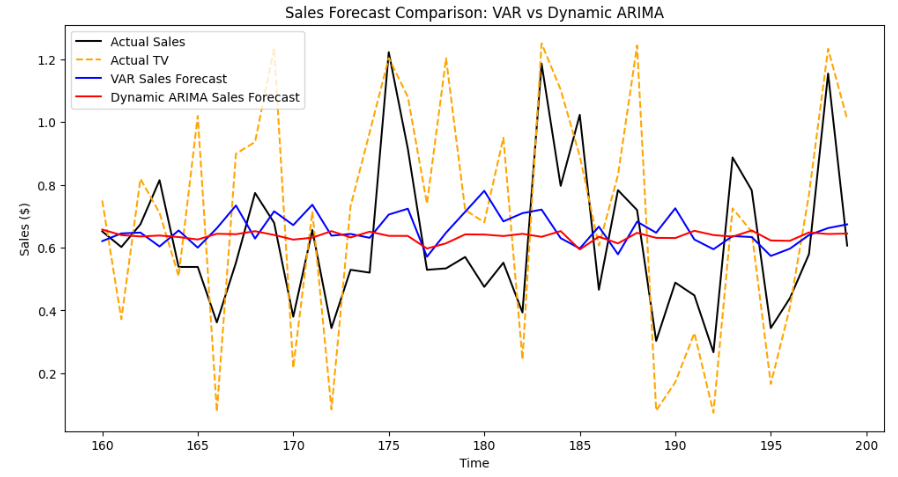
분석 해석
제공된 성능 지표와 시각적 검토를 종합해 볼 때, 특별히 어느 한 모델이 더 우수하다고 결론 내리기는 어렵습니다. 두 모델 모두 비슷한 수준의 예측 성능을 보이기 때문에, 최종 모델 선택은 다음과 같은 추가적인 요소를 고려해야 합니다:
모델 해석성: TV Ad Budget 변수가 Sales에 중요한 영향을 미친다고 판단된다면 VAR 모델이 더 적합할 수 있습니다.모델의 목적: 예측의 목적이 무엇인지에 따라 모델을 선택할 수 있습니다. 예를 들어, 단순히 과거 Sales 데이터를 기반으로 예측하고자 한다면 동적 ARIMA 모델이 더 적합할 수 있습니다.복잡도: VAR 모델은 다변량 시계열 데이터를 다루기 때문에 모델이 더 복잡할 수 있으며, 동적 ARIMA 모델은 단변량 시계열 데이터를 다루기 때문에 상대적으로 단순할 수 있습니다.데이터 가용성: 추가적인 외생 변수가 있을 경우 VAR 모델이 유리할 수 있습니다.
따라서, 실제 사용 목적과 상황에 맞추어 두 모델 중 적합한 것을 선택하는 것이 바람직합니다.
그랜저 인과관계, VAR, ARIMA 모델은 각각 장단점이 있으며, 데이터의 특성과 분석 목적에 따라 적절한 모델을 선택하는 것이 중요합니다. 이러한 기법들을 잘 활용한다면, 데이터에 숨겨진 인사이트를 발견하고 더 나은 비즈니스 의사결정을 내릴 수 있을 것입니다.
오늘도 도움이 되셨길 바라며 저도 이만 프로젝트에 적용하러 가보겠습니다! ⭐