[개념] Deep Learning Normalization Techniques

원본 게시글: https://velog.io/@euisuk-chung/개념정리-Deep-Learning-Normalization

딥러닝에서의 정규화 기법

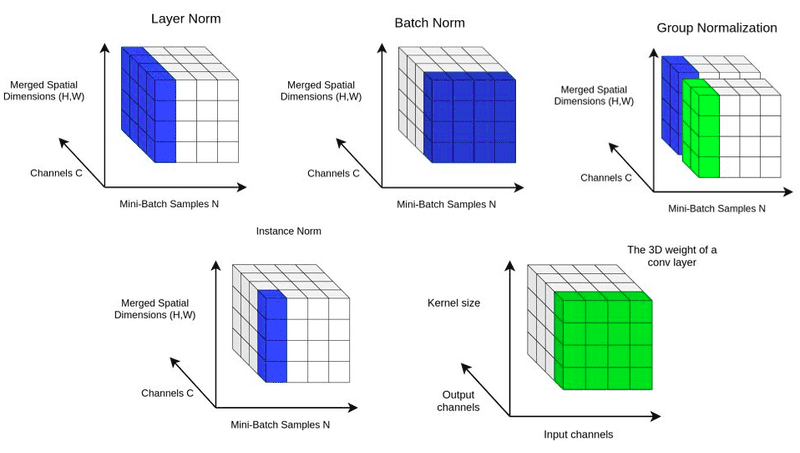
출처: https://theaisummer.com/normalization/

정규화의 정의와 목적

정규화(Normalization)는 데이터의 스케일을 조정하는 과정으로, 머신러닝과 딥러닝에서 모두 중요한 역할을 합니다. 그러나 전통적인 머신러닝에서의 정규화와 딥러닝에서의 정규화는 그 목적과 방법에 있어 약간의 차이가 있습니다.

머신러닝에서의 정규화

전통적인 머신러닝에서 정규화의 주요 목적은 다음과 같습니다:

특성 간 단위 차이 해소: 서로 다른 단위나 범위를 가진 특성들을 동일한 스케일로 조정합니다.
모델의 안정성 향상: 특성 간 스케일 차이로 인한 학습의 불안정성을 줄입니다.
학습 속도 개선: 경사 하강법 등의 최적화 알고리즘의 수렴 속도를 높입니다.

주로 사용되는 방법:

Min-Max Scaling: 데이터를 [0, 1] 범위로 스케일링
tandardization : 평균을 0, 표준편차를 1로 조정

딥러닝에서의 정규화

딥러닝에서의 정규화는 위의 목적들을 포함하면서도, 다음과 같은 추가적인 목적을 가집니다:

내부 공변량 변화 감소: 네트워크의 각 층에서 입력 분포의 변화를 줄입니다.

내부 공변량 변화(Internal Coveriate Shift)란?

✍️Internal Covariate Shift는 네트워크의 각 Layer나 Activation마다 출력값의 데이터 분포가 Layer마다 다르게 나타나는 현상을 말한다.
기울기 소실/폭발 문제 완화: 깊은 네트워크에서 발생하는 기울기 소실 또는 폭발 문제를 완화합니다.
일반화 성능 향상: 과적합을 줄이고 모델의 일반화 능력을 향상시킵니다.
학습 안정성 제공: 높은 학습률 사용을 가능하게 하여 학습을 가속화합니다.

주요 차이점

적용 시점:
- 전통적 ML: 주로 전처리 단계에서 데이터셋 전체에 적용
- 딥러닝: 네트워크의 각 층에서 동적으로 적용
적용 범위:
- 전통적 ML: 주로 입력 특성에 대해 적용
- 딥러닝: 네트워크의 중간 층의 활성화 값에도 적용
학습 가능성:
- 전통적 ML: 고정된 변환
- 딥러닝: 학습 가능한 파라미터를 포함하는 경우가 많음
목적의 확장:
- 전통적 ML: 주로 데이터 스케일 조정에 초점
- 딥러닝: 내부 공변량 변화 감소, 기울기 소실/폭발 문제 해결 등 추가적인 목적 포함

이러한 차이점을 인식하고 각 상황에 맞는 정규화 기법을 선택하는 것이 중요합니다. 이 글에서는 딥러닝에서 주로 사용되는 정규화 기법들에 대해 자세히 알아보겠습니다.

주로 사용되는 방법:

배치 정규화 (Batch Normalization)
레이어 정규화 (Layer Normalization)
인스턴스 정규화 (Instance Normalization)
그룹 정규화 (Group Normalization)
RMS 정규화 (RMS Normalization)

배치 정규화 (Batch Normalization)

개념

배치 정규화는 2015년 Sergey Ioffe와 Christian Szegedy가 제안한 기법으로, 신경망의 각 층에서 입력을 정규화하는 방법입니다.

작동 원리

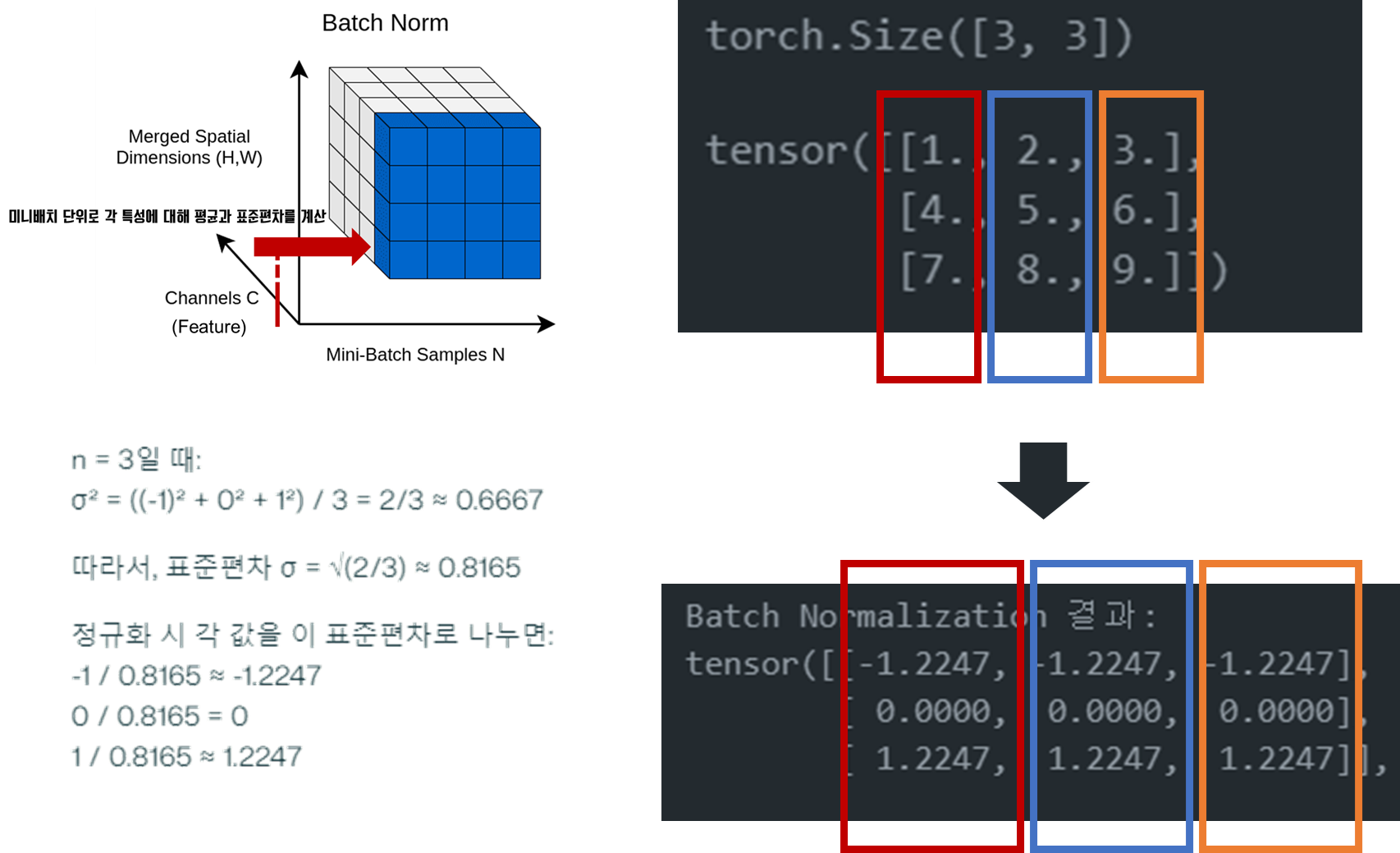
미니배치 단위로 평균과 분산을 계산합니다.
입력값을 정규화합니다.
스케일(γ)과 시프트(β) 파라미터를 적용합니다.

각 레이어/채널마다 다른 γ와 β를 사용함으로써, 네트워크는 각 레이어의 특성과 역할에 맞는 최적의 정규화를 학습할 수 있습니다.

수식

y=γ∗((x−μB)/sqrt(σB2+ε))+βy = γ * ((x - μ_B) / sqrt(σ_B^2 + ε)) + βy=γ∗((x−μB)/sqrt(σB2+ε))+β

여기서 μBμ_BμB는 배치 평균, σB2σ_B^2σB2는 배치 분산, ε은 작은 상수, γ와 β는 학습 가능한 파라미터입니다.

예시

# 입력 배치
import torch
import torch.nn as nn

X = torch.tensor([[1,2,3],
                  [4,5,6],
                  [7,8,9]], dtype=torch.float32)

print(X.shape)
print(X)
# torch.Size([3, 3])
# tensor([[1., 2., 3.],
#         [4., 5., 6.],
#         [7., 8., 9.]])

# 3은 특성(feature) 수
bn = nn.BatchNorm1d(3)  
output_bn = bn(X)
print("Batch Normalization 결과:")
print(output_bn)

# Batch Normalization 결과:
# tensor([[-1.2247, -1.2247, -1.2247],
#         [ 0.0000,  0.0000,  0.0000],
#         [ 1.2247,  1.2247,  1.2247]], grad_fn=<NativeBatchNormBackward0>)

# 직접 구현
def batch_norm(X, eps=1e-5):
    mean = X.mean(dim=0, keepdim=True)
    var = X.var(dim=0, unbiased=False, keepdim=True)
    X_norm = (X - mean) / torch.sqrt(var + eps)
    return X_norm

print("Batch Normalization 결과:")
print(batch_norm(X))

# Batch Normalization 결과:
# tensor([[-1.2247, -1.2247, -1.2247],
#         [ 0.0000,  0.0000,  0.0000],
#         [ 1.2247,  1.2247,  1.2247]])

장단점

장점:
- 학습 속도 향상
- 내부 공변량 변화(Internal Covariate Shift) 감소
- 더 높은 학습률 사용 가능
단점:
- 작은 미니배치에서 불안정할 수 있음
- 순환 신경망(RNN)에 적용하기 어려움

응용 사례

CNN 모델에서 주로 사용
EfficientNet: 이미지 분류를 위한 CNN 아키텍처
BERT: 자연어 처리를 위한 트랜스포머 기반 모델

레이어 정규화 (Layer Normalization)

개념

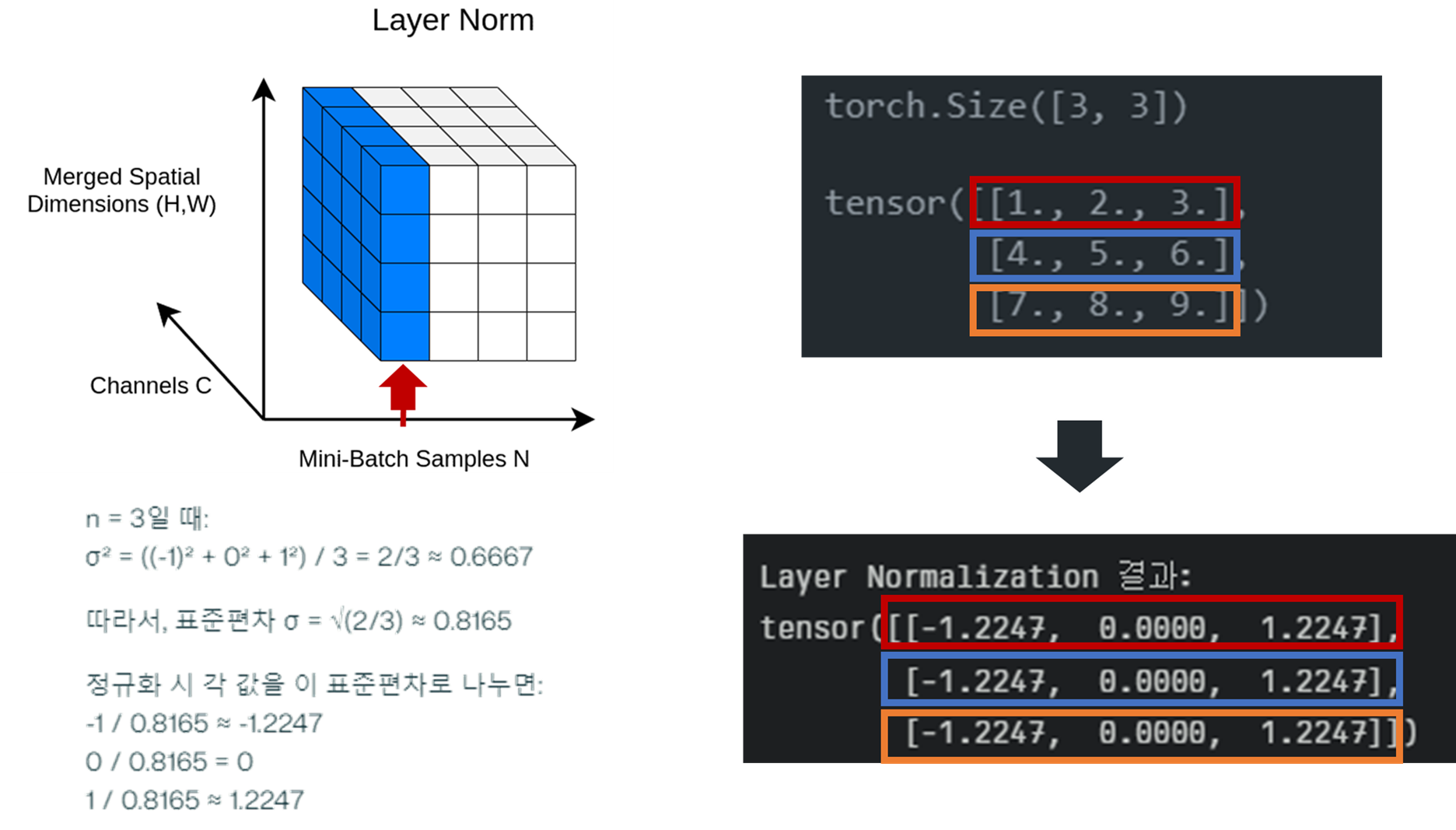
레이어 정규화는 2016년 Jimmy Lei Ba 등이 제안한 기법으로, 각 샘플에 대해 모든 뉴런의 출력을 정규화합니다.

작동 원리

각 샘플에 대해 모든 뉴런 출력의 평균과 분산을 계산합니다.
계산된 평균과 분산으로 입력을 정규화합니다.
스케일(γ)과 시프트(β) 파라미터를 적용합니다.

수식

다음은 레이어 정규화의 수식입니다:

y=γ∗((x−μL)/sqrt(σL2+ε))+βy = γ * ((x - μ_L) / sqrt(σ_L^2 + ε)) + βy=γ∗((x−μL)/sqrt(σL2+ε))+β

여기서 μLμ_LμL은 레이어 평균, σL2σ_L^2σL2는 레이어 분산입니다.

예시

# 입력 배치
import torch
import torch.nn as nn

X = torch.tensor([[1,2,3],
                  [4,5,6],
                  [7,8,9]], dtype=torch.float32)

print(X.shape)
print(X)
# torch.Size([3, 3])
# tensor([[1., 2., 3.],
#         [4., 5., 6.],
#         [7., 8., 9.]])

ln = nn.LayerNorm(3)  # 3은 정규화할 마지막 차원의 크기
output_ln = ln(X)
print("Layer Normalization 결과:")
print(output_ln)

# Layer Normalization 결과:
# tensor([[-1.2247,  0.0000,  1.2247],
#         [-1.2247,  0.0000,  1.2247],
#         [-1.2247,  0.0000,  1.2247]], grad_fn=<NativeLayerNormBackward0>)

def layer_norm(X, eps=1e-5):
    mean = X.mean(dim=-1, keepdim=True)
    var = X.var(dim=-1, unbiased=False, keepdim=True)
    X_norm = (X - mean) / torch.sqrt(var + eps)
    return X_norm

print("Layer Normalization 결과:")
print(layer_norm(X))

# Layer Normalization 결과:
# tensor([[-1.2247,  0.0000,  1.2247],
#         [-1.2247,  0.0000,  1.2247],
#         [-1.2247,  0.0000,  1.2247]])

장단점

장점:
- 배치 크기에 독립적
- RNN에 적용 가능
- 자연어 처리 작업에 효과적
단점:
- CNN에서는 배치 정규화보다 성능이 떨어질 수 있음

응용 사례

RNN, 트랜스포머 모델에서 주로 사용
GPT (Generative Pre-trained Transformer) 시리즈
ALBERT (A Lite BERT)

인스턴스 정규화 (Instance Normalization)

개념

인스턴스 정규화는 2016년 Dmitry Ulyanov 등이 제안한 기법으로, 주로 스타일 전이 작업에 사용됩니다.

작동 원리

각 샘플의 각 채널에 대해 평균과 분산을 계산합니다.
계산된 평균과 분산으로 입력을 정규화합니다.
스케일(γ)과 시프트(β) 파라미터를 적용합니다.

수식

ynchw=γ∗((xnchw−μnc)/sqrt(σnc2+ε))+βy_nchw = γ * ((x_nchw - μ_nc) / sqrt(σ_nc^2 + ε)) + βynchw=γ∗((xnchw−μnc)/sqrt(σnc2+ε))+β

여기서 n은 샘플, c는 채널, h와 w는 높이와 너비를 나타냅니다.

예시

# 입력 (2개의 샘플, 각 2x2 크기, 4 채널)
X = torch.tensor([[
                  [[1, 2], [3, 4]],
                  [[5, 6], [7, 8]],
                  [[9, 10], [11, 12]],
                  [[13, 14], [15, 16]]
                  ],
                  [
                  [[17, 18], [19, 20]],
                  [[21, 22], [23, 24]],
                  [[25, 26], [27, 28]],
                  [[29, 30], [31, 32]]
                  ]], dtype=torch.float32)
print(X.shape)
# torch.Size([2, 4, 2, 2])
# tensor([[[[ 1.,  2.],
#           [ 3.,  4.]],
# 
#          [[ 5.,  6.],
#           [ 7.,  8.]],
# 
#          [[ 9., 10.],
#           [11., 12.]],
# 
#          [[13., 14.],
#           [15., 16.]]],
# 
# 
#         [[[17., 18.],
#           [19., 20.]],
# 
#          [[21., 22.],
#           [23., 24.]],
# 
#          [[25., 26.],
#           [27., 28.]],
# 
#          [[29., 30.],
#           [31., 32.]]]])

# Instance Normalization은 주로 2D나 3D 데이터에 사용되지만, 
# InstanceNorm2d 적용 (4은 채널 수)
in_norm = nn.InstanceNorm2d(4, affine=True)
output_in = in_norm(X)
print("Instance Normalization 결과 (PyTorch):")
print(output_in)

# Instance Normalization 결과 (PyTorch):
# tensor([[[[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]],
# 
#          [[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]],
# 
#          [[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]],
# 
#          [[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]]],
# 
# 
#         [[[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]],
# 
#          [[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]],
# 
#          [[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]],
# 
#          [[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]]]], grad_fn=<ViewBackward0>)

def instance_norm(X, eps=1e-5):
    mean = X.mean(dim=(2, 3), keepdim=True)
    var = X.var(dim=(2, 3), unbiased=False, keepdim=True)
    X_norm = (X - mean) / torch.sqrt(var + eps)
    return X_norm

print("Instance Normalization 결과 (수동 구현):")
print(instance_norm(X))

# Instance Normalization 결과 (수동 구현):
# tensor([[[[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]],
# 
#          [[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]],
# 
#          [[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]],
# 
#          [[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]]],
# 
# 
#         [[[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]],
# 
#          [[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]],
# 
#          [[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]],
# 
#          [[-1.3416, -0.4472],
#           [ 0.4472,  1.3416]]]])

🔎 왜 dim = (2,3)인가?

✍️ dim=(2, 3)은 텐서의 마지막 두 차원(높이와 너비)에 대해 평균과 분산을 계산하라는 의미입니다.

텐서 형태: (배치, 채널, 높이, 너비)

dim=0: 배치 차원

dim=1: 채널 차원

dim=2: 높이 차원

dim=3: 너비 차원

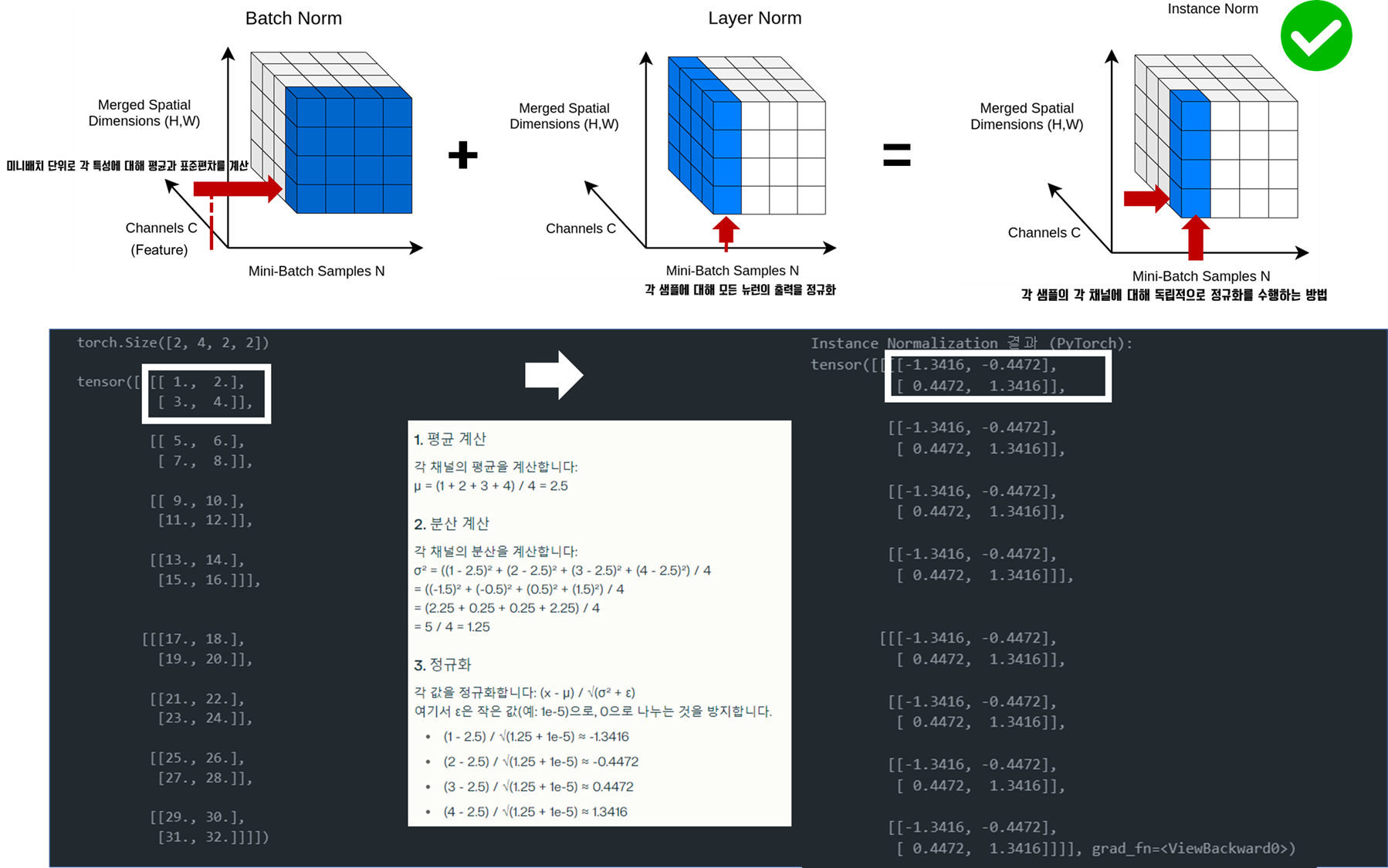
(더하기는 확장의 개념이지 실제 더했다는 의미가 아닙니다 ><)

장단점

장점:
- 스타일 전이 작업에 효과적
- 배치 크기에 독립적
단점:
- 채널 간 정보를 고려하지 않음

응용 사례

스타일 전이(Style Transfer) 계열 모델
이미지 생성 모델: GAN(Generative Adversarial Networks) 계열 모델

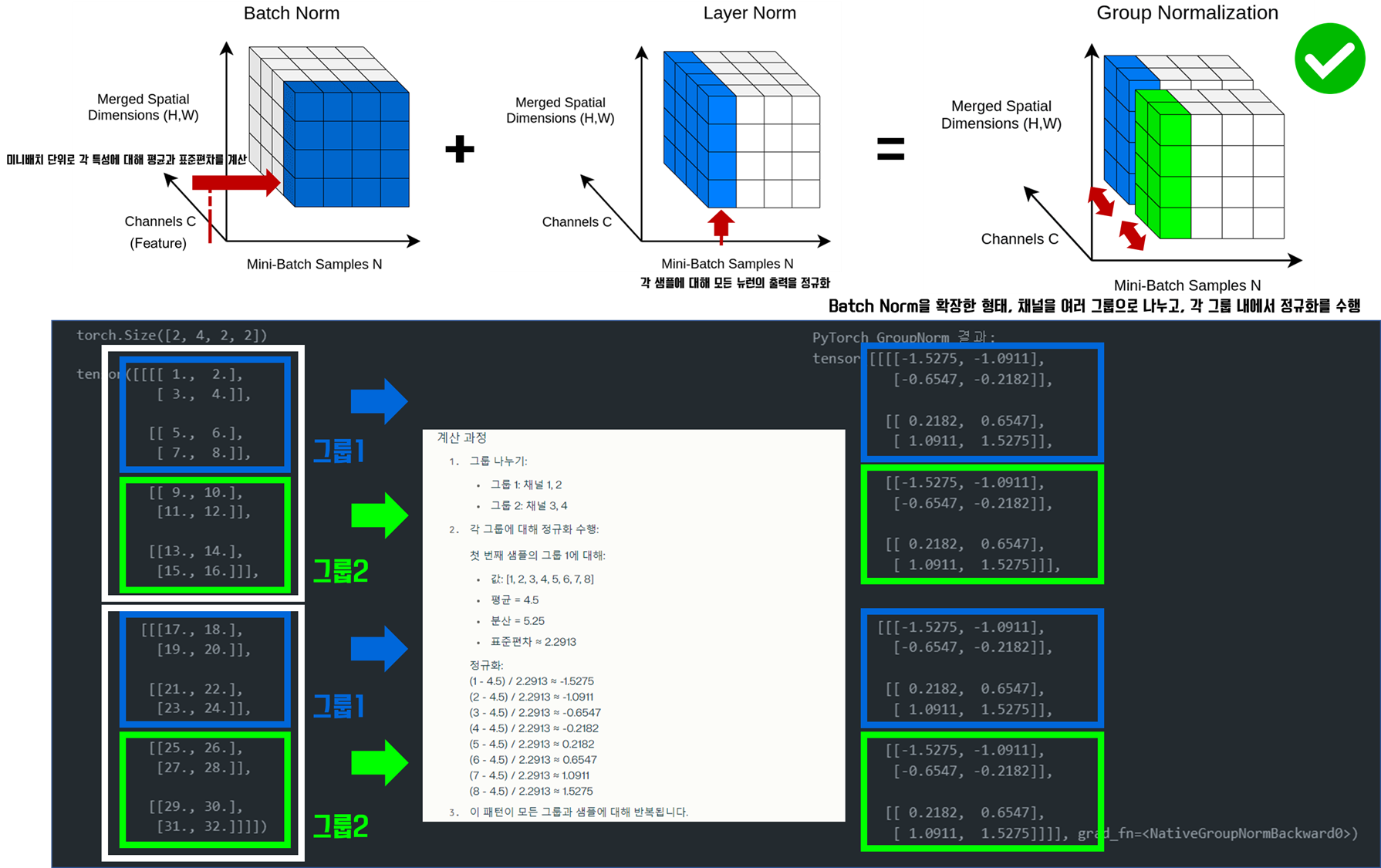
그룹 정규화(Group Normalization)

Group Normalization은 2018년 Yuxin Wu와 Kaiming He가 제안한 정규화 기법입니다. 이 기법은 Batch Normalization (BN)의 한계를 극복하기 위해 개발되었습니다.

BN의 주요 한계점

작은 배치 크기에서 성능 저하
배치 통계에 의존하여 배치 간 변동성이 큼

작동 원리

GN은 채널을 여러 그룹으로 나누고, 각 그룹 내에서 정규화를 수행합니다.
채널 그룹화: 입력 특성의 채널을 G개의 그룹으로 나눕니다.
그룹별 정규화: 각 그룹 내에서 평균과 표준편차를 계산하여 정규화합니다.
정규화된 값에 학습 가능한 스케일(γ)과 시프트(β) 파라미터를 적용합니다.

수식

μ = (1/m) *Σx

σ² = (1/m)* Σ(x - μ)²

y = (x - μ) / √(σ² + ε)

여기서 m은 그룹 내 원소의 수, ε은 작은 상수입니다.

예시

import torch
import torch.nn as nn

# 입력 (2개의 샘플, 각 2x2 크기, 4 채널)
X = torch.tensor([[
                  [[1, 2], [3, 4]],
                  [[5, 6], [7, 8]],
                  [[9, 10], [11, 12]],
                  [[13, 14], [15, 16]]
                  ],
                  [
                  [[17, 18], [19, 20]],
                  [[21, 22], [23, 24]],
                  [[25, 26], [27, 28]],
                  [[29, 30], [31, 32]]
                  ]], dtype=torch.float32)
print(X.shape)

def group_norm_pytorch(X, num_groups=2):  # 그룹 수를 2으로 변경
    # num_groups: 그룹의 수
    # num_channels: 채널의 수 (X의 두 번째 차원)
    num_channels = X.shape[1]
    gn = nn.GroupNorm(num_groups, num_channels)
    return gn(X)

# PyTorch GroupNorm 적용
gn_pytorch = group_norm_pytorch(X)
print("\nPyTorch GroupNorm 결과:")
print(gn_pytorch)


# PyTorch GroupNorm 결과:
# tensor([[[[-1.5275, -1.0911],
#           [-0.6547, -0.2182]],
# 
#          [[ 0.2182,  0.6547],
#           [ 1.0911,  1.5275]],
# 
#          [[-1.5275, -1.0911],
#           [-0.6547, -0.2182]],
# 
#          [[ 0.2182,  0.6547],
#           [ 1.0911,  1.5275]]],
# 
# 
#         [[[-1.5275, -1.0911],
#           [-0.6547, -0.2182]],
# 
#          [[ 0.2182,  0.6547],
#           [ 1.0911,  1.5275]],
# 
#          [[-1.5275, -1.0911],
#           [-0.6547, -0.2182]],
# 
#          [[ 0.2182,  0.6547],
#           [ 1.0911,  1.5275]]]], grad_fn=<NativeGroupNormBackward0>)

(더하기는 확장의 개념이지 실제 더했다는 의미가 아닙니다 ><)

장단점

장점
- 배치 크기에 독립적으로 동작합니다.
- 작은 배치 크기에서도 안정적으로 동작합니다.
- CNN에서 배치 정규화를 대체할 수 있습니다.
단점
- 그룹 수를 추가적인 하이퍼파라미터로 설정해야 합니다.

활용 사례

객체 탐지 및 세그먼테이션 모델에서 널리 사용됩니다.
소규모 배치를 사용하는 고해상도 이미지 처리 작업에 적합합니다.

RMS 정규화 (RMS Normalization)

개념

RMS Norm (Root Mean Square Layer Normalization)은 2019년 Biao Zhang과 Rico Sennrich가 발표한 논문 “Root Mean Square Layer Normalization”에서 처음 소개되었습니다. RMS 정규화는 최근 대규모 언어 모델에서 주목받고 있는 기법으로, 레이어 정규화를 간소화한 버전입니다.

작동 원리

각 샘플에 대해 모든 특성의 제곱평균제곱근(RMS)을 계산합니다.
계산된 RMS 값으로 입력을 나눕니다.
스케일(γ) 파라미터를 적용합니다.

수식

y=x/√(mean(x²)+ε)y = x / √(mean(x²) + ε)y=x/√(mean(x²)+ε)

여기서 x는 입력, ε은 작은 상수입니다.

💡 RMS vs Layer Norm

Layer Norm과 RMS Norm의 주요 차이점:

중심화(centering) 제거:

Layer Norm: (x - μ) / √(σ² + ε)

RMS Norm: x / √(mean(x²) + ε)

분산 계산 방식:

Layer Norm: σ² = mean((x - μ)²)

RMS Norm: mean(x²)를 직접 사용

🔎 RMS로 나누는 의미

계산 효율성: mean(x²)는 σ²보다 계산이 간단합니다.

스케일 불변성 유지: 입력의 스케일에 관계없이 일정한 출력 범위를 유지합니다.

정규화 효과: 입력을 적절한 범위로 조정하여 학습 안정성을 높입니다.

예시

import torch
import torch.nn as nn

X = torch.tensor([[1,2,3],
                  [4,5,6],
                  [7,8,9]], dtype=torch.float32)
print(X)
# tensor([[1., 2., 3.],
#         [4., 5., 6.],
#         [7., 8., 9.]])

def rms_norm(X, eps=1e-8):
    rms = torch.sqrt(torch.mean(X**2, dim=-1, keepdim=True) + eps)
    X_norm = X / rms
    return X_norm

print("RMS Normalization 결과:")
print(rms_norm(X))

# RMS Normalization 결과:
# tensor([[0.4629, 0.9258, 1.3887],
#         [0.7895, 0.9869, 1.1843],
#         [0.8705, 0.9948, 1.1192]], grad_fn=<MulBackward0>)

장단점

장점:
- 계산 효율성이 높음
- 대규모 모델에 적합
- 평균을 계산하지 않아 더 안정적
단점:
- 레이어 정규화에 비해 표현력이 다소 제한될 수 있음

응용 사례

PaLM (Pathways Language Model)
LLaMA (Large Language Model Meta AI)

정규화 기법 비교

각 정규화 기법은 서로 다른 특성과 장단점을 가지고 있습니다. 아래 표는 이들을 간단히 비교한 것입니다:

기법	계산 단위	장점	단점	주요 응용 분야
배치 정규화	미니배치	학습 속도 향상, 높은 학습률 사용 가능	작은 배치에서 불안정, RNN에 적용 어려움	CNN, 이미지 처리
레이어 정규화	개별 샘플	배치 크기 독립적, RNN에 적용 가능	CNN에서 성능 저하 가능	RNN, 자연어 처리
인스턴스 정규화	개별 샘플의 채널	스타일 전이에 효과적, 배치 크기 독립적	채널 간 정보 무시	스타일 전이, 이미지 생성
그룹 정규화	채널 그룹	배치 크기 독립적, 작은 배치에서도 안정적	그룹 수 선택이 성능에 영향	객체 탐지, 세그멘테이션
RMS 정규화	개별 샘플	계산 효율성 높음, 대규모 모델에 적합	표현력 다소 제한	대규모 언어 모델

결론

정규화 기법은 딥러닝 모델의 성능을 크게 향상시키는 중요한 요소입니다. 각 기법은 고유한 특성과 장단점을 가지고 있어, 작업의 성격과 모델 구조에 따라 적절한 기법을 선택하는 것이 중요합니다. 최근에는 이러한 기본적인 정규화 기법들을 조합하거나 변형하여 더 나은 성능을 얻으려는 연구도 활발히 진행되고 있습니다.

딥러닝 분야가 빠르게 발전함에 따라, 새로운 정규화 기법들이 계속해서 제안되고 있습니다. 따라서 최신 연구 동향을 주시하고, 자신의 작업에 가장 적합한 정규화 기법을 실험을 통해 찾아내는 것이 중요합니다.

중요한 개념이기에 그만큼 시간을 들여서 열심히 작성해봤는데요! 도움이 되셨으면 좋겠습니다 🤗

[개념] Deep Learning Normalization Techniques

[개념] Deep Learning Normalization Techniques

딥러닝에서의 정규화 기법

정규화의 정의와 목적

머신러닝에서의 정규화

딥러닝에서의 정규화

주요 차이점

배치 정규화 (Batch Normalization)

레이어 정규화 (Layer Normalization)

인스턴스 정규화 (Instance Normalization)

그룹 정규화(Group Normalization)

RMS 정규화 (RMS Normalization)

정규화 기법 비교

결론

CATALOG

FEATURED TAGS

FRIEND SITES