[머신러닝][시계열] AR, MA, ARMA, ARIMA의 모든 것 - 개념편
오늘은 머신러닝 시계열에서 가장 많이 쓰이는 AR, MA, ARMA, ARIMA에 대해 정리해보는 시간을 가지려고 합니다. 해당 포스트는 고려대학교 김성범 교수님의 강의를 바탕으로 제작되었습니다.
목차
- 정상 프로세스와 비정상 프로세스
- Autoregressive (AR) Models
- Moving Average (MA) Models
- Autoregressive and Moving Average (ARMA)
- Autoregressive Integrated Moving Average (ARIMA)
-
ACF(자기상관함수)와 PACF(부분자기상관함수)
-
정상 프로세스와 비정상 프로세스
(1) Stationary Process (정상 프로세스) : 시간에 관계없이 평균과 분산이 일정한 시계열 데이터를 의미합니다.
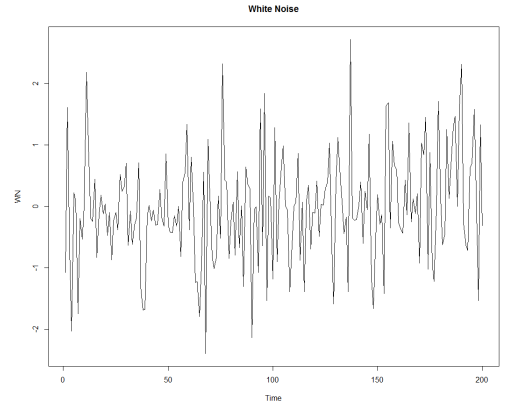
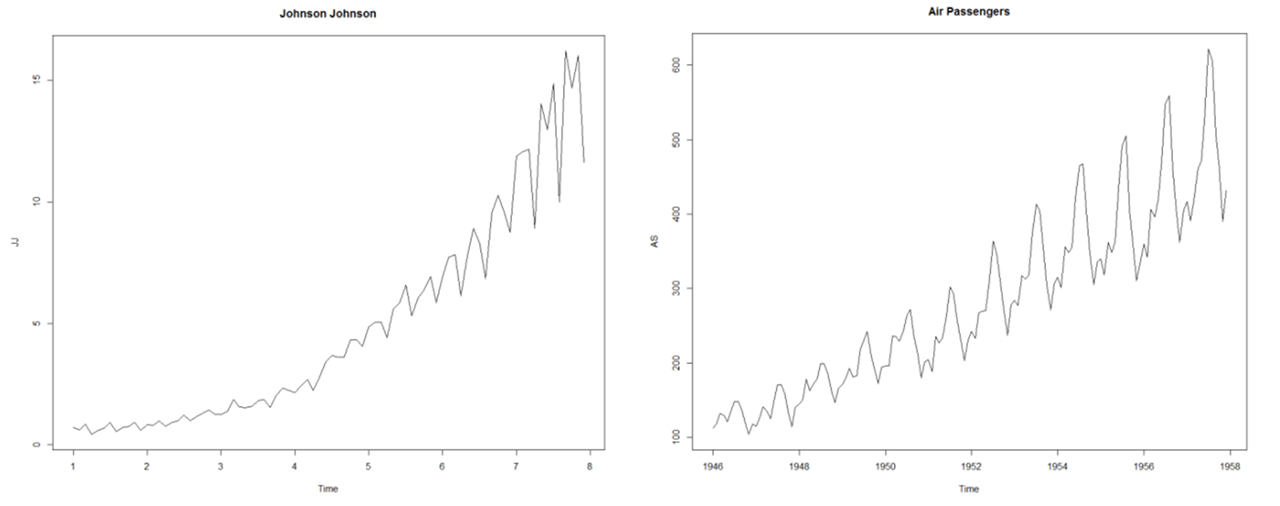
(2) Non-Stationary Process (비정상 프로세스) : 시간에 관계없이 평균과 분산이 일정하지 않은 시계열 데이터를 의미합니다.
📕 여기서 잠깐! 그렇다면 어떻게 정상과 비정상 프로세스를 비교할까요?
X축을 Lag (현재 데이터와의 시점 차이)로 Y축을 ACF(Autocorrelation Function)으로 시각화 하였을 때 특정 패턴이 없으면 Stationary Process (정상 프로세스)로 볼 수 있습니다.
🤔 오호라.. 그렇다면 AC(Autocorrelation)은 도대체 뭐죠?
우리가 많이 접해본 Correlation은 두 변수 사이의 관계를 -1 ~ 1의 값으로 표현하는 척도입니다. Autocorrealation은 Correlation에 Auto라는 개념이 추가된 것으로, 쉽게 설명하자면 시계열적 관점으로 보았을 때 time shifted된 자기 자신과의 correlation을 의미합니다.
-
Autoregressive (AR) Models
자기자신을 종속변수(dependent variable) yty_tyt로 하고, 이전 시점의 시계열(Lag) [yt−1,yt−2,…,yt−p][y_{t-1}, y_{t-2} , …, y_{t-p}][yt−1,yt−2,…,yt−p] 를 독립변수(independent variable)로 갖는 모델(model that use lags of the dependent variable as independent variables)을 의미합니다.
yt=∅0+∅1yt−1+∅2yt−2+…+∅pyt−p+εty_{t}=\emptyset_{0}+\emptyset_{1} y_{t-1}+\emptyset_{2} y_{t-2}+\ldots+\emptyset_{p} y_{t-p}+\varepsilon_{t}yt=∅0+∅1yt−1+∅2yt−2+…+∅pyt−p+εt
Hyperparameter : p
-
Moving Average (MA) Models
자기자신을 종속변수(dependent variable) yty_tyt로 하고, 해당 시점과 그 과거의 white noise distribution error들로, [εt,εt−1,…,εt−q][ε_{t}, ε_{t-1}, …, ε_{t-q}][εt,εt−1,…,εt−q]를 독립변수(independent variable)로 갖는 모델 (model that use past errors that follow a white noise distribution as explanatory variables)을 의미합니다.
yt=θ0+εt+θ1εt−1+θ2εt−2+…+θqεt−qy_{t}=\theta_{0}+\varepsilon_{t}+\theta_{1} \varepsilon_{t-1}+\theta_{2} \varepsilon_{t-2}+\ldots+\theta_{q} \varepsilon_{t-q}yt=θ0+εt+θ1εt−1+θ2εt−2+…+θqεt−q
Hyperparameter : q
-
Autoregressive and Moving Average (ARMA)
자기자신을 종속변수(dependent variable) yty_tyt로 하고, 이전 시점의 시계열(Lag) [yt−1,yt−2,…,yt−p][y_{t-1}, y_{t-2} , …, y_{t-p}][yt−1,yt−2,…,yt−p]과 [εt,εt−1,…,εt−q][ε_{t}, ε_{t-1}, …, ε_{t-q}][εt,εt−1,…,εt−q]를 독립변수(independent variable)로 갖는 모델로, ARMA라는 이름에서도 알 수 있듯이 AR과 MA를 합친 모델입니다.
yt=∅0+∅1yt−1+∅2yt−2+⋯∅pyt−p+εt+θ1εt−1+θ2εt−2+…+θqεt−qy_{t}=\emptyset_{0}+\emptyset_{1} y_{t-1}+\emptyset_{2} y_{t-2}+\cdots \emptyset_{p} y_{t-p}+\varepsilon_{t}+\theta_{1} \varepsilon_{t-1}+\theta_{2} \varepsilon_{t-2}+\ldots+\theta_{q} \varepsilon_{t-q}yt=∅0+∅1yt−1+∅2yt−2+⋯∅pyt−p+εt+θ1εt−1+θ2εt−2+…+θqεt−q
Hyperparameter : p, q
-
Autoregressive Integrated Moving Average (ARIMA)
기존 AR, MA, ARMA 모델의 경우 데이터가 정상 (Stationary)이어야 함으로 비정상 (Nonstationary)인 경우는 차분 (differencing)을 통해 데이터를 정상으로 변형해주어야 합니다. ARIMA는 ARMA 모형에 차분을 d회 수행해준 모델입니다.
Hyperparameter : p, q, d
📕 여기서 잠깐! 차분 (differencing)이란 뭘까요?
차분 (differencing)이란, 현 시점 데이터에서 d시점 이전 데이터를 뺀 것입니다. 아래 그림과 식을 통해 간단하게 어떤 메커니즘인지 이해하실 수 있으실 겁니다.

1차 차분 : Yt=Xt−Xt−1=∇XtY_{t}=X_{t}-X_{t-1}=\nabla X_{t}Yt=Xt−Xt−1=∇Xt
2차 차분 : Yt(2)=Xt−Xt−2=∇(2)XtY_{t}^{(2)}=X_{t}-X_{t-2}=\nabla^{(2)} X_{t}Yt(2)=Xt−Xt−2=∇(2)Xt
3차 차분 : Yt(d)=Xt−Xt−d=∇(d)XtY_{t}^{(d)}=X_{t}-X_{t-d}=\nabla^{(d)} X_{t}Yt(d)=Xt−Xt−d=∇(d)Xt
아래는 각각 1차 차분, 2차 차분 수행 결과를 시각화한 결과입니다. 일반적으로 시계열 곡선이 특정한 트렌드(constant average trend)를 가지고 있다면 1차 차분을, 시간에 따라 들쑥날쑥한 트렌드가 있다면 2차 차분을 통상적으로 수행합니다.
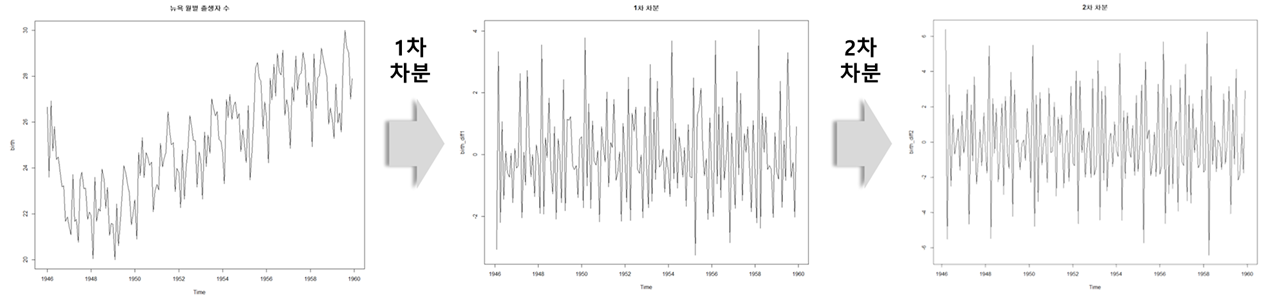
-
ACF(자기상관함수)와 PACF(부분자기상관함수)
ACF(AutoCorrelation Function)이란?
ACF(AutoCorrelation Function, 자기상관함수) 는 k시간 단위로 구분된 시계열의 관측치 간 상관계수 함수를 의미하며, k가 커질수록 ACF는 0에 가까워집니다.
이 때, ACF를 구하는 식은 일반 Correlation 구하는 식과 동일합니다. 다음은 yty_{t}yt와 yt−ky_{t-k}yt−k 사이의 자기상관을 구하는 식입니다.
ACF(k)=∑t=1N−k(yt−yˉ)(yt+k−yˉ)∑t=1N(yt−yˉ)2A C F(k)=\frac{\sum_{t=1}^{N-k}\left(y_{t}-\bar{y}\right)\left(y_{t+k}-\bar{y}\right)}{\sum_{t=1}^{N}\left(y_{t}-\bar{y}\right)^{2}}ACF(k)=∑t=1N(yt−yˉ)2∑t=1N−k(yt−yˉ)(yt+k−yˉ)
PACF(Partial ACF)이란?
먼저 부분 상관 (Partial Correlation) 이란 두 확률 변수 X와 Y에 의해 다른 모든 변수들에 나타난 상관 관계를 설명하고 난 이후에도 여전히 남아있는 상관 관계라고 정의할 수 있습니다.
따라서, 부분자기상관함수 (PACF) 는 자기상관함수와 마찬가지로 시계열 관측지 간 상관 관계 함수이고, 시차 k에서의 k단계만큼 떨어져 있는 모든 데이터 점들간의 순수한 상관 관계를 말합니다. 다시말해 yty_{t}yt와 yt−ky_{t-k}yt−k의 PACF는, yty_{t}yt와 yt−ky_{t-k}yt−k간의 순수한 상관관계로서 두 시점 사이에 포함된 모든 yt−1,yt−2,…,yt−k+1y_{t-1}, y_{t-2}, \ldots, y_{t-k+1}yt−1,yt−2,…,yt−k+1의 영향력은 제거됨을 의미합니다.
다음은 yty_{t}yt와 yt−ky_{t-k}yt−k 사이의 편자기상관을 구하는 식입니다.
PACF(k)=Corr(et,et−k)P A C F(k)=\operatorname{Corr}\left(e_{t}, e_{t-k}\right)PACF(k)=Corr(et,et−k)
어떻게 사용되는가?
ACF와 PACF의 모양을 통해 ARIMA(AR, MA, ARMA) 모델의 하이퍼파라미터인 p와 q를 결정하는데 그 방법은 아래 표와 같습니다.
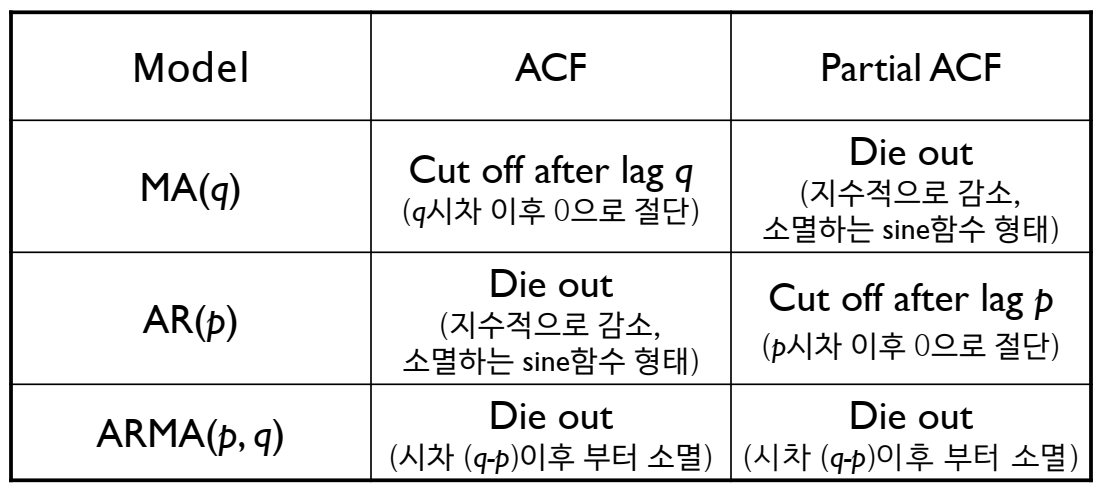
긴 글 읽어주셔서 감사합니다 ^~^