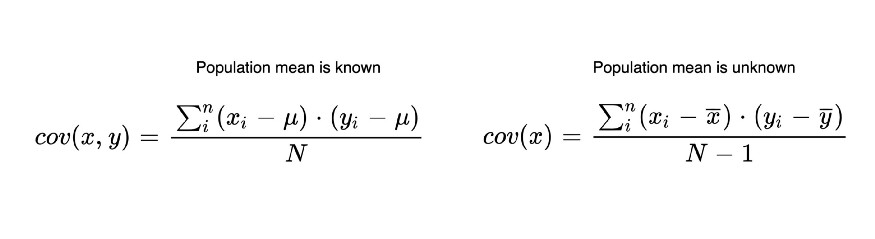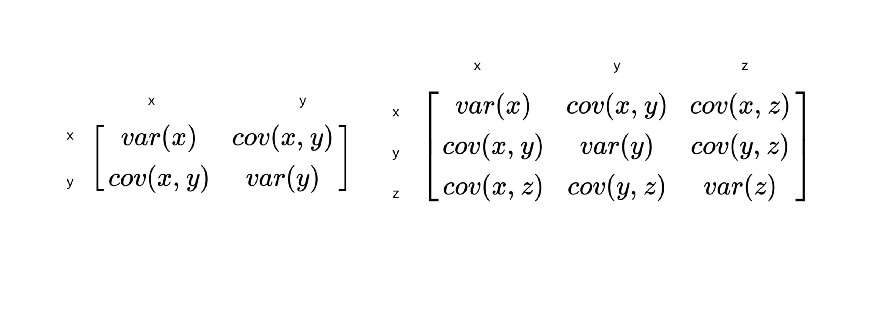[머신러닝][차원축소] 변수 추출법 - Principal Component Analysis (PCA)

본 포스트는 고려대학교 강필성 교수님의 강의를 수강 후 정리를 한 것입니다.

작성 및 설명의 편의를 위해 아래는 편하게 작성한 점 양해부탁드립니다.

Dimensionality Reduction

Supervised Variable Extraction

차원축소는, 모델링을 하기 위해 내가 가진 데이터의 정보를 최대한 보존하면서, 훨씬 더 compact하게 데이터셋을 구성하는 것을 목적으로 하며, 크게 변수선택(Variable Selection, 변수들의 부분 집합 선택)과 변수추출(Variable Extraction, 변수들을 요약하는 새로운 변수 생성)이 있다.

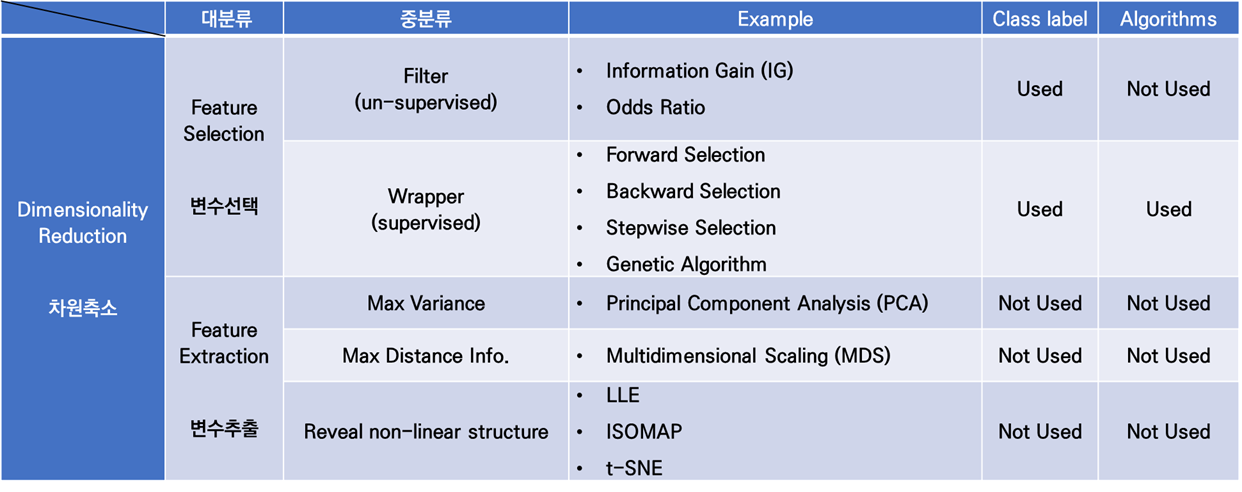
이전 포스트에서는 아래 표에서 Supervised Variable Selection을 살펴보았다. 오늘은 Supervised Variable Extraction에 대해 이야기를 풀어보도록 하겠다.

Principal Component Analysis

Principal Component Analysis (PCA)는 변수추출의 대표적인 기법으로, 주성분분석으로도 불리며, original data의 분산을 최대한 보존(preserve the variance)하는 직교 기저(orthogonal basis)를 찾는 방법이다.

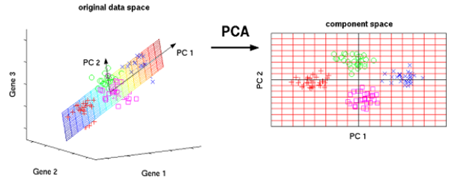
Q. 다음 밑에 두 가지의 그림은 위의 그림을 사영시킨 기저들이다. 이때, 기저는 각각의 데이터들이 사영이 되는 대상의 벡터를 의미한다. 그렇다면 분산(Variance)을 잘 보존한다는 무슨 의미일까?

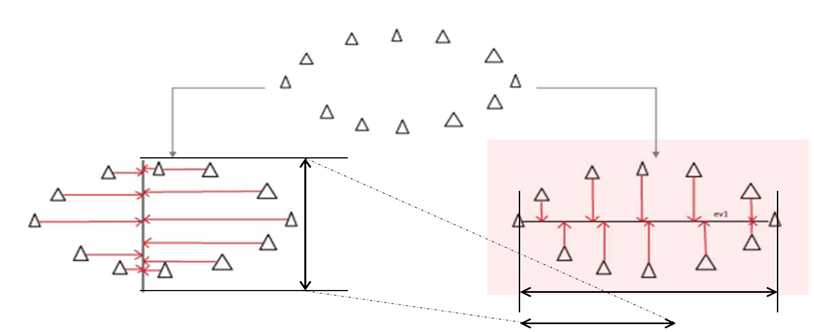
분산량(variability)은 각각 기저들에 사영된 점들의 흩어진 정도를 의미한다. 이를 잘 보존한다는 것은 원래 데이터가 가지고 있었던 분산량을 얼만큼 잘 간직하는가를 의미한다. 따라서, 위 그림은 각각 X축과 Y축을 기저로 사영한 것이며, 이들은 각각 사영 전의 데이터의 분산을 보존하는 것을 확인할 수 있다.

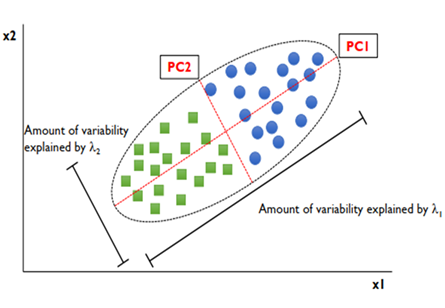
PCA는, 사영 후 가능한 한 많은 분산을 보존할 수 있는 기저들의 집합을 구하는 것 (find a set of basis that can preserve the variance as much as possible after the projection on the basis) 을 목적으로 한다.

(참고) Covariance Matrix

• 정의 :
  두 변수 이상의 다변량 값들 간의 공분산들을 행렬로 표현한 것을 의미한다.

💡 공분산 수식

💡 2변량, 3변량 공분산 행렬

• 표기 :

  • X:X :X: column-wise 데이터셋 (d x n ; d는 변수의 수, n은 record의 수)
  • Cov⁡(X):1n(X−Xˉ)(X−Xˉ)T,( d×n)∗(n×d)=(d×d)\operatorname{Cov}(X):\frac{1}{n}(X-\bar{X})(X-\bar{X})^{T}, (\mathrm{~d} \times n) *(n \times \mathrm{d})=(\mathrm{d} \times \mathrm{d})Cov(X):n1​(X−Xˉ)(X−Xˉ)T,( d×n)∗(n×d)=(d×d)

• 특징 :

  1. 대칭행렬
     Cov⁡(Xij)=Cov⁡(Xji)\operatorname{Cov}(X_{ij}) = \operatorname{Cov}(X_{ji})Cov(Xij​)=Cov(Xji​)
  2. 데이터셋의 총 분산량 = 대각행렬의 합
     tr⁡(Cov⁡(X))=Cov⁡(X)11+Cov⁡(X)22+⋯+Cov⁡(X)dd\operatorname{tr}(\operatorname{Cov}(X))=\operatorname{Cov}(X)_{11}+\operatorname{Cov}(X)_{22}+\cdots+\operatorname{Cov}(X)_{d d}tr(Cov(X))=Cov(X)11​+Cov(X)22​+⋯+Cov(X)dd​

(참고) Projection

• 정의 :
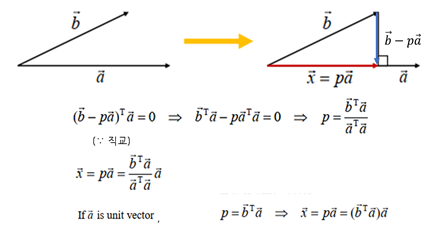
  한 점에서 한 직선 또는 한 평면에 수선의 발을 내릴 때 이를 Projection(사영)한다고 한다.

(참고) Eigen-Value & Eigen-Vector

• 행렬 A가 주어졌을 때, 다음을 만족하는 스칼라 λ 값과 벡터 x를 각각 고유값(Eigen-Value)과 고유벡터(Eigen-Vector)라고 정의한다.

Ax=λx→(A−λI)x=0\mathbf{A x}=\lambda \mathbf{x} \quad \rightarrow \quad(\mathrm{A}-\lambda \mathrm{I}) \mathbf{x}=0Ax=λx→(A−λI)x=0

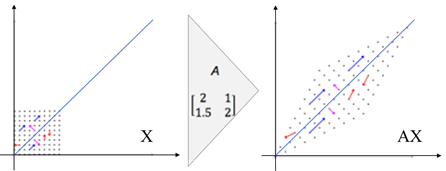
• 벡터에 행렬을 곱한다는 것은 선형변환(linear transformation)을 수행한다는 것이다. 밑의 그림을 보면 크기만 바뀌고 방향이 바뀌지 않는 벡터(파랑, 핑크)가 있는 것을 확인할 수 있는데 이를 “고유벡터”라고 하고, 이때 크기가 λ배 바뀐 것을 확인할 수 있는데 이를 “고유값”이라고 한다.

• 행렬 A (dxd)가 역행렬이 존재한다면, 고유값과 고유벡터는 다음 성질을 갖는다.

  

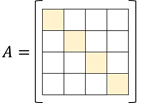
  ① d개의 고유값과 고유벡터 쌍을 갖는다.
  ② 고유벡터들은 서로 직교한다. (eii⋅ei=0, if ei≠ej)\left(e_{i}{ }_{i} \cdot e_{i}=0, \text { if } e_{i} \neq e_{j}\right)(ei​i​⋅ei​=0, if ei​​=ej​)
  ③ tr⁡(A)=λ1+λ2+λ3+⋯+λd=∑i=1dλi\operatorname{tr}(A)=\lambda_{1}+\lambda_{2}+\lambda_{3}+\cdots+\lambda_{d}=\sum_{i=1}^{d} \lambda_{i}tr(A)=λ1​+λ2​+λ3​+⋯+λd​=∑i=1d​λi​

PCA Procedure

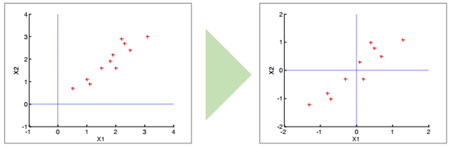
[1] Data Centering

• 평균을 0으로 맞춘다. X′=X−XˉX^{\prime}=X-\bar{X}X′=X−Xˉ 이라고 하면, X′ˉ\bar{X^{\prime}}X′ˉ는 0이 된다.
• 앞서 소개한 Cov⁡(X)=1n(X−Xˉ)(X−Xˉ)T\operatorname{Cov}(X)=\frac{1}{n}(X-\bar{X})(X-\bar{X})^{T}Cov(X)=n1​(X−Xˉ)(X−Xˉ)T의 (X−Xˉ)(X-\bar{X})(X−Xˉ) 과정
• 뒤에서는 식 작성의 편의를 위해 X′=XX^{\prime}=XX′=X로 표기함

[2] Formulation

• 앞에서 만들어진 X(X’)에 대하여 벡터(행렬) X를 기저 w에 정사영 시키면, Cov(X) 식이 다음과 같이 바뀌게 된다.
• 이때 S는 표본 분산의 sample covariance matrix가 된다. ( ∵ 이미 centering 작업을 수행했기 때문에 )

V=1n(wTX)(wTX)T=1nwTXXTw=wTSwV=\frac{1}{n}\left(\mathbf{w}^{\mathrm{T}} \mathbf{X}\right)\left(\mathbf{w}^{\mathrm{T}} \mathbf{X}\right)^{\mathrm{T}}=\frac{1}{n} \mathbf{w}^{\mathrm{T}} \mathbf{X} \mathbf{X}^{\mathrm{T}} \mathbf{w}=\mathbf{w}^{\mathrm{T}} \mathbf{S} \mathbf{w}V=n1​(wTX)(wTX)T=n1​wTXXTw=wTSw

[3] Optimization

• PCA의 목적인 분산을 최대화하는 목적에 따라서 최적화 식은 다음과 같이 나타내질 수 있다.

max⁡wTSw s.t. wTw=1\begin{gathered} \max \mathbf{w}^{\mathrm{T}} \mathbf{S} \mathbf{w} \ \text { s.t. } \mathbf{w}^{\mathrm{T}} \mathbf{w}=1 \end{gathered}maxwTSw s.t. wTw=1​

[4] Solve

• 위에서 구한 최적화식은 바로 풀 수가 없으므로, Lagrange Multiplier(라그랑주 승수법)을 이용하여 풀 수 있다.

💡 여기서 잠깐! Lagrange Multiplier란?
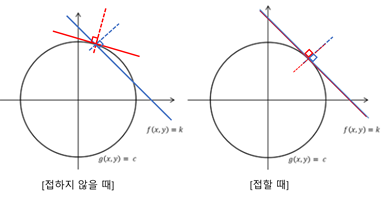
ㅤ라그랑주 승수법 (Lagrange multiplier method)은 기본 가정은 “제약 조건 g(x,y) = c를 만족하는 f(x,y)의 최솟값 또는 최댓값은 f(x,y)와 g(x,y)가 접하는 지점에 존재할 수도 있다.”는 것이다. 이때, f(x,y)와 g(x,y)가 접하는 지점을 찾기 위해 gradient vector(▽)을 이용한다. 어떠한 지점에서 접선 벡터와 gradient vector의 내적은 0이 되게 된다. 따라서, 두 함수 f와 g가 접한다는 것은 두 함수의 gradient vector는 서로 상수배의 관계에 있다고 할 수 있다. 다음 그림을 보면 이를 확인할 수 있다. 이를 식으로 나타내면 다음과 같다: ▽f=λ▽g

ㅤ라그랑주 승수법에서는 다음과 같이 함수를 정의하고, L(x,y,λ)=λ(g(x,y)-c) 로 정의하고, 함수 L의 gradient vector가 영벡터가 되는 점을 찾으면 두 함수 f와 g가 접하게 되는 점을 찾을 수 있게 된다.
ㅤ위에서 정의한 식을 풀어보면, 함수 L의 gradient vector가 영벡터가 되는 점을 찾으면 두 함수 f와 g가 접하는 점을 찾을 수 있다. 함수 L을 x와 y에 대해 편미분하면 총 2개의 식을 얻을 수 있으며, 여기에 제약 조건인 g(x,y)=c를 이용하면 미지수가 3개(x,y,λ)인 문제의 해 (solution)를 구할 수 있다. 여기에서 구한 x와 y는 제약 조건 g를 만족하는 함수 f의 최적점이 될 가능성이 있게 된다.

• 위에서 도출한 maximize 목적함수와 제약식을 이용하여 Lagrange Multiplier(라그랑주 승수법)을 적용하면 다음과 같은 식이 나오게 된다.

  L=wTSw−λ(wTw−1)L=\mathbf{w}^{T} \mathbf{S} \mathbf{w}-\lambda\left(\mathbf{w}^{T} \mathbf{w}-1\right)L=wTSw−λ(wTw−1)

∂L∂w=0⇒Sw−λw=0⇒(S−λI)w=0\frac{\partial L}{\partial \mathbf{w}}=0 \Rightarrow \mathbf{S} \mathbf{w}-\lambda \mathbf{w}=0 \Rightarrow(\mathbf{S}-\lambda \mathbf{I}) \mathbf{w}=0∂w∂L​=0⇒Sw−λw=0⇒(S−λI)w=0

• 결국 주성분 분석의 해는 w는 S의 eigenvector, λ는 S의 eigenvalue 가 된다. 다음은 실제 데이터를 가지고 해당 값을 도출해본 예시이다.

[5] Find the best set of basis

• 분산 계산을 통한 최적의 기저(basis)를 찾을 수 있다.
• 위에서 구한 eigenvalue를 내림차순으로 나열하면 다음과 같이 나타낼 수 있다.

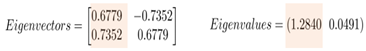
• 이 중 가장 큰 eigenvalue를 λ1, 갖는 eigen vector를 w1이라고 하면, 해당 w1에 projection된 분산량(variation)을 다음과 같이 구할 수 있다.

v=(w1TX)(w1TX)T=w1TXXTw1=w1TSw1\mathbf{v}=\left(\mathbf{w}_{1}^{T} \mathbf{X}\right)\left(\mathbf{w}_{1}^{T} \mathbf{X}\right)^{T}=\mathbf{w}_{1}^{T} \mathbf{X} \mathbf{X}^{T} \mathbf{w}_{1}=\mathbf{w}_{1}^{T} \mathbf{S} \mathbf{w}_{1}v=(w1T​X)(w1T​X)T=w1T​XXTw1​=w1T​Sw1​

Since,ㅤSw1=λ1w1,w1TSw1=w1Tλ1w1=λ1w1Tw1=λ1Since,ㅤ\mathbf{S w}_{1}=\lambda_{1} \mathbf{w}_{1}, \quad \mathbf{w}_{1}^{T} \mathbf{S} \mathbf{w}_{1}=\mathbf{w}_{1}^{T} \lambda_{1} \mathbf{w}_{1}=\lambda_{1} \mathbf{w}_{1}^{T} \mathbf{w}_{1}=\lambda_{1}Since,ㅤSw1​=λ1​w1​,w1T​Sw1​=w1T​λ1​w1​=λ1​w1T​w1​=λ1​

• 따라서, 이렇게 w1에 사영시킨 variation(v)의 값이 λ1인 것을 확인했고, 얼만큼 해당 PC(principal component)가 original variance를 보존하는 가는 다음식을 통해 확인할 수 있다. 이를 통해 해당 주성분은 2차원 데이터를 사영하면 원-데이터의 분산의 96%를 보존한다는 것을 확인할 수 있다.

  λ1λ1+λ2=1.28401.2840+0.0491=0.9632…\frac{λ_{1}}{λ_{1}+λ_{2}}=\frac{1.2840}{1.2840+0.0491}=0.9632…λ1​+λ2​λ1​​=1.2840+0.04911.2840​=0.9632…

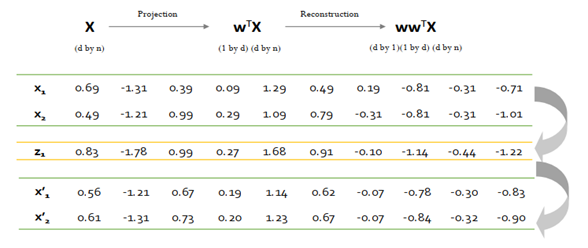
[6] Extraction and Reconstruction

• 주성분(기저)을 이용해 새로운 변수 생성 및 이를 다시 복원할 수 있다.
  (2차원 -> 1차원 -> 2차원)
• 이때, 완벽하게는 복원되지는 않는다. 재구축 오차가 존재하는데, 뒤에 anomaly detection에서 사용할 수 있다.

• 그렇다면 몇 개의 Principal Component(PC)가 최적일까? (정확한 답은 없다ㅠ)
  ① “정성적으로 도메인 전문가가 몇 개가 좋아!”하고 PC의 개수를 정해줄 수 있다.
  ② “정량적으로 원래 변수의 몇 퍼센트가 보존되었는가”를 기준으로 PC의 개수를 정할 수 있다.

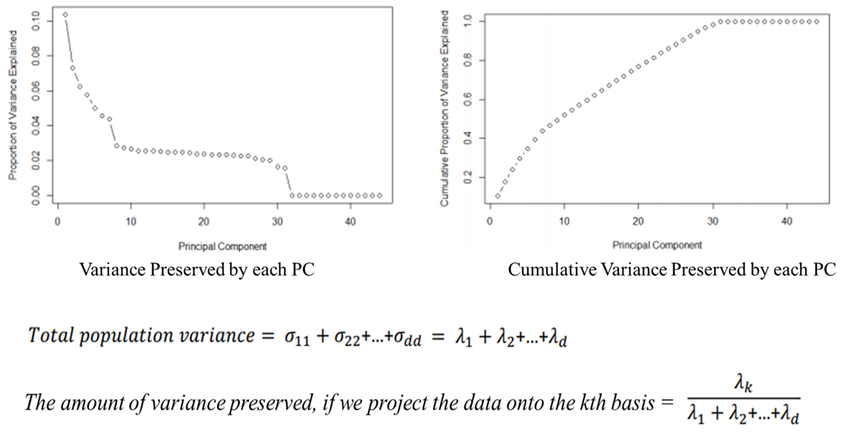
• Scree Plot을 도시화하여, ① 각각의 PC에 대한 variance를 구하여 elbow point(급격하게 감소하는 구간)를 찾거나, ② 누적 설명력 N%기준 설정을 통해 최적의 PC의 개수를 구할 수 있다.

예시를 통해 이해해보자!

PCA가 직관적으로 어떻게 동작하는지 쉽게 이해하기 위해 간단한 예시를 들어보자.

📌 예제: 학생들의 성적 데이터

어떤 학교에서 학생들의 성적 데이터를 분석한다고 가정하자. 데이터는 다음과 같이 여러 개의 과목 점수(국어, 수학, 영어, 과학 등)로 구성되어 있다.

학생	국어	수학	영어	과학
A	90	85	88	92
B	78	75	80	85
C	85	80	82	88
D	70	65	72	78
E	95	90	92	96

이 데이터를 분석해 보면, 과목별 점수들이 서로 어느 정도 상관관계를 가지고 있다는 것을 알 수 있다. 예를 들어, 수학과 과학 점수가 비슷한 패턴을 보이고, 국어와 영어 점수도 유사한 경향을 가진다면, 꼭 4개의 개별 과목 점수(차원)를 모두 사용할 필요가 없을 수도 있다.

📌 PCA 적용

이제 PCA를 적용해 보자.

1️⃣ 데이터 표준화 (Data Centering & Scaling)

• 평균을 0으로 만들고, 분산을 맞춰준다.
• 즉, 과목별 점수 차이를 보정하여 비교할 수 있도록 한다.

2️⃣ 공분산 행렬 계산

• 과목 간의 상관관계를 분석하기 위해 공분산 행렬을 구한다.
• 만약 국어와 영어, 수학과 과학이 강한 양의 상관관계를 가진다면, PCA는 이들을 합쳐 하나의 새로운 축(주성분)으로 표현할 수 있도록 한다.

3️⃣ 고유값(Eigenvalues)과 고유벡터(Eigenvectors) 계산

• PCA는 데이터에서 가장 분산이 큰 방향을 찾아 새로운 기저(Principal Components, 주성분)를 만든다.
• 예를 들어, 첫 번째 주성분(PC1)은 학생들의 전반적인 성적 수준을 나타낼 수 있고, 두 번째 주성분(PC2)은 특정 과목에서의 차이를 강조할 수 있다.

4️⃣ 주성분 선택 및 차원 축소

• 만약 첫 번째 주성분(PC1)이 전체 데이터의 90% 이상의 정보를 설명한다면, 우리는 4개의 과목 점수 대신 하나의 주성분 값만 사용해도 학생들의 성적 패턴을 충분히 분석할 수 있다.

📌 결과 해석

이제 원래 4차원의 데이터를 2차원으로 축소하면 다음과 같은 형태가 될 수 있다.

학생	PC1 (전반적 성적 수준)	PC2 (과목별 편차)
A	1.45	0.12
B	-0.85	0.32
C	0.12	-0.45
D	-1.20	-0.25
E	1.78	0.26

• PC1이 크면 성적이 전반적으로 높음
• PC2는 특정 과목에서의 편차를 반영 (예: 국어 점수는 높은데 수학은 낮은 경우)

이제 우리는 4개의 점수를 다루는 대신, 두 개의 값만 사용하여 학생들의 성적 패턴을 분석할 수 있다. 이는 데이터의 차원을 줄이면서도 중요한 정보를 유지하는 PCA의 핵심 원리와 일치한다.

📖 이렇게 PCA를 적용하면, 원래 4개의 변수(과목 점수)를 모두 다루는 대신 핵심적인 2개의 주성분만으로 데이터를 요약할 수 있다. 이를 통해 데이터 시각화, 클러스터링, 머신러닝 모델링 시 계산량을 줄이면서도 핵심 정보를 유지할 수 있다는 장점이 있다.

PCA Limitation

1. 통계적으로 출발한 모델이기 때문에 가우시안 분포를 가정한다. 그렇기 때문에 가우시안 분포가 아닌 데이터에는 잘 작동되지 않을 수 있다.
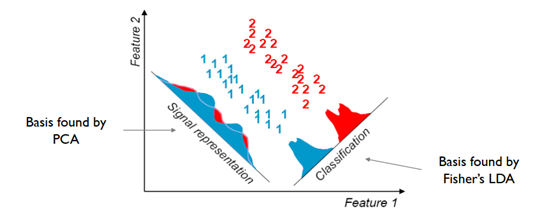
2. 분산을 최대한 보존하는 방식으로 학습을 진행하므로, 분류 모델에는 적당하지 않다.
   (아래 그림 참고)

긴 글 읽어주셔서 감사합니다 ^~^

---

• Previous
  [머신러닝][차원축소] 변수 선택법
• Next
  [머신러닝][시계열] AR, MA, ARMA, ARIMA의 모든 것 - 개념편

---

---

CATALOG

---

FEATURED TAGS

개념정리 OpenAI chatGPT paper-review 환경 Conference 꿀팁 강의노트 python 머신러닝 딥러닝 IT지식 NLP Timeseries git trend-review 이상탐지 CES linux rag vibe coding CIO EXAONE Lovable PyTorch google pandas tools 도서리뷰 Anthropic CV langgraph Claude Conference | SK-AI Distillation Graph 수학 차원축소 AIS IT정리 OLLAMA network pyenv/pipenv snippet

---

FRIEND SITES

• My Velog
• My YouTube
• LGSW YouTube
• DSBA Youtube
• DMQA Youtube