[Paper Review] Visualizing Data using t-SNE

원본 게시글: https://velog.io/@euisuk-chung/Paper-Review-Visualizing-Data-using-t-SNE

선정 이유

오늘 리뷰/번역/구현할 논문은 Visualizing Data using t-SNE으로, 2008년에 Geoffrey Hinton이 저자인 논문입니다. t-SNE(t-Stochastic Nearest Neighbor)은 지금까지도 시각화를 하는 데 자주 사용되는 알고리즘입니다. 이는 고차원의 벡터로 표현되는 데이터 간의 neighbor structure 를 보존하는 2 차원의 embedding vector 를 학습함으로써, 고차원의 데이터를 2 차원으로 표현할 수 있도록 합니다.

논문요약

Abstract

• t-SNE는 2차원 또는 3차원 지도에 가지고 있는 데이터 포인트에 위치를 부여함으로서 이를 시각화할 수 있도록 해주는 방법론입니다.
• t-SNE는 SNE(Stochastic Neighbor Embedding (Hinton and Roweis, 2002)) 방법에서 좀 더 개선된 방법론이며 기존에 있던 crowding problem문제를 해결하기 위해 만들어졌습니다.
• t-SNE는 매우 큰 데이터 세트를 시각화하기 위해 인접 그래프에서 random walks 방법을 사용하여 데이터의 암시적인 구조가 데이터의 하위 집합이 표시되는 방식에 영향을 미치도록 합니다.
• 본 논문에서는 다양한 데이터 세트에서 t-SNE 성능을 보여주고, Sammon Mapping, Isomap 및 locally linear embedding과 비교를 수행합니다.

1. Introduction

• 고차원 데이터의 시각화는 많은 도메인 영역에서 주요하게 다루어집니다.

  • (예시) 유방암 관련 세포 핵(30개의 변수), 이미지 및 문장을 구성하는 벡터들은 몇 백에서 천 개 이상의 변수를 가지고 있습니다.

• 당시 현존하던 아이콘그래픽 디스플레이(iconographic disaplay), Chernoff Face (Chernoff, 1973), pixel-based techniques (Keim, 2000)과 같은 시각화 기법은 대두분 두개 이상의 데이터 차원을 시각화할 수 있도록만 제공해주고, 사람이 이를 해석하는 방식으로 진행이 되었습니다.

  

  Chernoff-face : https://en.wikipedia.org/wiki/Chernoff_face

pixel-based techniques : https://www.semanticscholar.org/paper/Pixel-Oriented-Visualization-Techniques-for-Very-Keim/ce1eb9ed41232690a1ab0b6b7322cfdb10a385cc

• 이와는 반대로, 차원축소(dimensional reduction) 방법은 고차원 데이터를 저차원(2차원 또는 3차원)으로 축약시켜, 이를 산점도로 표현을 해줄 수 있게 합니다.

• 차원 축소의 목표는 저차원 데이터에서 중요한 고차원데이터의 구조를 유지해주는 것입니다.

  X=[x1,x2,…,xn]→Y=[y1,y2,…,yn]X = [x_{1},x_{2}, … ,x_{n}] → Y= [y_{1},y_{2}, … ,y_{n}]X=[x1​,x2​,…,xn​]→Y=[y1​,y2​,…,yn​]

• PCA(주성분분석), MDS(다차원척도법)은 대표적인 차원축소 방법론으로, 서로 다른 데이터 포인트의 저차원 표현으로 멀리 떨어뜨리는 데 초점을 맞춘 선형 기술입니다.

• 고차원 데이터에서는 선형 매핑으로는 고차원 데이터 정보유지가 불가능하여 데이터의 지역 구조를 보존하는 것을 목표로 하는 많은 수의 비선형 차원 감소 기술이 제안되었습니다.

  • Sammon Mapping (Sammon, 1969)
  • Curvilinear Components Analysis (CCA; Demartines and Herault, 1997)
  • Stochastic Neighbor Embedding (SNE, Hinton and Roweis , 2002)
  • Isomap (Tenenbaum et al., 2000)
  • Maximum Variance Unfolding (MVU; Weinberger et al., 2004)
  • Locally Linear Embedding (LLE; Roweis and Saul, 2000)
  • Laplacian Eigenmaps (Belkin and Niyogi, 2002).
• 하지만, 이러한 방법론들도 고차원 데이터의 로컬 또는 글로벌한 정보를 둘 다 잘 유지하지는 못하였다. t-SNE는 이를 가능하게 해줍니다.

1. Stochastic Neighbor Embedding

• SNE(Stochastic Neighbor Embedding)은 데이터 점 사이의 고차원의 “유클리드 거리”를 “유사성을 나타내는 조건부 확률”로 변환하여 사용합니다.

• SNE는 pj∣ip_{j

  i}pj∣i​와 qj∣iq_{j

  i}qj∣i​사이의 불일치를 최소화하는 저차원 데이터 표현을 찾는 것을 목표로 합니다.

• pj∣ip_{j

  i}pj∣i​ 는 고차원 데이터 포인트의 조건부, qj∣iq_{j

  i}qj∣i​ 는 저차원 데이터 포인트의 조건부입니다

  • xjx_{j}xj​와 xix_{i}xi​의 유사성은, xix_{i}xi​가 xix_{i}xi​를 중심으로 한 가우스 아래에서 확률 밀도에 비례하여 이웃을 선택한다면 xjx_{j}xj​를 이웃으로 선택할 수 있는 조건부 확률 pj∣ip_{j

    i}pj∣i​를 의미합니다.

    pj∣i=exp(−∣xi−xj∣2/2σi2)∑k≠iexp(−∣xi−xk∣2/2σi2)p_{j

    i}=\frac{exp(−

    x_{i}−x_{j}

    ^{2}/2σ^{2}_{i})}{∑_{k≠i}exp(−

    x_{i}−x_{k}

    ^{2}/2σ^{2}_{i})}pj∣i​=∑k​=i​exp(−∣xi​−xk​∣2/2σi2​)exp(−∣xi​−xj​∣2/2σi2​)​

  • yjy_{j}yj​와 yiy_{i}yi​의 유사성은, yiy_{i}yi​가 yiy_{i}yi​를 중심으로 한 가우스 아래에서 확률 밀도에 비례하여 이웃을 선택한다면 yjy_{j}yj​를 이웃으로 선택할 수 있는 조건부 확률 qj∣iq_{j

    i}qj∣i​를 의미합니다.

    qj∣i=exp(−∣yi−yj∣2)∑k≠iexp(−∣yi−yk∣2)q_{j

    i}=\frac{exp(−

    y_{i}−y_{j}

    ^{2})}{∑_{k≠i}exp(−

    y_{i}−y_{k}

    ^{2})}qj∣i​=∑k​=i​exp(−∣yi​−yk​∣2)exp(−∣yi​−yj​∣2)​

  • 조건부 확률 값(pj∣ip_{j

    i}pj∣i​)이 높으면 데이터 포인트가 가깝습니다.

  • 조건부 확률 값(pj∣ip_{j

    i}pj∣i​)이 낮으면 데이터 포인트가 멉니다.

  • pi∣i=0p_{i

    i}=0pi∣i​=0 , qi∣i=0q_{i

    i}=0qi∣i​=0 ,

  • SNE는 가우시안 분포를 따르기 때문에, 인접 데이터 포인트의 경우 조건부 확률이 높지만, 넓게 분리된 데이터 포인트의 경우 조건부 확률이 발산하게 됩니다.
• 차원 축소가 제대로 잘 이뤄졌다면 고차원 공간에서 이웃으로 뽑힐 확률과 저차원 공간에서 이웃으로 뽑힐 확률이 비슷할 것입니다. 이렇듯 SNE의 목적은 p와 q의 분포 차이가 최대한 작게끔 하고자 합니다.

• 두 확률분포가 얼마나 비슷한지 측정하는 지표 척도는 Kullback-Leibler divergence를 이용합니다.

  • KL Divergence는 어떤 확률 분포를 다른 확률 분포로 근사할 때 정확히 얼마나 많은 정보(엔트로피)가 손실되는지를 계산할 수 있습니다.
  • 두 확률분포가 완전히 다르면 1, 동일하면 0의 값을 갖습니다.

  • SNE는 아래 비용함수를 최소화하는 방향으로 학습을 진행하게 됩니다.

    Cost=∑iKL(Pi∣Qi)=∑i∑jpj∣ilogpj∣iqj∣iCost = ∑_{i}KL(P_{i}

    Q_{i}) = ∑_{i}∑_{j}p_{j

    i}log\frac{p_{j

    i}}{q_{j

    i}}Cost=∑i​KL(Pi​∣Qi​)=∑i​∑j​pj∣i​logqj∣i​pj∣i​​

• SNE 비용 함수는 맵에서 데이터의 로컬 구조를 유지하는데 초점을 맞춥니다.
• 선택될 나머지 파라미터는 각각의 고차원 데이터 포인트 xi에 집중되는 가우시안의 분산 σi의 단일 값으로 하는 것은 부적절합니다. (데이터의 밀도가 다양하기 때문에, 밀도가 높은 영역에서 σi의 값이 작을수록 좋음)
• 어떤한 σi 값이던 다른 모든 데이터 포인트에 대해 확률분포 Pi를 유도됩니다. 분포는 σi가 증가함에 따라 증가하는 엔트로피를 갖습니다.

• SNE는 σi의 값에 대해 이진 검색을 수행합니다. 사용자가 지정한 고정된 복잡도(perplexity)를 갖는 Pi를 생성합니다. Perplexity는 다음과 같이 정의됩니다.

  Perp(Pi)=2H(Pi)Perp(P_{i}) = 2^{H(P_{i})}Perp(Pi​)=2H(Pi​)

• 이때 H(Pi)H(P_{i})H(Pi​)는 Shannon Entrophy of PiP_{i}Pi​입니다.

  H(Pi)=−∑jpj∣ilog2pj∣iH(P_{i}) = -∑_{j}p_{j

  i}log_{2}p_{j

  i}H(Pi​)=−∑j​pj∣i​log2​pj∣i​

• SNE의 값은 perplextity에 큰 영향을 받지 않습니다. (fairly robust)
• 최종적으로 구하고자 하는 미지수는 저차원에 임베딩된 좌표값 yi, SNE는 그래디언트 디센트(gradient descent) 방식으로 yi들을 업데이트합니다.

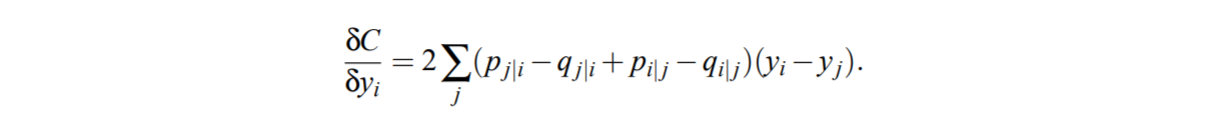
• 최적화 초기에는 가우시안 노이즈를 추가하여 local minimum 에 빠지지 않도록 유의한다. 하지만 이러한 과정이 한번에 이뤄질 수는 없습니다. 적당한 amount of momentum과 step size를 찾기 위해 여러번 반복 수행을 해주어야 합니다.

1. t-Distributed Stochastic Neighbor Embedding

3.1. Symmetric SNE

• 앞에서 정의한 거리 함수는 조건부 확률이기 때문에 Symmetric(비대칭)하지 못하므로, 데이터 쌍에 대한 Joint Probability(대칭)을 사용하였습니다.

• 이전 조건부확률, 사건 B가 발생했다는 가정하에 사건 A가 일어날 확률 ( pj∣ip_{j

  i}pj∣i​≠pi∣jp_{i

  j}pi∣j​ )

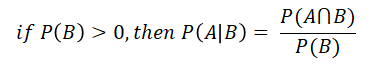
• Joint Probability란, 두개의 서로다른 사건 A, B가 동시에 일어날 확률 ( p(j,i)p(j,i)p(j,i) = p(i,j)p(i,j)p(i,j) )

• Joint Probability를 사용해줌으로서 연산이 빨라질 수 있었습니다.
• 대칭 SNE의 gradient는 비대칭 SNE의 gradient와 상당히 유사하며 실험에서 대칭 SNE가 비대칭 SNE와 마찬가지로 좋고 경우에 따라 조금 더 나은 맵을 생성하는 것으로 나타났습니다.
• σi는 각 개체마다 데이터 밀도가 달라서 이웃으로 뽑힐 확률이 왜곡되는 현상을 방지하기 위한 값입니다. 저자는 반복 실험 결과 p를 계산할 때 쓰는 σi는 고정된 값을 써도 성능에 큰 차이를 보이지 않았다고 하여 σi 계산을 생략하였습니다.

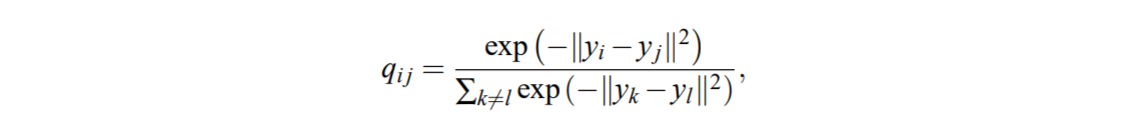
• 대칭점 간의 유사도를 대칭적으로 만들기 위하여 두 확률 값의 평균으로 두 점간의 유사도를 정의해주었습니다.

• 변경된 수식의 Cost Function과 그 gradient 값은 다음과 같습니다.

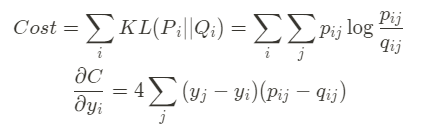
3.2. The Crowding Problem

• 고차원에서 저차원으로 점을 Projection 하면, 거리가 멀고 가까운 개념이 붕괴되는 경우가 있습니다. 3차원에서는 서로 다른 4개의 점이 서로와 같은 거리에 위치하도록 할 수 있는데 2차원에서는 4개의 점이 거리가 달라지게 됩니다. (The Crowding Problem)
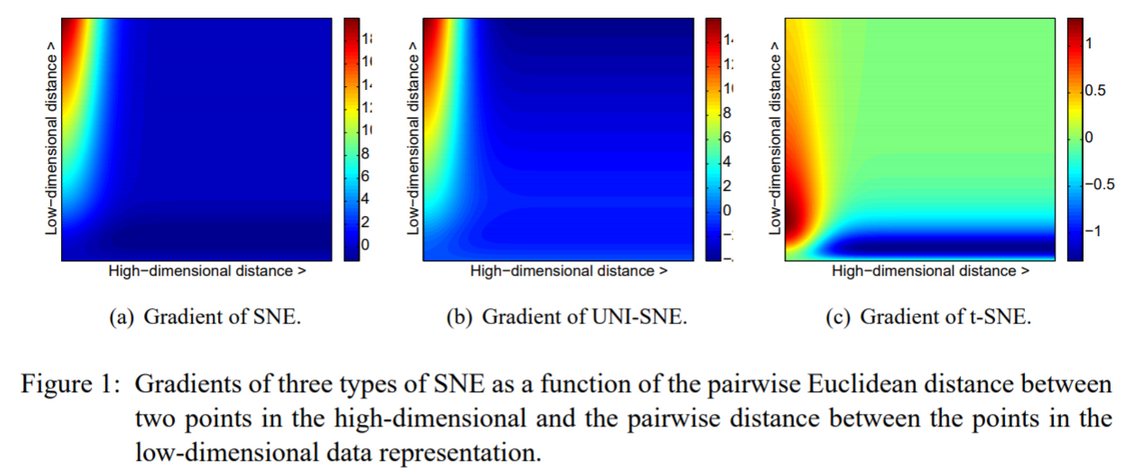
• t-SNE 전에 제안된 방법으로 UNI-SNE가 있습니다. 모든 스프링에 약간의 거부감을 더함으로써 혼잡 문제를 해결하려는 시도가 제시되었습니다. (2007, Cook et al).
• 고차원에서 멀리 떨어져 있던 점은 저차원에서 더 멀게, 고차원에서 가까웠던 점은 저차원에서 더 가깝게 만들어줄 인위적인 장치가 필요하여 고안된 방법이 바로, Student t-Distribution입니다.
• Low Dimensional Domain에서만 Gaussian 대신에 수정된 형태(Student t-Distribution)의 분포를 사용하고, High Dimensional에서는 이전과 마찬가지로 가우시안 분포 사용하게 합니다.

source : https://andyjconnelly.wordpress.com/2017/05/16/uncertainty-and-repeats/

3.3. Mismatched Tails can Compensate for Mismatched Dimensionalities

• t-SNE에서는 저차원 지도에 있는 heavy-tailed 분포로서 자유도가 1도인 학생 t-분포를 채용하고 있습니다(Cauchy 분포와 동일). 이 분포를 사용하여 공동 확률 qijq_{ij}qij​를 다음과 같이 정의합니다.

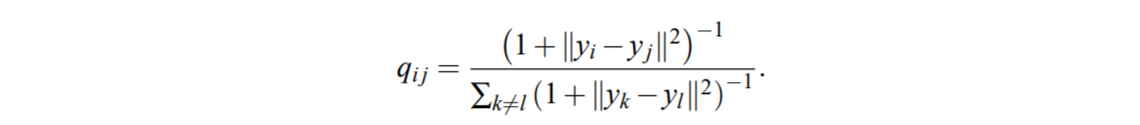
• 계산적으로 편리한 속성은 Student t 분포가 Gaussians의 무한한 혼합(infinite mixture of Gaussians)과 같음에도 불구하고 지수가 포함되지 않기 때문에 Student t 분포 아래의 점의 밀도를 가우시안보다 더 빠르게 평가합니다.
• The gradient of the Kullback-Leibler divergence between P and the Student-t based joint probability distribution Q

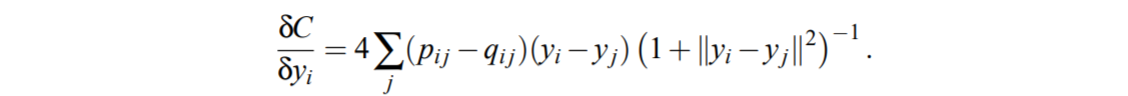
source : 논문 원문

• 저자는 t-SNE가 기존 SNE와 UNI-SNE에 비하여 좋은 이유로 2가지 이유를 듭니다.

1. t-SNE 그라디언트는 저차원 표현에서 작은 pairwise distance로 모델링 된 다른 datapoints를 강하게 반발합니다.
2. t-SNE가 작은 pairwise distance에 의해 모델링된 다른 datapoint들 사이에 일으킨 강력한 반발은 무한대로 발산하지 않습니다.

• 요약하자면, t-SNE는 (1) 큰 pairwise 거리를 사용하여 서로 다른 datapoints를 모델링하고, (2) 작은 pairwise 거리를 사용하여 유사한 datapoints를 모델링하는 데 중점을 둡니다.

3.4. Optimization Methods for t-SNE

• 다음은 해당 논문이 제시한 t-SNE 알고리즘입니다.

source : 논문 원문

• 위 알고리즘에 나온 공식들을 정리해보자면 다음과 같습니다.

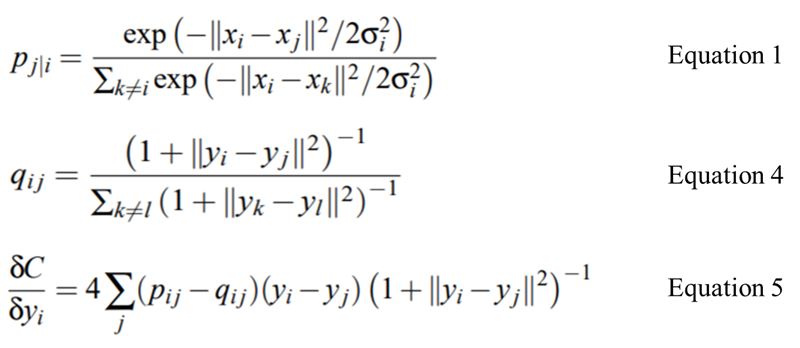
• gradient decent를 진행하면 불안정하기 때문에 momentum으로 paraemter를 업데이트합니다. 반복 횟수를 줄이기 위해 momentum을 활용하며, momentum이 작으면 맵 포인트가 적절하게 잘 정리 될 때까지 학습이 됩니다.
• Jacobs(1988)에 의해 설명된 adaptive learning rate를 사용하여 학습을 가속화 할 수 있는데, 이 방법은 그라디언트가 안정한 방향으로 점진적으로 학습 속도를 증가시킵니다.
• 알고리즘이 다른 비모수 차원의 축소 기술로 생성된 것보다 훨씬 나은 시각화를 생성하지만, 아래의 2가지 효과적인 방법을 통해 좀 더 효율적으로 최적화를 수행할 수 있습니다.

1. Early Compression (이른 압축 방법)

   • 최적화가 시작될 때 맵 포인트들이 서로 가까이에 있도록 강제합니다. (force the map points to stay close together at the start of the optimization)
   • 맵 포인트 사이의 거리가 작으면 클러스터가 서로 이동하기 쉽기 때문에 가능한 글로벌 하게 데이터의 공간을 탐색하는 것이 훨씬 쉬워집니다.
   • 원점으로부터의 맵 포인트의 제곱 거리의 합에 비례하는 비용 함수에 L2 페널티를 추가함으로써, 페널티 기간의 크기와 반복은 수동으로 설정해줍니다.

2. Early Exaggeration (이른 과장 방법)

   • pij에 특정 상수(논문 예시로 4)를 곱하여, qij가 상대적으로 작기 때문에 pij에 대응하기 위하여 크게 움직이고 맵 포인트가 넓게 움직이도록 합니다.
   • 클러스터가 맵 포인트에서 단단하고 서로 간의 넓게 분리된 클러스터를 형성하는 경향으로 빈 공간이 많이 생길 수 있도록 조정해주는 데 의의가 있습니다.

3. Experiments

• t-SNE를 평가하기 위해, 차원 축소를 위한 7가지 다른 비모수 기술과 비교되는 실험을 제시합니다.
• 본 논문에서는 (1) Sammon 매핑, (2) Isomap, (3) LLE 만 t-SNE와 비교합니다.
• Appendix에서 t-SNE와 CCA, (5) SNE, (6) MVU 및 (7) Laplacian 고유 맵을 비교합니다. (본 포스트에서는 생략)

4.1. Data Sets

실험으로 아래 5개의 데이터 세트를 이용했습니다:

1. MNIST 데이터 세트
2. Olivettifaces 데이터 세트
3. COIL-20 데이터 세트
4. the word-features 데이터 세트
5. Netflix 데이터 세트

4.2. Experimental Setup

• 모든 실험에서 데이터의 차원을 30으로 줄이기 위해 PCA를 사용했습니다. 이렇게 해주면, 데이터 포인트 간의 pairwise 거리 계산 속도가 빨라지고 interpoint 거리가 심각하게 왜곡되지 않고 일부 노이즈가 억제됩니다.
• 차원축소 기술을 사용하여 30 차원 표현을 2 차원 지도로 변환하여 결과 맵을 산점도로 표시해줍니다.
• 모든 데이터 세트에 대해 각 데이터 포인트의 클래스에 대한 정보가 있지만 클래스 정보는 맵 포인트의 색상(or 심볼)을 선택하는 데만 사용되었습니다. (클래스 정보는 맵 포인트의 공간 좌표를 결정하는 데 사용되지 않음)
• Table 1에서 Perp(perplexity)는 가우시안 커널에 의해 유도된 조건부 확률 분포의 복잡도를 나타내고, k는 인접 그래프에 사용된 가장 가까운 이웃의 수를 나타냅니다.

Source : 논문 본문

• Isomap과 LLE을 사용한 실험에서, 오직 대응하는 데이터 포인트만 시각화를 수행하였습니다.
• Sammon 매핑 최적화의 경우, Newton 방법을 수행하였습니다. (iter =500)

4.3. Results

Source : 논문 본문

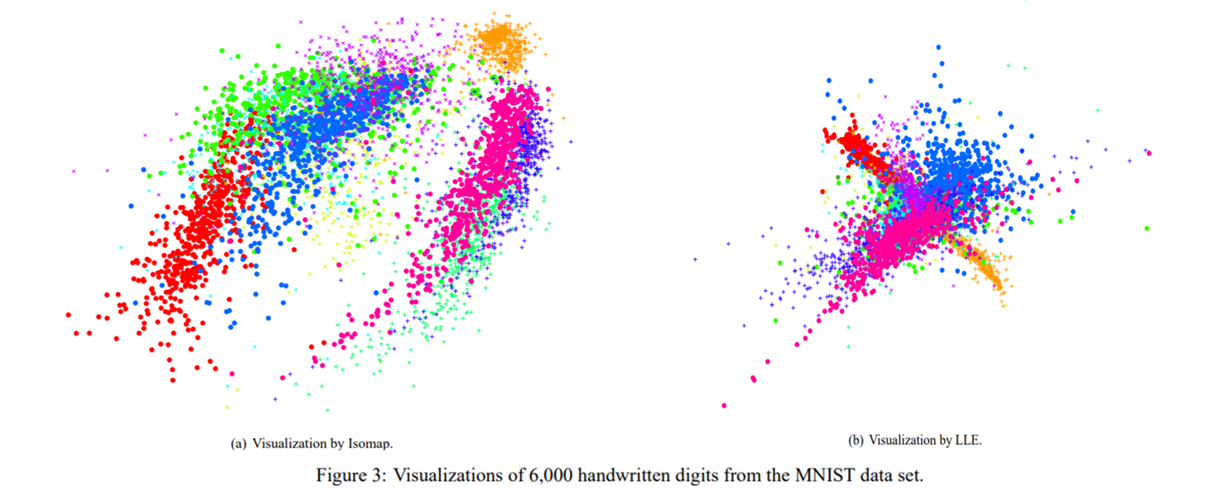
• Figure 2와 Figure 3에서 MNIST 데이터 세트에서 t-SNE, Sammon 매핑, Isomap 및 LLE을 사용한 실험 결과를 보여줍니다.
• 해당 결과는 다른 기술에 비해 t-SNE의 강력한 성능을 보여줍니다. t-SNE는 숫자 클래스들 사이의 분리가 거의 완벽한 맵을 구성합니다.
• Sammon 매핑은 3 개의 클래스 (숫자 0, 1 및 7을 나타내는)만 다른 클래스와 약간 분리 된 “공” 형태로 만듭니다.
• Isomap과 LLE는 숫자 클래스 사이에 큰 중복이 있는 솔루션을 생성합니다.
• t-SNE 맵의 상세한 검사는 데이터의 국부적인 구조 (예를 들어, 방향)가 캡쳐되는 것을 확인할 수 있습니다.

Source : 논문 본문

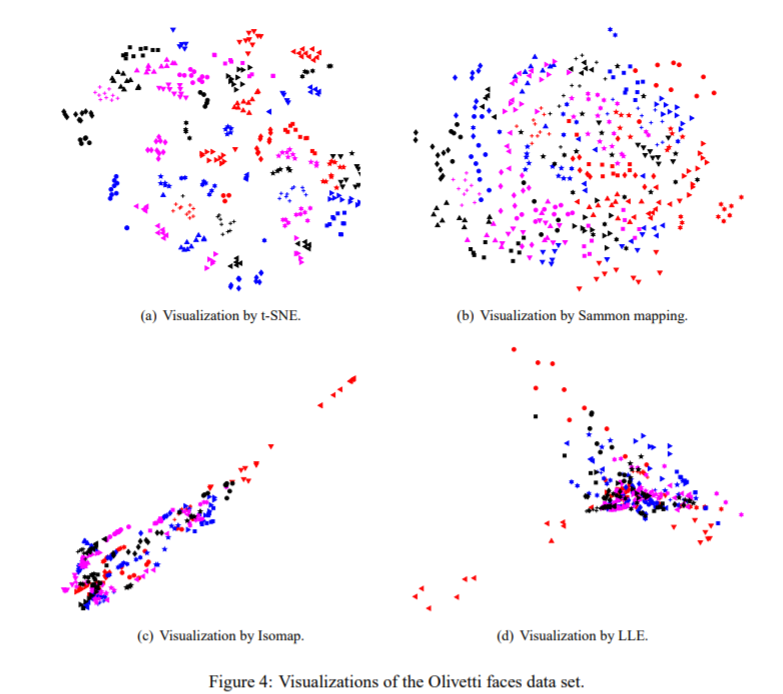
• Figure 4는 t-SNE, Sammon 매핑, Isomap 및 LLE를 Olivetti 얼굴 데이터 세트에 적용한 결과입니다.
• t-SNE는 데이터의 자연스러운 클래스를 잘 들어내 주었습니다. 예를 들어 어떤 사람들의 10 개의 이미지가 두 개의 cluster로 나뉘는 등의 성능을 보입니다. 보통 이미지의 하위 집합이 머리가 크게 다른 방향을 향하고 있기 때문에, 또는 매우 다른 표현이나 안경을 가지고 있기 때문에 다른 cluster로 인식하였습니다.
• Isomap과 LLE는 데이터의 클래스 구조에 대해 거의 통찰력을 제공하지 못하는 솔루션을 제공하였습니다.
• Sammon 맵핑에 의해 생성된 맵은 각 클래스의 멤버 중 상당수를 서로 가깝게 모델링했기 때문에 isomap이나 LLE보다는 좋았지만, 어떤 클래스도 맵 상에서는 명확히 분리되어 있지 않았습니다.
• Olivetti 얼굴 이미지에서 픽셀 공간에서 유클리드 거리를 사용할 때 1명당 10 개의 이미지가 자연스러운 클래스를 형성한다는 것이 명확하지 않습니다.

Source : 논문 본문

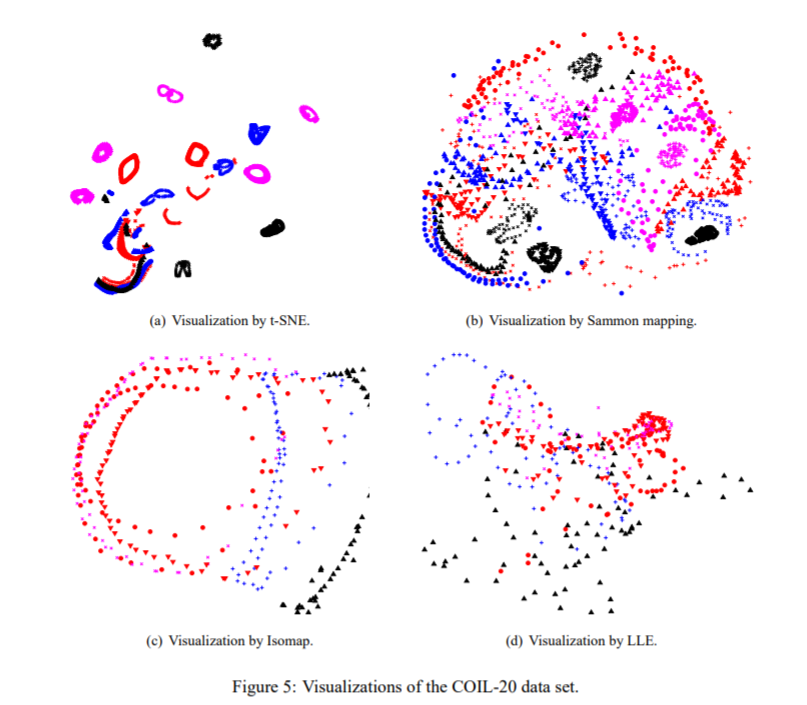
• Figure 5는 t-SNE, Sammon 매핑, Isomap 및 LLE을 COIL20 데이터 세트에 적용한 결과입니다.
• 20 개의 객체 중 많은 부분에서 t-SNE은 닫힌 루프와 같이 1 차원 관점의 다양성을 정확하게 나타내는 것을 확인할 수 있습니다. 앞면과 뒷면에서 비슷하게 보이는 물체의 경우, t-SNE가 루프를 왜곡하여 앞면과 뒷면의 이미지가 가까운 지점에 매핑됩니다. COIL-20 데이터 세트에 있는 4 가지 유형 (four manifolds)를 명확히 구분해냅니다.
• 하지만 t-SNE를 제외한 나머지 3개의 방법론들은 이를 명확하게 분리해내지 못 합니다. Figure 5는 또한 다른 세 가지 기술이 매우 다른 대상에 해당하는 매니 폴드를 깨끗하게 분리하는 것과 거의 비슷하지 않음을 보여줍니다.
• 또한 Isomap과 LLE는 COIL-20 데이터 세트에서 소수의 클래스만 시각화합니다.

1. Applying t-SNE to Large Data Sets

• 다른 많은 시각화 기술과 마찬가지로 t-SNE는 quadratic in the number of datapoints를 계산하는데는 메모리 복잡성이 있습니다. t-SNE의 표준 버전을 10,000 포인트 이상을 포함하는 데이터 세트에 적용하는 것은 실행 불가능합니다.

Source : 논문 본문

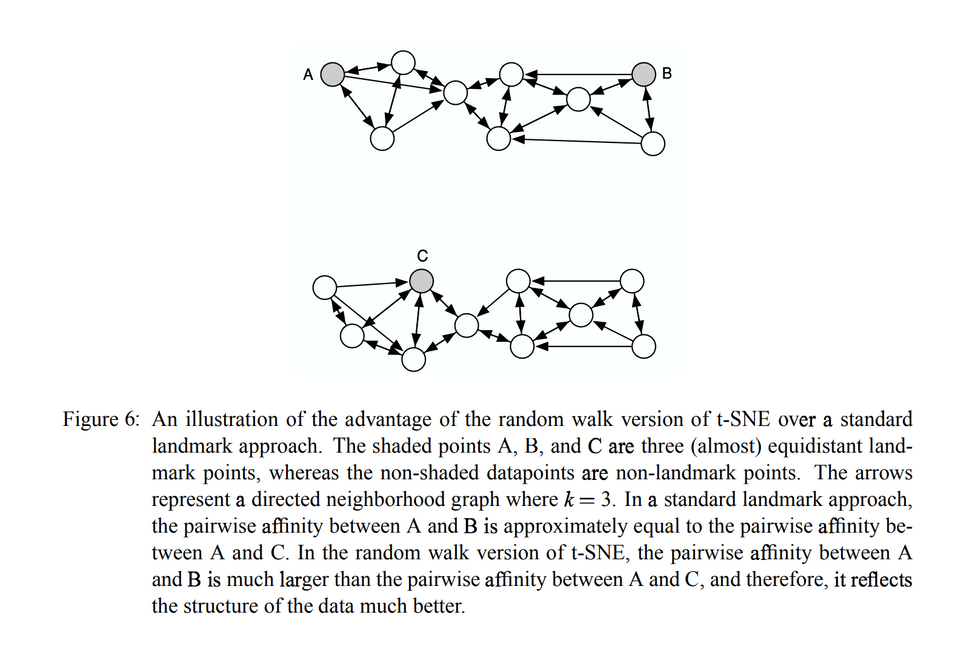
• 이번 파트에서는 전체(대략적으로 매우 큰) 데이터 집합의 정보를 사용하는 방식으로 t-SNE를 수정하여 데이터 점(일명 landmark point)의 랜덤 서브셋을 표시하는 방법을 보여줍니다. 매우 큰 데이터 세트의 정보를 사용하는 방식으로 데이터 포인트의 랜덤 서브 세트를 표시하도록 t-SNE를 수정하는 방법을 제안합니다. (Figure 6 참고)

• 표시되지 않은 데이터 포인트가 기본 매니폴드에 대해 제공하는 정보를 사용합니다. 밑에 예시를 보도록 하겠습니다.

  • A, B, C가 모두 고차원 공간에서 등거리에 있다고 가정하겠습니다.
  • A와 B 사이에 많은 표시되지 않은 데이터 포인트가 있고 A와 C 사이에 없는 데이터 포인트가 많으면 A와 B가 A와 C와 동일한 클러스터의 일부가 될 확률이 더 높습니다.

• 해당 방법론은 다음과 같은 순서를 따릅니다.

  • 원하는 이웃 수를 선택하고 모든 데이터 포인트에 대해 인접 그래프를 만듭니다. 연산량이 많지만 필요한 과정이기에 한 번만 수행합니다.
  • 각 랜드마크 포인트에 대해, 랜드마크 포인트에서 시작하여 다른 랜드마크 포인트에 도착하자마자 새로운 랜덤 워크를 정의합니다.

  • 랜덤워크를 수행하는 동안, 노드 xi에서 노드 xj로 발산하는 에지를 선택할 확률은 e−∣xi−xj∣2e^{-

    x_{i}-x_{j}

    ^{2}}e−∣xi​−xj​∣2에 비례합니다.

  • pj∣ip_{j

    i}pj∣i​를 랜드마크 포인트 xi에서 시작하여 랜드마크 포인트 xj에서 끝나는 무작위 도보의 비율로 정의합니다.

• 이 방법은 Isomap이 점 사이의 쌍 방향 거리를 측정하는 방식과 닮았지만, diffusion map (Lafon and Lee, 2006; Nadler et al., 2006)에서와 같이 가장 짧은 인접(shortest path)만을 보는 게 아니라, 이를 활용해 랜덤 워크 기반의 측정치가 인접 그래프를 통해 모든 경로에 통합되도록 하여 결과적으로 무작위 워크 기반 측정은 short-circuit (Lee and Verleysen, 2005)에 훨씬 덜 민감합니다.

• 랜덤 워크 기반 유사도(pj∣ip_{j

  i}pj∣i​)를 계산하는 가장 확실한 방법은 100만번의 랜덤 워크를 쉽게 수행할 수 있다는 것을 감안할때, 이를 명시적으로 수행하는 것입니다.

• 또는 Grady (2006)는 sparse 선형 시스템을 해결하는 쌍 방향 유사도 를 계산하는 분석 솔루션을 제시하기도 하였습니다. (예비 실험에서 Random Walk(무작위 걸음)를 명시적으로 수행하는 것과 분석적 솔루션 사이에 큰 차이점을 발견하지 못함)

Source : 논문 본문

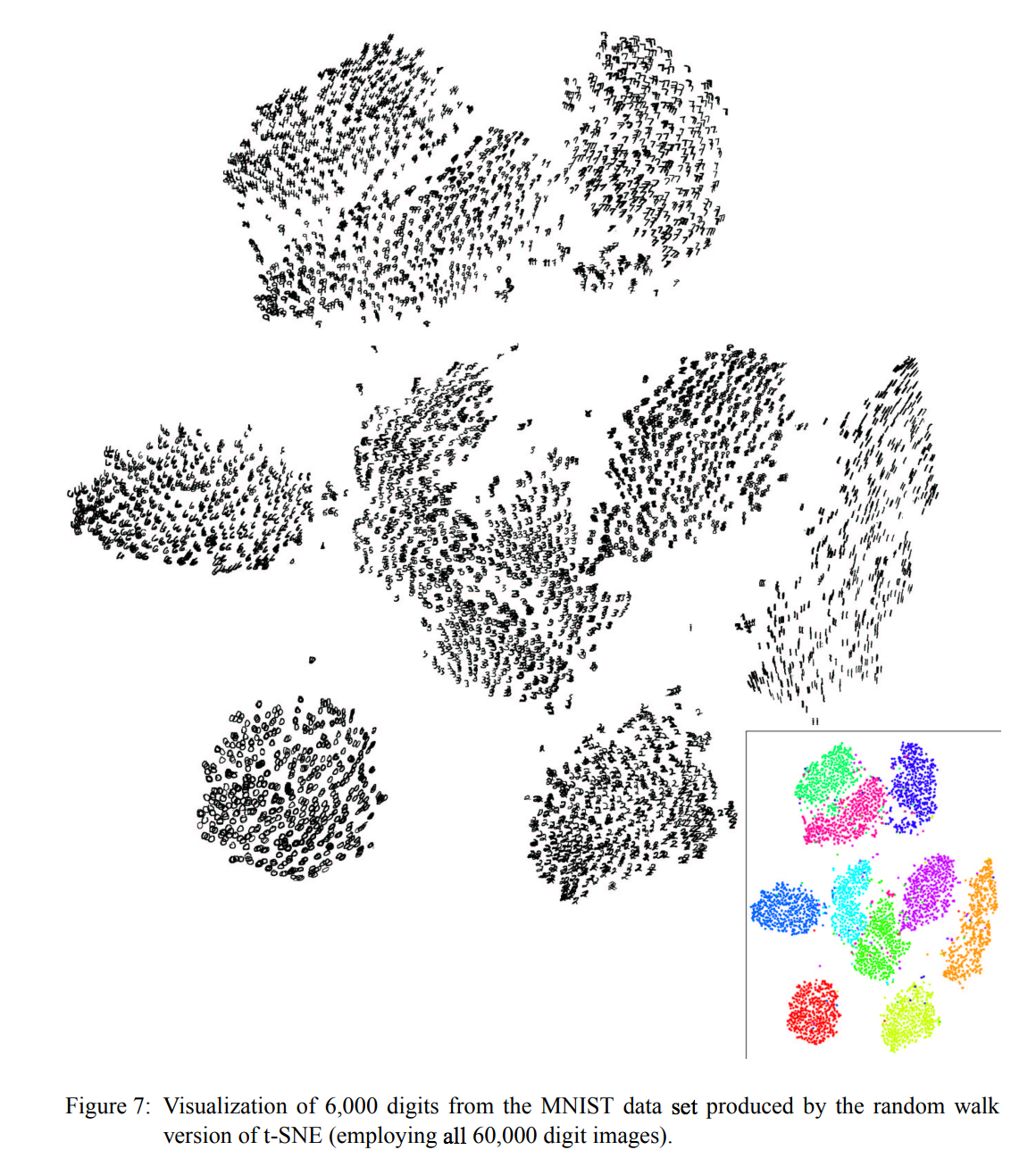
• Figure 7은 랜덤 워크 버전을 적용한 실험 결과로, t-SNE를 MNIST 데이터 세트(60,000 숫자)로부터 무작위로 선택된 6000개를 이용하여 pairwise 유사성 pj∣ip_{j

  i}pj∣i​를 계산한 것입니다. 실험에서는 k = 20 가까운 이웃들의 값을 사용하여 구성된 이웃 그래프를 사용하였습니다.

• 삽입 그림(inset figure)은 색상이 자릿수의 레이블을 나타내는 산점도와 동일한 시각화를 나타냅니다.
• t-SNE 맵에서는 모든 클래스가 명확하게 구분됩니다. 또한, t-SNE는 1, 4, 7, 9의 방향이나 2의 “고리 모양”과 같은 각 클래스 내의 변형의 주 크기를 나타냅니다.
• t-SNE의 강한 성능은 또한 저차원 표현에 대해 훈련된 가장 가까운 이웃 분류 자의 일반화 오차에 반영합니다.
• 원래의 784 차원 데이터 점에 대해 훈련된 최근접 이웃 분류기의 일반화 오차 (10 배 교차 검증을 사용하여 측정)가 5.75 % 인 반면에, 2 차원에 훈련 된 최근접 이웃 분류기의 일반화 오차 t-SNE에 의해 생성된 데이터 표현은 단지 5.13 %에 불과하게 됩니다.

1. Discussion

앞의 두 섹션에서 다양한 데이터 세트에서 t-SNE의 성능을 보였습니다. 이 섹션에서는 t-SNE와 다른 비모수 기법의 차이점에 대해 논의하고, 약점 및 가능한 개선점을 논의합니다.

6.1. Comparison with Related Techniques

• PCA 와 밀접한 관계가 있는 classical scaling(Torgerson, 1952)은 고차원적 쌍 거리와 그것들 사이의 제곱 오차의 합을 최소화하는 데이터의 선형 변환을 발견하였습니다.

  • Classical scaling과 같은 선형 방법은 근처의 데이터 점 사이의 거리를 유지하는 것이 아니라 널리 분리 된 데이터 점 사이의 거리를 유지하는 데 초점을 맞추었습니다. 하지만, 이는 곡선 매니 폴드를 모델링하는데 좋지 않습니다.

• Classical scaling의 문제를 해결하기위한 중요한 접근 방법으로 제시된 것이 바로 Sammon 매핑 (Sammon, 1969)입니다.

  • 이 방법은 각각의 pairwise 유클리드 거리의 표현에서 제곱 오차를 높은 유클리드 거리로 나누어 classical scaling의 비용 함수를 변경해줍니다.

  1
  2
  3
  4
  5
  	![Cost Func](https://velog.velcdn.com/images%2Feuisuk-chung%2Fpost%2F2c2e78ec-c91d-4c0d-b6c5-b7ddfa3b1873%2Fimage.png)
    
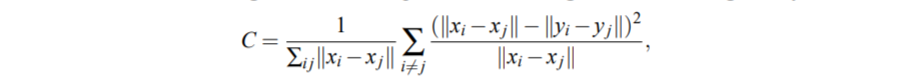  	- 결과 비용 함수는 그레디언트의 유도를 단순화하기 위해 합계 외부의 상수가 추가되는 위치에 의해 제공됩니다.
  	- Sammon 비용 함수의 가장 큰 약점은 지도에서 쌍거리를 유지하는 중요성이 pairwise 거리의 작은 차이에 크게 의존한다는 점입니다.
  	- 작은 pairwise 거리가 데이터의 로컬 구조를 고려할 때 작은 쌍 거리에 거의 동일한 중요성을 부여하는 것이 더 적합합니다. 특히, 매우 근접한 2 개의 고차원 점 모델의 작은 오차는 비용 함수에 큰 기여를 합니다.
  

• Sammon 매핑과는 달리, t-SNE에 의한 고차원 공간에서 사용된 가우시안 커널은 데이터의 로컬 및 글로벌 구조와 가우스의 표준 편차에 비례하여 서로 가까운 데이터 점 쌍에 대한 소프트 경계를 정의하게 됩니다.

  • 분리를 모델링하는 것의 중요성은 분리의 크기와 거의 무관합니다.

  • t-SNE는 데이터의 로컬 밀도에 기초하여 각 데이터 포인트에 대한 로컬 인접 크기를 개별적으로 결정합니다.

• Isomap에 비해 t-SNE가 강력한 이유 : Isomap의 “short-circuiting”에 대한 취약성 + Isomap은 주로 작은 측지 거리보다는 큰 측지선 거리를 모델링하는 데 중점을 두기 때문입니다.
• LLE에 비해 t-SNE가 강력한 이유 : LLE는 기본적으로 모든 데이터 포인트가 단일 지점으로 접히는 것을 방지하기 위해 저 차원 표현의 공분산에 대한 제약을 둡니다. 실제로 이 제약 조건은 대다수의 맵 포인트를 맵의 중앙에 배치하고 몇 개의 널리 분산 된 포인트를 사용하여 큰 공분산을 만듭니다.
• 또한 Isomap 및 LLE와 같은 인접 그래프 기반 기술은 두 개 이상의 널리 분리 된 하위 매니 폴드로 구성된 데이터를 시각화 할 수 없습니다. 이러한 데이터는 연결된 인접 그래프를 발생시키지 않기 때문입니다. 연결된 각 구성 요소에 대해 별도의 지도를 생성 할 수도 있지만 이 방법은 상대적 유사성에 대한 정보를 잃어버리게 됩니다.

6.2. Weaknesses

• t- SNE는 데이터 시각화를 위한 다른 기술과 비교하여 유리하지만, tSNE는 세 가지 잠재적인 약점을 갖습니다.

  1. t-SNE이 일반적인 차원 축소 작업에서 분명하지 않습니다.

  2. t-SNE는 차원의 저주에 민감합니다.

  3. t-SNE의 비용 함수가 전역 최적값으로 수렴된다는 보장이 없습니다.

1. 약점 1 : 다른 목적을 위한 차원 축소에는 tSNE가 적합하지 않습니다.

• t-SNE는 2차원 ~3차원으로 축소되는 것까지 유효하지만, 데이터의 차원이 3 차원 초과로 축소되는 경우에서 t-SNE이 어떻게 수행되는지는 분명하지 않습니다.
• 데이터를 2 차원 또는 3 차원으로 축소 할 때 t-SNE의 알고리즘은 두꺼운 꼬리 때문에 d > 3 차원으로 쉽게 Projection 시키는 건 좋지 않습니다.
• Student-t 분포의 고차원 공간에서 무거운 꼬리는 확률 질량의 상대적으로 큰 부분을 차지하게 됩니다.
• 데이터의 차원이 3보다 큰 차원으로 축소되어야 하는 작업의 경우, 1 이상의 자유도를 갖는 Student-t 분포가 더 적합 할 수 있습니다.

2. 약점 2 : 차원의 저주에 민감합니다.

• t-SNE는 데이터의 로컬 속성을 기반으로 데이터의 차원을 줄여주므로 t-SNE는 데이터의 고유한 차원의 저주에 민감합니다.
• 높은 고유 차원과 다양성을 갖는 기본 매니폴드가 있는 데이터 세트에서 t-SNE이 암묵적으로 가까운 이웃 사이의 유클리드 거리를 사용하여 만드는 매니폴드의 로컬 선형성 가정이 위반 될 수 있습니다.
• t-SNE가 매우 높은 고유 차원 (intrinsic dimensionality)을 갖는 데이터 세트에 적용되면 성공하지 못할 수도 있다. 예로 Meytlis and Sirovich (2007)의 최근 연구에 따르면 얼굴의 이미지 공간은 대략 100 차원이나 됩니다.

• Isomap 및 LLE와 같은 매니 폴드 학습자는 똑같은 문제를 겪고있다. 차원의 저주 문제를 (부분적으로) 해결할 수있는 방법은 아래와 같습니다.

  • Autoencoder과 같이 다양한 비선형 레이어에서 다양한 데이터의 매니폴드를 효율적으로 표현하는 모델에서 얻은 데이터 표현에 대해 t-SNE를 수행하는 것입니다.

  • 딥레이어 아키텍처는 복잡한 비선형 함수를 훨씬 단순한 방식으로 나타낼 수 있습니다.

  • Autoencoder가 t-SNE와 같은 로컬 메소드보다 더 잘 변화하는 매니 폴드를 더 잘 식별 할 수 있기 때문입니다. 예를 들어 autoencoder에 의해 생성된 데이터 표현에서 t-SNE를 수행하면 시각화의 품질을 향상시킬 수 있습니다.

  • 그러나 본질적으로 고차원적인 구조를 완전히 표현하는 것은 정의상 불가능하다.

3. 약점 3 : t-SNE 비용 함수의 Non - convexity

• 대부분의 최첨단 차원 축소 기술 (예 : classical scaling, Isomap, LLE)의 좋은 특성은 비용 함수의 볼록성의 특징이 있습니다.
• t-SNE의 주요 단점은 비용 함수가 볼록하지 않기때문에 여러 최적화 매개 변수를 선택해야 한다는 점이다. 그리고, 그에 따라 구성된 솔루션이 달라집니다.
• t-SNE가 맵 포인트의 초기 무작위 구성에서 실행될 때마다 다를 수 있으나, 다양한 최적화 매개 변수가 다양한 시각화 작업에 사용될 수 있음을 입증했으며 최적의 품질은 실행마다 크게 다르지 않음을 확인했습니다.

논문구현

본 논문 reproduction 과제에 있어서 구현을 해본 부분은 t-SNE 논문의 experiment 내용 중 MNIST Dataset에 대한 내용이다. 논문과 동일한 실험환경으로 셋팅했으며, 함수 최적화를 위해 함수만 구현하고 실제로 돌린 모델을 돌릴때는 sklearn 내장함수를 이용했다. 파라미터는 논문에 나온 파라미터값을 그대로 사용하였다. 논문과 마찬가지로 Isomap과 LLE 또한 적용하여 비교를 수행하였다. t-SNE의 베이스라인 코드는 아래 링크를 참고하여 구현하였다. (https://nlml.github.io/in-raw-numpy/in-raw-numpy-t-sne/)

기본 metric 연산 함수

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# neg-유클리디안 거리 함수(-|xi-xj|^2)
def neg_squared_euc_dists(X):
    sq_sum = np.square(np.linalg.norm(X, ord = 2, axis = 1))
    D = np.add(np.add(-2 * np.dot(X, X.T), sq_sum).T, sq_sum)
    return -D

# 거리를 확률값들로 변환해주는 함수
def calc_prob_matrix(distances, sigmas=None):
    if sigmas is not None:
        two_sig_sq = 2.0 * np.square(sigmas.reshape((-1, 1)))
        return scipy.special.softmax((distances / two_sig_sq), axis = 1)
    else:
        return scipy.special.softmax(distances, axis = 1)

# Perplexity 반환 함수
def perplexity(distances, sigma):
    probability_matrix = calc_prob_matrix(distances, sigma)
    Hp = -np.sum(probability_matrix * np.log2(probability_matrix), 1)
    return 2**Hp

# 예측값이 타겟값과 같아지도록 탐색을 반복하는 알고리즘
def binary_search(function, target, tol=1e-10, max_iter=10000, 
                  lower=1e-20, upper=1000.):
    
    for i in range(max_iter):
        guess = (lower + upper) / 2.
        value = function(guess)
        
        if value > target: upper = guess
        else:  lower = guess
            
        # break if target = prediction
        if np.abs(value - target) <= tol:
            break
            
    return guess

# 데이터로부터 얻은 거리 행렬의 각 행에 적합한 시그마 반환
def find_optimal_sigmas(distances, target_perplexity):
    sigmas = [] 
    for i in range(distances.shape[0]):
        # Perplexity calculation for one row
        function = lambda sigma:  perplexity(distances[i:i+1, :], np.array(sigma))
        # return correct sigmas
        correct_sigma = binary_search(function, target_perplexity)
        sigmas.append(correct_sigma)
    return np.array(sigmas)

논문에서 정의된 Equation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
*# Eauation 1 - p(j|i)*
def p_ji_prob(X, target_perplexity):
    distances = neg_squared_euc_dists(X)
    sigmas = find_optimal_sigmas(distances, target_perplexity)
    probability_matrix = calc_prob_matrix(distances, sigmas)
	  p_ji_output =(probability_matrix + probability_matrix.T) / (2.0 * probability_matrix.shape[0])
    return p_ji_output

# Equation 4 - q(ij)
def q_tsne(Y):
    distances = neg_squared_euc_dists(Y)
    inv_distances = np.power(1.0 - distances, -1)
    np.fill_diagonal(inv_distances, 0.)
    q_tsne = inv_distances / np.sum(inv_distances)
    return q_tsne, inv_distances

# Equation 5 - Gradient of Cost
def tsne_grad(P, Q, Y, inv_distances):
    pq_diff = P - Q  
    pq_expanded = np.expand_dims(pq_diff, 2) *#p(ij)-q(ij)*
    y_diffs = np.expand_dims(Y, 1) - np.expand_dims(Y, 0) *#y(i)-y(j)*
    distances_expanded = np.expand_dims(inv_distances, 2) *#(1+||yi-yj||^2)^(-1)*

    return 4. * (pq_expanded * y_diffs * distances_expanded).sum(1)

# Y 업데이트 함수
def estimate_sne(X, y, P, num_iters, q_function, gradient_function, learning_rate, momentum):
    
    Y = np.random.RandomState(1234).normal(0., 0.0001, [X.shape[0], 2])
    Y_m2 = Y.copy(); Y_m1 = Y.copy()
    
    *# Gradient Descent*
    for i in range(num_iters):
        Q, distances = q_function(Y)
        gradient = gradient_function(P, Q, Y, distances)

        *# Y Update*
        Y = Y - learning_rate * gradient
        Y += momentum * (Y_m1 - Y_m2)
        Y_m2 = Y_m1.copy()
        Y_m1 = Y.copy()
        
    return Y

논문 실험 구현 코드

1
2
3
4
5
6
7
8
9
10
11
12
# import libraries
from __future__ import print_function
import time
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_openml
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE, LocallyLinearEmbedding, Isomap
%matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns

1
2
3
4
5
6
7
8
9
10
11
12
13
# fetch data 
mnist = fetch_openml('mnist_784')
X = mnist.data / 255.0
y = mnist.target
print(X.shape, y.shape)

# make dataframe
feat_cols = [ 'pixel'+str(i) for i in range(X.shape[1]) ]
df = pd.DataFrame(X,columns=feat_cols)
df['y'] = y
df['label'] = df['y'].apply(lambda i: str(i))
X, y = None, None
print('Size of the dataframe: {}'.format(df.shape))

1
2
3
4
5
6
7
8
9
10
11
12
# 랜덤 시드 설정
np.random.seed(42)
rndperm = np.random.permutation(df.shape[0])

# 6000개 row sampling
N = 6000
df_subset = df.loc[rndperm[:N],:].copy()
data_subset = df_subset[feat_cols].values

# pca를 이용한 차원축소 (30차원)
pca = PCA(n_components=30)
pca_result = pca.fit_transform(data_subset)

1
2
3
4
# fit model
tsne_result = tsne.fit_transform(pca_result)
lle_result = lle.fit_transform(pca_result)
isomap_result = isomap.fit_transform(pca_result)

1
2
3
4
5
6
7
8
9
10
11
12
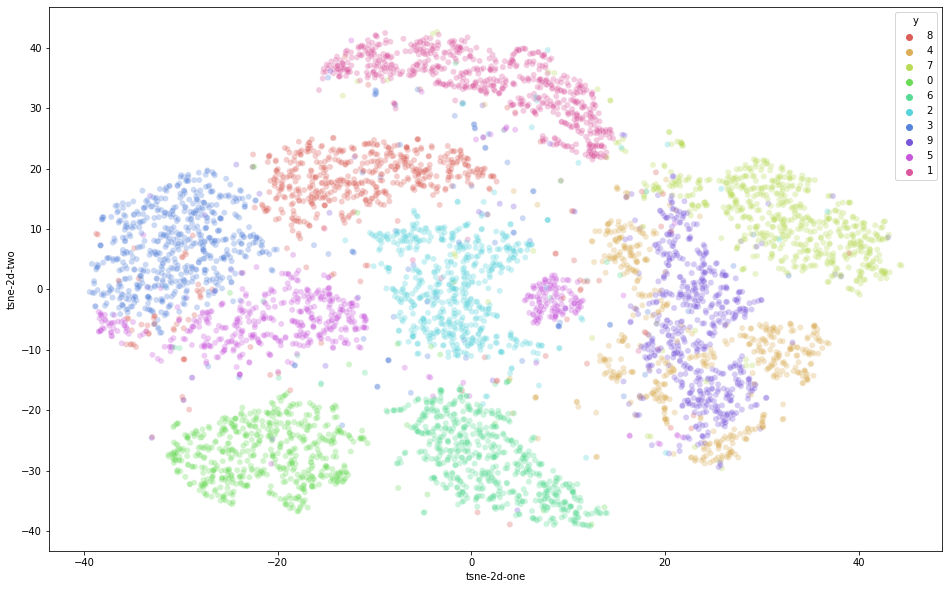
# visualize t-sne
df_subset['tsne-2d-one'] = tsne_result[:,0]
df_subset['tsne-2d-two'] = tsne_result[:,1]
plt.figure(figsize=(16,10))
sns.scatterplot(
    x="tsne-2d-one", y="tsne-2d-two",
    hue="y",
    palette=sns.color_palette("hls", 10),
    data=df_subset,
    legend="full",
    alpha=0.3
)

1
2
3
4
5
6
7
8
9
10
11
12
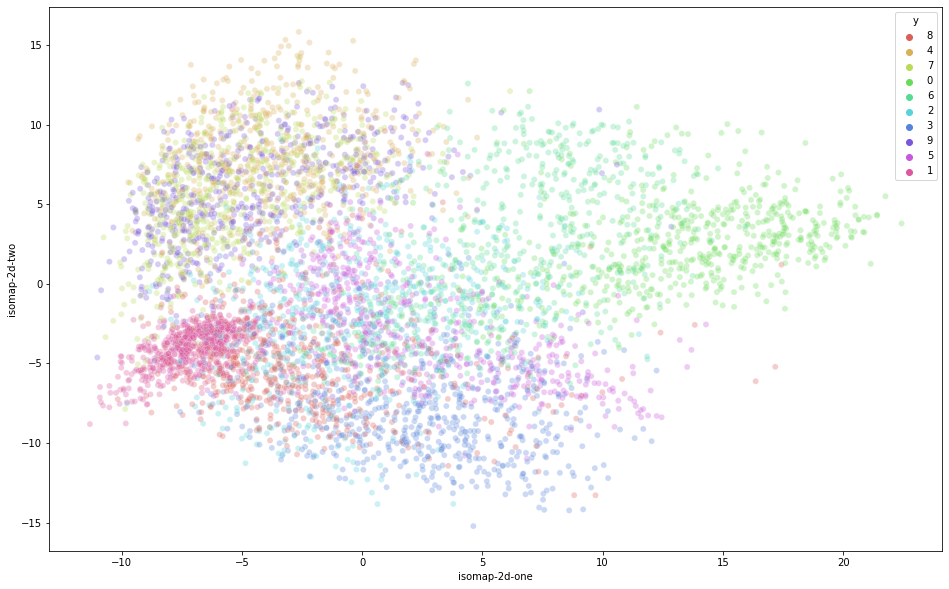
# visualize isomap
df_subset['isomap-2d-one'] = isomap_result[:,0]
df_subset['isomap-2d-two'] = isomap_result[:,1]
plt.figure(figsize=(16,10))
sns.scatterplot(
    x="isomap-2d-one", y="isomap-2d-two",
    hue="y",
    palette=sns.color_palette("hls", 10),
    data=df_subset,
    legend="full",
    alpha=0.3
)

1
2
3
4
5
6
7
8
9
10
11
12
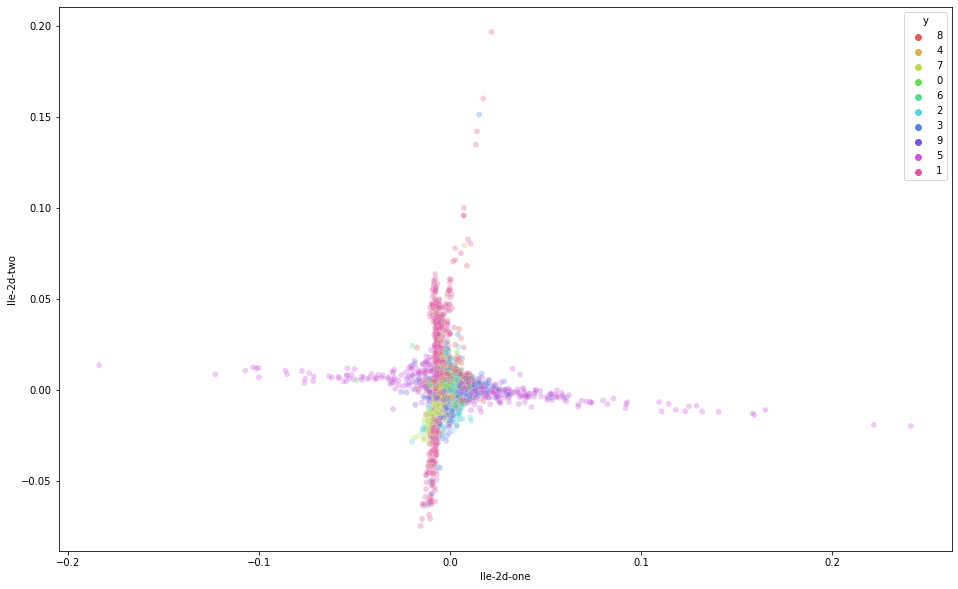
# visualize lle
df_subset['lle-2d-one'] = lle_result[:,0]
df_subset['lle-2d-two'] = lle_result[:,1]
plt.figure(figsize=(16,10))
sns.scatterplot(
    x="lle-2d-one", y="lle-2d-two",
    hue="y",
    palette=sns.color_palette("hls", 10),
    data=df_subset,
    legend="full",
    alpha=0.3
)

글을 마무리하며

• 이번 포스트에서는 논문을 읽고, 논문의 실험 환경과 동일하게 6000개의 MNIST 데이터를 이용해 분석을 수행해 보았습니다.
• 랜덤 시드로 추출한 6000개의 데이터라 완전히 데이터의 형태가 같지는 않지만, 확실히 비교 모델보다 t-SNE가 좀 더 2차원 상에 데이터를 정확히 구분해주는 것을 확인할 수 있었습니다.
• 본 논문에서는 MNIST 데이터 외에도 Olivetti faces, COIL-20 데이터 등을 사용하여 실험을 진행하였는데 구현 상에 차이가 없다고 판단하여 이를 생략하고 MNIST 데이터(6000개 추출) 실험만을 구현하고, 좀 더 논문을 깊게 파고 들려고 노력하였습니다.
• t-SNE는 현재도 고차원 데이터를 저차원에 표현할때 많이 쓰는 알고리즘으로, 이번 논문 정리 및 구현을 통해 추후 있을 연구에 도움이 될 것이라고 믿습니다.

긴 글 읽어주셔서 감사합니다 ^~^

• Previous
  [Paper Review] Transferring Inductive Bias Through Knowledge Distillation - (2/3)
• Next
  [개념] CPU, GPU, 그리고 GPU 원리